标签:operator bool 不能 组织者 ios rpe for 允许 不同的
【引子】
还记得 NOIP 2011 提高组 Day1 中的铺地毯吗?时光飞逝,光阴荏苒,三年过去了。组织者精心准备的颁奖典礼早已结束,留下的则是被人们踩过的地毯。
请你来解决类似于铺地毯的另一个问题。
【问题描述】
会场上有 n 个关键区域,不同的关键区域由 m 条无向地毯彼此连接。每条地毯可由三个整数 u、v、w 表示,其中 u 和 v 为地毯连接的两个关键区域编号,
w 为这条地毯的美丽度。由于颁奖典礼已经结束, 铺过的地毯不得不拆除。为了贯彻勤俭节约的原则,组织者被要求只能保留 K 条地毯,且保留的地毯构成的图中,任意可互相到达
的两点间只能有一种方式互相到达。换言之,组织者要求新图中不能有环。现在组织者求助你,想请你帮忙算出这 K 条地毯的美丽度之和最大为多少。
【输入格式】
第一行包含三个正整数 n、m、K。
接下来 m 行中每行包含三个正整数 u、v、w。
【输出格式】
只包含一个正整数,表示这 K 条地毯的美丽度之和的最大值。
【样例输入】
5 4 3
1 2 10
1 3 9
2 3 7
4 5 3
【样例输出】
22
【样例说明】
选择第 1、2、4 条地毯,美丽度之和为 10 + 9 + 3 = 22。
若选择第 1、2、3 条地毯,虽然美丽度之和可以达到 10 + 9 + 7 = 26,但这将导致关键区域 1、2、3 构成一个环,这是题目中不允许的。
【数据规模与约定】
所有测试点的数据规模如下:
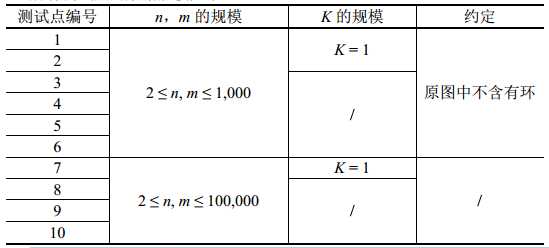
对于全部测试数据满足 1 ≤ K ≤ n-1,1 ≤ u≠v ≤ n,1 ≤ w ≤ 1,000。保证至少存在一种方案使得在原图中可以选出 K 条边,这 K 条边构成的新图无环。
裸的最大生成树。
#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> using namespace std; const int maxn=100000+5; inline int read() { int x=0,f=1; char ch=getchar(); while(ch<‘0‘||ch>‘9‘){if(ch==‘-‘) f=-1; ch=getchar();} while(ch>=‘0‘&&ch<=‘9‘){x=x*10+ch-‘0‘; ch=getchar();} return x*f; } int n,m,k,cnt,ans; int father[maxn]; struct edges { int u,v,w; bool operator < (const edges &j) const { return w>j.w; } }e[maxn]; inline int find(int x) { if(x!=father[x]) father[x]=find(father[x]); return father[x]; } int main() { freopen("carpet.in","r",stdin); freopen("carpet.out","w",stdout); n=read();m=read();k=read(); for(int i=1;i<=n;i++) father[i]=i; for(int i=1;i<=m;i++) { e[i].u=read(); e[i].v=read(); e[i].w=read(); } sort(e+1,e+m+1); for(int i=1;i<=m;i++) { int r1=find(e[i].u); int r2=find(e[i].v); if(r1!=r2) { father[r1]=r2; cnt++; ans+=e[i].w; } if(cnt==k) break; } printf("%d\n",ans); fclose(stdin); fclose(stdout); return 0; }
标签:operator bool 不能 组织者 ios rpe for 允许 不同的
原文地址:http://www.cnblogs.com/huihao/p/7454693.html