标签:好的 搜索 一个 http 曲线 无法 实现 最优 样本
1.概念
蒙特卡罗方法(随机取样法)是一种计算方法。原理是通过大量随机样本,去了解一个系统,进而得到所要计算的值。
2.两个应用例子
例子1:求π的值。
正方形内部有一个相切的圆,它们的面积之比是π/4。现在,在这个正方形内部,随机产生1000000个点(即1000000个坐标对 (x, y)),计算它们与中心点的距离,从而判断是否落在圆的内部。如果这些点均匀分布,那么圆内的点应该占到所有点的 π/4,因此将这个比值乘以4,就是π的值。

MATLAB实现:
N=1000000; %随机点的数目
x=rand(N,1); %rand 生成均匀分布的伪随机数。分布在(0~1)之间
y=rand(N,1); %矩阵的维数为N×1
count=0;
for i=1:N
if (x(i)^2+y(i)^2<=1)
count=count+1;
end
end
PI=4*count/N
例子2:计算积分
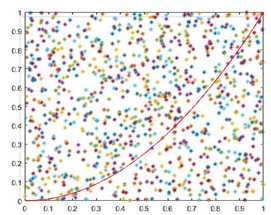
计算函数 y = x^2 在 [0, 1] 区间的积分,就是求出红色曲线下面的面积。这个函数在 (1,1) 点的取值为1,所以整个红色区域在一个面积为1的正方形里面。在该正方形内部,产生大量随机点,可以计算出有多少点落在红色区域(判断条件 y < x^2)。这个比重就是所要求的积分值。
MATLAB实现:
clear
clc
N=10000;
x=rand(N,1);
y=rand(N,1);
count=0;
for i=1:N
if (y(i)<=x(i)^2)
count=count+1;
end
end
result=count/N
3. 与拉斯维加斯方法的比较
(1)蒙特卡罗算法:假如筐里有100个苹果,让我每次闭眼拿1个,挑出最大的。于是我随机拿1个,再随机拿1个跟它比,留下大的,再随机拿1个……我每拿一次,留下的苹果都至少不比上次的小。拿的次数越多,挑出的苹果就越大,但我除非拿100次,否则无法肯定挑出了最大的。——尽量找好的,但不保证是最好的。
特点:采样越多,越近似最优解;
(2)拉斯维加斯方法:假如有一把锁,给我100把钥匙,只有1把是对的。于是我每次随机拿1把钥匙去试,打不开就再换1把。我试的次数越多,打开(最优解)的机会就越大,但在打开之前,那些错的钥匙都是没有用的。——尽量找最好的,但不保证能找到。
特点:采样越多,越有机会找到最优解。
4.更深度的应用
蒙特卡洛树搜索---深度学习,强化学习
标签:好的 搜索 一个 http 曲线 无法 实现 最优 样本
原文地址:http://www.cnblogs.com/youngsea/p/7457683.html