Luogu P3378 【模板】堆

标签：col   0ms   正整数   asc   元素   规模   维护   大于   格式   

题目描述

如题，初始小根堆为空，我们需要支持以下3种操作：

操作1： 1 x 表示将x插入到堆中

操作2： 2 输出该小根堆内的最小数

操作3： 3 删除该小根堆内的最小数

输入输出格式

输入格式：

第一行包含一个整数N，表示操作的个数

接下来N行，每行包含1个或2个正整数，表示三种操作，格式如下：

操作1： 1 x

操作2： 2

操作3： 3

输出格式：

包含若干行正整数，每行依次对应一个操作2的结果。

输入输出样例

5
1 2
1 5
2
3
2

2
5

说明

时空限制：1000ms,128M

数据规模：

对于30%的数据：N<=15

对于70%的数据：N<=10000

对于100%的数据：N<=1000000（注意是6个0。。。不过不要害怕，经过编者实测，堆是可以AC的）

样例说明：

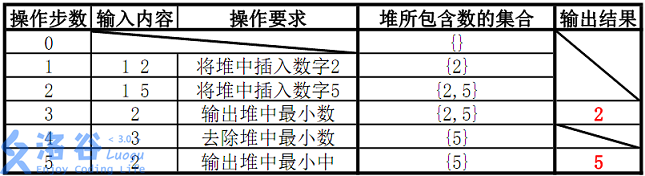
故输出为2、5

Solution

这道题需我们进行4步操作：插入、调整、查询和删除。

插入：

在插入时，只需将插入的数放在堆的最后一位，然后自下往上进行调整。

调整：

1.自下往上调整：

调整时，我们将当前节点与它的父亲节点相比，若小于父亲节点则这两点交换，并将它的父亲节点标为当前节点，直到达到根节点或大于父亲节点为止。这样，我们就能保证每一个节点都能大于其父亲节点，从而成功维护小根堆。

2.自上往下调整：

调整时我们将当前节点与它的两个孩子节点相比（若只有一个孩子节点则只与那个孩子节点比较），若大于较小的那个孩子节点则这两点交换，并将该孩子节点标为当前节点，直到到达叶子结点或小于较小的那个孩子节点为止。这样，选孩子节点中较小的那个与当前节点比较，若交换后它也比另一个孩子节点小，我们就能保证每一个节点都能大于其父亲节点，从而成功维护小根堆。

查询：

只需输出堆中的第一个元素（即根节点）就行啦！

删除：

删除时，只需将堆的最后一个节点的值赋给第一个节点，覆盖掉原来第一个节点的值，并将堆的节点数-1，代表删除堆的最后一个节点。

——————分隔不完全的分割线——————

pascal代码如下：

var n,m,i,j,k,l,min:longint;
a:array[0..2000000]of longint;//堆
begin
  readln(n);
  for m:=1 to n do
  begin
    read(l);
    if l=1 then//插入操作
    begin
      inc(k);
      read(a[k]);
      i:=k;
      while a[i]<a[i div 2] do//自下往上调整
      begin
        j:=a[i];
        a[i]:=a[i div 2];
        a[i div 2]:=j;
        i:=i div 2;
      end;
    end
    else
    if l=2 then//查询操作
    writeln(a[1])
    else
    begin//删除操作
      a[1]:=a[k];
      dec(k);
      i:=1;
      if (a[i*2]<a[i*2+1])or(i*2=k) then//比较两个孩子节点的值，取小的那一个与该节点比较
      min:=i*2
      else
      min:=i*2+1;
      while (min<=k)and(a[i]>a[min]) do//自上往下调整
      begin
        j:=a[i];
        a[i]:=a[min];
        a[min]:=j;
        i:=min;
        if (a[i*2]<a[i*2+1])or(i*2=k) then
        min:=i*2
        else
        min:=i*2+1;
      end;
    end;
  end;
end.

Luogu P3378 【模板】堆

标签：col   0ms   正整数   asc   元素   规模   维护   大于   格式   

原文地址：http://www.cnblogs.com/qbwhtc/p/7465179.html