标签:blog http os io ar strong for 2014 art
在讲解反素数之前,我们先来看反素数的概念。
反素数的定义:对于任何正整数



数


从反素数的定义中可以看出两个性质:
(1)一个反素数的所有质因子必然是从2开始的连续若干个质数,因为反素数是保证约数个数为

(2)同样的道理,如果
在ACM竞赛中,最常见的问题如下:
(1)给定一个数


(2)求出
从上面的性质中可以看出,我们要求最小的

以前我们求一个数的所有因子也是用搜索,比如

以
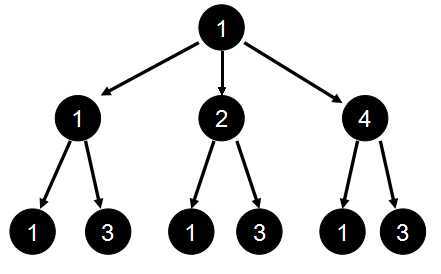
再看一道例题:
题意:给一个数

#include <iostream>
#include <string.h>
#include <stdio.h>
using namespace std;
typedef unsigned long long ULL;
const ULL INF = ~0ULL;
int p[16] = {2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53};
int n;
ULL ans;
void dfs(int dept,ULL tmp,int num)
{
if(num > n) return;
if(num == n && ans > tmp) ans = tmp;
for(int i=1;i<=63;i++)
{
if(ans / p[dept] < tmp) break;
dfs(dept+1,tmp *= p[dept],num*(i+1));
}
}
int main()
{
while(cin>>n)
{
ans = INF;
dfs(0,1,1);
cout<<ans<<endl;
}
return 0;
}
-------------以上转自http://blog.csdn.net/ACdreamers/article/details/25049767----------
我自己想说一下对例题代码的理解
代码主要部分是
int p[16] = {2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53};
int n;
ULL ans;
void dfs(int dept,ULL tmp,int num) //其实此处DFS即是枚举。i的次数递增,即是对应
//p[dept]的指数的增加。深度dept即是第几个素数。63次方已是
//足够大了。枚举指数来看其约数的个数。
{
if(num > n) return;
if(num == n && ans > tmp) ans = tmp;
for(int i=1;i<=63;i++)
{
if(ans / p[dept] < tmp) break;
dfs(dept+1,tmp *= p[dept],num*(i+1));
}
}
int main()
{
while(cin>>n)
{
..................
dfs(0,1,1);
.................
}
return 0;
}
ZOJ 2562
紧接着,我自己就做了这一题
#include <iostream>
#include <cstdio>
#include <algorithm>
#define LL long long
using namespace std;
LL p[16] = {2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53};
LL ans,n,c;
void solve(int dep,LL tmp, LL num){
if(tmp>n) return ;
if(num>c||(num==c)&&tmp<ans){
ans=tmp;
c=num;
}
for(LL i=1;i<=60;i++){
if(tmp*p[dep]>n) break;
solve(dep+1,tmp*p[dep],num*(i+1));
tmp*=p[dep];
}
}
int main(){
while(scanf("%lld",&n)!=EOF){
c=0;
ans=(1<<60);
solve(0,1,1);
printf("%lld\n",ans);
}
return 0;
}
标签:blog http os io ar strong for 2014 art
原文地址:http://www.cnblogs.com/jie-dcai/p/3959468.html