标签:整数 机智 bsp signed ima 多少 std pow height
发布时间: 2015年9月6日 15:18 最后更新: 2016年6月26日 12:10 时间限制: 1000ms 内存限制: 256M
机智无比的G神今天完成了一天的任务,实在是无聊的紧,拿起一支笔在纸上画起了三角形,边长为1, 2, 3,.........
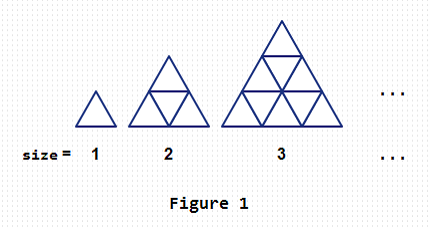
即使是无聊到这种程度,G神发达的大脑也在不停的思考,从顶部的点到沿着所画出的边到达底边的方案有多少种呢。
结果可能比较大, 结果对1000003取余。
例如,边长为2的情况如下所示:
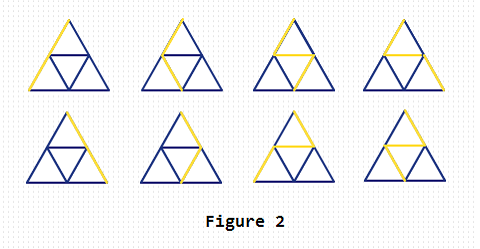
第一行有一个整数 T (1 <= T <= 1000) ,是三角形的个数。
接下来T行,每行一个整数 N (1 <= N <= 10^18),代表三角形边长。
输出T行,每行代表方案数,结果对1000003取余。
3 1 2 3
2 8 48
一道找规律好题?
先给出答案通项吧。
\( ans_n = n! \times 2^n \)
再来给出解释——
我们可以把其看作一个DP,有
\( ans_n = 2n \times ans_{n-1} \)
考虑到达n-1的底层的每个方案,在其基础上有多少方案到达n的底层呢?
不难发现,对于一个到达n-1的底层某个固定点的方案,到n的底层中间的n-1个点(除了最左和最右点),都有且仅有两种方案,即最后一步是↘或最后一步是↙。而最左和最右都只有一种方案,加起来就是\( 2 \times (n-1) + 1 + 1 = 2 \times n \)。
然后,考虑编程问题,n!可以暴力递推前1000002项,而当\( n \geq 1000003 \)时,n!在模意义一定为0。至于\( 2^n \),写个快速幂就好了。
1 #include <cstdio> 2 3 #define int long long 4 5 const int mxn = 1000010; 6 const int mod = 1000003; 7 8 int n, cas, fac[mxn]; 9 10 inline int pow(int a, int b) { 11 int r = 1; 12 for (; b; b >>= 1) { 13 if (b & 1) 14 r = r * a % mod; 15 a = a * a % mod; 16 } 17 return r; 18 } 19 20 signed main() { 21 fac[0] = 1; 22 for (int i = 1; i < mod; ++i) 23 fac[i] = i * fac[i - 1] % mod; 24 for (scanf("%lld", &cas); cas--; ) 25 if (scanf("%lld", &n), n < mod) 26 printf("%lld\n", fac[n] * pow(2, n) % mod); 27 else 28 puts("0"); 29 }
标签:整数 机智 bsp signed ima 多少 std pow height
原文地址:http://www.cnblogs.com/kenro/p/7465412.html