标签:random 二分查找 rand 排序 大小 png 序列 key 记录
因为别人问了我一个问题当时一两分钟没想上来,后面搜索了下,找到了一个文章写的很全。搬过来记一下。原问题是想设计一个算法在一个集合中随便选一个数,但是选出来这个数的概率要和这个数的大小成正比。也就是说希望越大的数被大概率的选出来。
这个问题更清晰点儿描述是,有一组数字,他们都带有不同的权重,现在要从中“随机”抽一个数字,但是抽到某个数字的概率要正比于他的权重。假设这个集合中的元素和其对应权重为{‘A’:50,‘B’:10,‘C’:100,‘D’:3,‘E’:60,‘F’:25}。
方法一
如果随机选的话,在一个list中出现的次数多被选中的概率就会大。所以可以按照权重组合一个list,在这个list中A有50个,B有10个,C有100个,等等。有了list之后,从中随机选一个。这样选取的时间负责度是O(1)。但是如果数字很多,权重又很大的话,那么空间负责度会很高。
import random data = {‘A‘: 50, ‘B‘: 10, ‘C‘: 100, ‘D‘: 3, ‘E‘: 60, ‘F‘: 25} value_list = [] for key, value in data.items(): value_list += value*[key] pick_value = random.choice(value_list)
进行100万次实验,计数每个字母被选中的次数。结果如下图所示
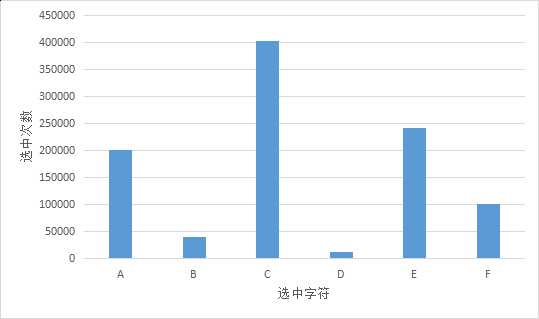
可以看出多次实验的结果,每个字符选中的次数确实与权重成正比。
方法二(常用)
对每个元素的权重进行加和记为sum,在1到sum之间随机选一个数。之后遍历整个集合,统计遍历到的项的权重之和,如果大于sum,则选择这个数。该方法需要遍历集合,时间复杂度为O(n)
import random data = {‘A‘: 50, ‘B‘: 10, ‘C‘: 100, ‘D‘: 3, ‘E‘: 60, ‘F‘: 25} value_sum = sum(data.values()) for i in range(1000000): t = random.randint(0, value_sum - 1) for key, value in data.items(): t -= value if t < 0: pick_value = key break
多次实验统计被选中的元素的次数如下图
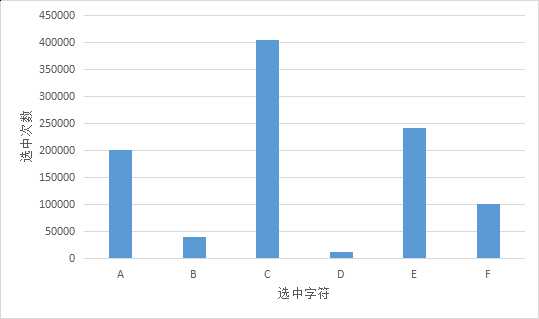
方法三
上面方法最坏的情况是遍历完所有的元素,但是如果权重大的元素能够先被遍历的话可以减少遍历次数。基于此,可以先对元素按照权重排序。但是这样排序的话也会比较花时间。可以计算一个前项和序列,记录到每一项时的权重是多少。然后随机生成一个数,可以用二分查找找这个数对应的索引,也就可以找到对应的元素。但是这样就要求数据不能存成字典,因为字典的遍历是无序的。
import bisect import random data = {‘A‘: 50, ‘B‘: 10, ‘C‘: 100, ‘D‘: 3, ‘E‘: 60, ‘F‘: 25} key_list = list(data.keys()) value_list = [data[key] for key in key_list] prefix_sum = [] tmp_sum = 0 for value in value_list: tmp_sum += value prefix_sum.append(tmp_sum) t = random.randint(0, tmp_sum - 1) pick_value = key_list[bisect.bisect_right(prefix_sum, t)]
同样统计结果如下
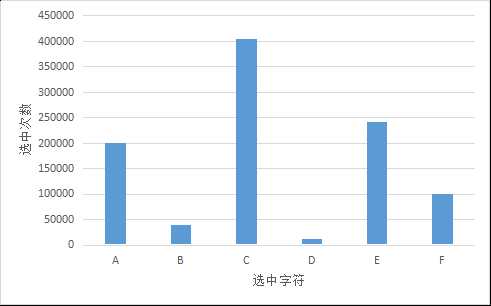
参考:
【1】http://www.cnblogs.com/zywscq/p/5469661.html
标签:random 二分查找 rand 排序 大小 png 序列 key 记录
原文地址:http://www.cnblogs.com/bhqmmachinelearning/p/7466546.html