对于A星/Astar/A*算法的一些理解

　　A星算法是经常利用到搜寻最短路径的算法，而相对于各种spfa，dijkstra等最短路算法，其最大的优势就是以一种贪心式的方法来逼近最优值，而非像spfa，dijkstra算法的较为盲目的搜索。

　　虽然可能在特殊设计出来的图上效率会与spfa，dijkstra相比较低，但是随机生成的图中其效率可以远远高于最短路径算法。

注：上图左边为dijkstra搜索时覆盖的点，右边为A*算法搜索时覆盖的点。

从上面图片就可以容易看出dijkstra算法所需要搜索范围高于A*算法的搜索一个数量级以上。

 function A*(start,goal)
     closedset := the empty set                 //已经被估算的节点集合    
     openset := set containing the initial node //将要被估算的节点集合
     came_from := empty map
     g_score[start] := 0                        //g(n)
     h_score[start] := heuristic_estimate_of_distance(start, goal)    //h(n)
     f_score[start] := h_score[start]            //f(n)=h(n)+g(n)，由于g(n)=0，所以……
     while openset is not empty                 //当将被估算的节点存在时，执行
         x := the node in openset having the lowest f_score[] value   //取x为将被估算的节点中f(x)最小的
         if x = goal            //若x为终点，执行
             return reconstruct_path(came_from,goal)   //返回到x的最佳路径
         remove x from openset      //将x节点从将被估算的节点中删除
         add x to closedset      //将x节点插入已经被估算的节点
         foreach y in neighbor_nodes(x)  //对于节点x附近的任意节点y，执行
             if y in closedset           //若y已被估值，跳过
                 continue
             tentative_g_score := g_score[x] + dist_between(x,y)    //从起点到节点y的距离
 
             if y not in openset          //若y不是将被估算的节点
                 add y to openset         //将y插入将被估算的节点中
                 tentative_is_better := true     
             elseif tentative_g_score < g_score[y]         //如果y的估值小于y的实际距离
                 tentative_is_better := true         //暂时判断为更好
             else
                 tentative_is_better := false           //否则判断为更差
             if tentative_is_better = true            //如果判断为更好
                 came_from[y] := x                  //将y设为x的子节点
                 g_score[y] := tentative_g_score
                 h_score[y] := heuristic_estimate_of_distance(y, goal)
                 f_score[y] := g_score[y] + h_score[y]
     return failure
 
 function reconstruct_path(came_from,current_node)
     if came_from[current_node] is set
         p = reconstruct_path(came_from,came_from[current_node])
         return (p + current_node)
     else
         return current_node

对于普通的A*算法来说，凭着贪心都能够贪到一个不错的结果，而这里希望讨论的是贪心的正确性。

　　　　这是从v_JULY_v 结构之法_算法之道中提到的 A*搜索算法。（值得一看）

对于1，2，3点都是应该能明白，而第4点也是最重要的一点吧，入门者需要思考后才能明白。然而在网上却很难找到对其直白的表述。

对于一个图来说，只要保证h(n)<=h*(n)，就能使得搜出的每一个点都能保证最优。

通常广搜本质上便是每次距离+1进行搜索，因而第一次搜到的点距离一定是最短的。事实上广搜每个点h值相当于0，故恒<=h*。

（无法用严谨的语言进行严格证明，但证明要点应该都在，若有人找到严格证明还望告知我，多谢啦！）

（广搜需要开一个队列，其中openset表示队列中未搜索的部分，而closeset表示队列中已搜索的部分）

　　设搜索到点T的最短路径，当前搜索到点S，g(S)值为起点到S的最短路径长度=g*(S)，h(S)为在点S处预估到T的距离<=S到T的实际最短距离h*(S)。

　　现在说明搜索到的第一个点T时，即第一次在openset队列遇到点T时，g(T)=g*(T)为S到T的最短距离而h(T)<=h*(T)=0。

　　假设搜索中第一次遇到T，说明已经找到一条路径通向T，然而此时这条路径未必是最短路径，此时，我们假设这条路径的长度为g1(T)，则有g1(T)>=g*(T)，将其加入优先队列openset，其f1(T)=g1(T)+h1(T)=g1(T)+0=g1(T)>=g*(T)。故在openset队列访问到T之前，所f<f1的点集K均会先访问到。

　　接下来只需说明所有最短路径上的所有点∈K，因为所有点A有h(A)<h*(A)，故路径上的f(A)=g(A)+h(A)=g*(A)+h(A)<g*(T)+h*(T)=g*(T)<=g1(T)=f1(T)，故所有最短路径上的点都会在第一次在openset中遇到T之前搜到，且这些点进入优先队列openset都会在点T之前。

　　因此，在openset访问到T之前，最短路径上的点会先访问并且更新T的g(T)使得，g(T)不断向下逼近直到与g*(T)相同。

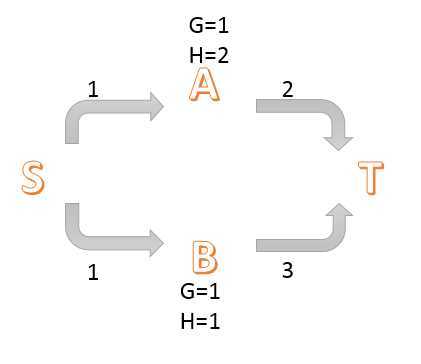
首先加入点A，B，并且在优先队列之前B点会在A点之前，先搜索B，而后加入T（g=4 h=0）排在A点之后，而后搜索A点，再更新T（g=3 h=0），算法结束。

可以看出，即使h(A)与A到T的最短距离大小比不同，依然能保证正确性，即只要保证h(A)<h*(A)即可搜出正确解。

而若实际上一般有h(A)=A到T点的最短距离，应该使得h(A)=2 h(B)=3，这样会使搜索效率提高。

此外，从上述简要证明可以看出，当估价函数h<=h*，让h尽可能接近h*，或者让h的单调性趋向于h*，均能够使得A*搜索速度得到快速提升。

而h>h*时，A*搜索速度很快，但不保证能够找到最短路径，但设计得当就能找到较短路径。

無障礙
有障礙