标签:style blog http io ar 2014 sp 代码 log
方法三:因为N*M的取值就是1,10,11,100,101,110,111,......所以直接在这个空间搜索,这是对方法一的改进。搜索这个序列直到找到一个能被N整除的数,它就是N*M,然后可计算出M。例如N=3时,搜索树如下:
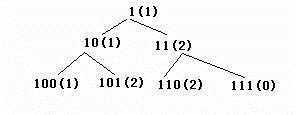
上图中括号内表示模3的余数。括号外表示被搜索的数。左子树表示0,右子树表示1.上图中搜索到第二层(根是第0层)时遇到111,它模3余数为0.所以N*M=111, M=111/3=37。
方法四:对方法三的改进。将方法三的搜索空间按模N余数分类,使得搜索时间和空间都由原来的指数级降到了O(N)。改进的原理:假设当前正在搜索由0,1组成的K位十进制数,这样的K位十进制数共有2^k个。假设其中有两个数X、Y,它们模N同余,那么在搜索由0、1组成的K+1位十进制数时,X和Y会被扩展出四个数:10X, 10X+1, 10Y, 10Y+1。因为X和Y同余(同余完全可以看作相等),所以10X与10Y同余,10X+1与10Y+1同余。也就是说由Y扩展出来的子树和由X扩展产生出来的子树产生完全相同的余数,如果X比Y小,那么Y肯定不是满足要求的最小的数,所以Y这棵子树可以被剪掉。这样,2^K个数按照模N余数分类,每类中只保留最小的那个数以供扩展。原来在这一层需要搜索2^K个数,现在只需要搜索O(N)个数。例如,当N=9时,第0层是1(1),
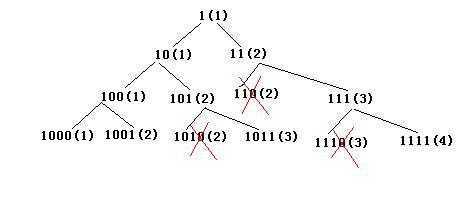
如上图所示,第2层的110,第三层的1010、1110都因为同一层有和它同余且更小的数而被剪掉(101和110余数都是2,但前者更小)。如果按照方法三搜索,第三层本来应该有8个结点,但现在只有4个结点。
方法三的源代码:
// 解法三(1):广度优先搜索
#define _CRT_SECURE_NO_WARNINGS 1
#include <cstdio>
#include <queue>
using namespace std;
int main() {
int N;
while(scanf("%d", &N) != EOF) {
queue<int> q;
q.push(1);
//从小到大找,因此首先找到的就是所要求的数
while(!q.empty()) {
int t = q.front();
q.pop();
if(t % N == 0) {
printf("n = %d, m = %d, n*m = %d/n", N, t/N, t);
break;
}
q.push(t * 10);
q.push(t * 10 + 1);
}
}
return 0;
}
方法四源代码:
// 解法四:将搜索空间分过类的广度搜索,这样空间占用是O(N)而不是
// 指数级。分类的原则是按照模N的余数分类
#define _CRT_SECURE_NO_WARNINGS 1
#include <cstdio>
#include <bitset>
#include <vector>
#include <queue>
using namespace std;
struct QNode {
int v, r; // v is 数值, r is 余数
QNode(int vv, int rr): v(vv), r(rr) {}
QNode(): v(0), r(0) {}
};
int main() {
int N;
while(scanf("%d", &N) != EOF) {
//bitset<N> bn;
queue<QNode> q;
q.push(QNode(1, 1));
while(!q.empty()) {
//bn.reset();
vector<bool> bn(N, false);
int s = q.size();
while(s--) {
QNode t = q.front();
if(t.r == 0) {
printf("n = %d, m = %d, n*m = %d/n", N, t.v/N, t.v);
goto ok;
}
q.pop();
//如果没有找到,那么说明还需要继续深入下一层。由于是从小到大进入下一层的,那么首//先找到的就是最小的。这里找的是对应0-N之间特定余数的节点值。
if(!bn[t.r * 10 % N]) {
bn[t.r * 10 % N] = true;
q.push(QNode(t.v * 10, t.r * 10 % N));
}
if(!bn[(t.r * 10 + 1) % N]) {
bn[(t.r * 10 + 1) % N] = true;
q.push(QNode(t.v * 10 + 1, (t.r * 10 + 1) % N));
}
}
}
ok:;
}
return 0;
}
标签:style blog http io ar 2014 sp 代码 log
原文地址:http://www.cnblogs.com/notlate/p/3959827.html