标签：class numpy 性问题 nbsp pre 一个 pytho 分离 image
一.感知机概述
感知机适用于：线性可分的数据，用于二分类
目的：找到分离超平面，完全分离不同的类
感知机公式：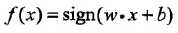
，一元多维的函数
感知机学习策略：通过求min(所有误分类点到超平面距离)，即损失函数，来确定权重和偏置
求解方法：梯度下降法
求解步骤：1.初始化权重和偏置
2.任选点（x,y）
3.若yi*(w*x+b)<=0,则更新w(new)=w(old)+eta*yi*xi,b(new)=b(old)+eta*yi ,其中0<eta<=1(这里通常我们令eta=1)
迭代收敛说明：Novikoff定理证明出误分类次数是有上界的，经有限次搜索可以找到分离超平面，感知机因初始值的选择有很多解。
下面是具体代码实现：
#感知机处理线性可分数据
import numpy as np
import random
import matplotlib.pyplot as plt
def getdata(num):#生成间隔大些的数据，需要输入数据量
xdata=[]
for i in range(num):
idata=[random.randint(0,20),random.randint(0,20)]
if sum(idata)>=20:
idata=[i+5 for i in idata]
if not idata in xdata:
xdata.append(idata)
ydata=[1 if sum(i)>=20 else -1 for i in xdata]
return xdata,ydata
def per(xdata,ydata,w,b):#求解w,b
while any([ydata[i]*(w[0]*xdata[i][0]+w[1]*xdata[i][1]+b)<=0 for i in range(len(xdata))]):
for i in range(len(xdata)):
while ydata[i]*(w[0]*xdata[i][0]+w[1]*xdata[i][1]+b)<=0:
w=[w[j]+ydata[i]*xdata[i][j] for j in range(2)]
b=b+ydata[i]
return w,b
def pic(w=[0,0],b=0,num=100):#画图
xdata, ydata = getdata(num)
xdata1 = [i[0] for i in xdata]
xdata2 = [i[1] for i in xdata]
plt.scatter(xdata1, xdata2, c=["r" if i == 1 else "b" for i in ydata],s=5)
plot_x = [1, 25]
w,b=per(xdata,ydata,w,b)
plot_y = [(-1) * (b + w[0] * plot_x[0]) / w[1], (-1) * (b + w[0] * plot_x[1]) / w[1]]
plt.plot(plot_x, plot_y)
效果如图所示：
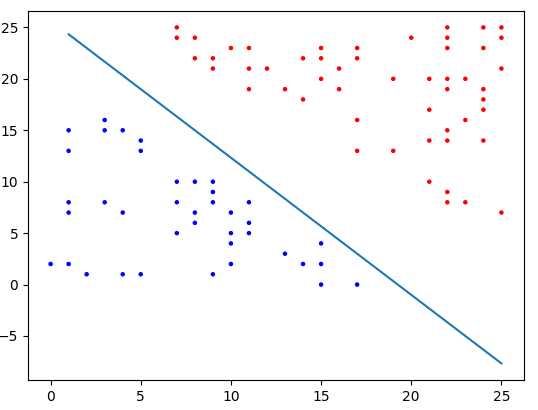
二.证明感知机不能处理异或问题
对于异或问题：
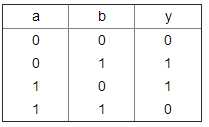
首先，我们假设异或问题是线性可分的，则有：
三，利用感知机处理异或问题
虽然感知机不能直接用来处理异或问题，但是我们可以通过激活函数来实现非线性问题的分类
这里我受到adaboost的启发，即多个弱分类器组合成为一个强分类器，我们可以如下构造：
下面是代码实现：
#处理线性不可分数据，异或
import numpy as np
xdata=[[0,0,0,1],[0,1,1,1],[1,0,1,1],[1,1,1,0]]#初始化数据
ydata=[-1,1,1,-1]#初始化数据
def per(xdata,ydata,w=[0,0,0,0],b=0):#求解w,b
while any([ydata[i]*(w[0]*xdata[i][0]+w[1]*xdata[i][1]+w[2]*xdata[i][2]+w[3]*xdata[i][3]+b)<=0 for i in range(len(xdata))]):
for i in range(len(xdata)):
while ydata[i]*(w[0]*xdata[i][0]+w[1]*xdata[i][1]+w[2]*xdata[i][2]+w[3]*xdata[i][3]+b)<=0:
w=[w[j]+ydata[i]*xdata[i][j] for j in range(4)]
b=b+ydata[i]
return w,b
结果为：
([-2, -1, 4, 3], -4)
标签：class numpy 性问题 nbsp pre 一个 pytho 分离 image
原文地址：http://www.cnblogs.com/danning13/p/7476660.html
