标签:方差 攻击 lan 防止 分类器 nal src cross 集中
在机器学习中,我们用训练数据集去训练(学习)一个model(模型),通常的做法是定义一个Loss function(误差函数),通过将这个Loss(或者叫error)的最小化过程,来提高模型的性能(performance)。然而我们学习一个模型的目的是为了解决实际的问题(或者说是训练数据集这个领域(field)中的一般化问题),单纯地将训练数据集的loss最小化,并不能保证在解决更一般的问题时模型仍然是最优,甚至不能保证模型是可用的。这个训练数据集的loss与一般化的数据集的loss之间的差异就叫做generalization error=bias+variance。
作者:路小墨
链接:https://www.zhihu.com/question/27068705/answer/82132134
来源:知乎
著作权归作者所有,转载请联系作者获得授权。
Bias反映的是模型在样本上的输出与真实值之间的误差,即模型本身的精准度,即算法本身的拟合能力
Variance反映的是模型每一次输出结果与模型输出期望之间的误差,即模型的稳定性。反应预测的波动情况。
这就简单了,就不是你想要的真正数据,你可以想象为来破坏你实验的元凶和造成你可能过拟合的原因之一,至于为什么是过拟合的原因,因为模型过度追求Low Bias会导致训练过度,对测试集判断表现优秀,导致噪声点也被拟合进去了
想象你开着一架黑鹰直升机,得到命令攻击地面上一只敌军部队,于是你连打数十梭子,结果有一下几种情况:
1.子弹基本上都打在队伍经过的一棵树上了,连在那棵树旁边等兔子的人都毫发无损,这就是方差小(子弹打得很集中),偏差大(跟目的相距甚远)。
2.子弹打在了树上,石头上,树旁边等兔子的人身上,花花草草也都中弹,但是敌军安然无恙,这就是方差大(子弹到处都是),偏差大(同1)。
3.子弹打死了一部分敌军,但是也打偏了些打到花花草草了,这就是方差大(子弹不集中),偏差小(已经在目标周围了)。
4.子弹一颗没浪费,每一颗都打死一个敌军,跟抗战剧里的八路军一样,这就是方差小(子弹全部都集中在一个位置),偏差小(子弹集中的位置正是它应该射向的位置)。
作者:刑无刀
链接:https://www.zhihu.com/question/20448464/answer/24397161
来源:知乎
著作权归作者所有,转载请联系作者获得授权。
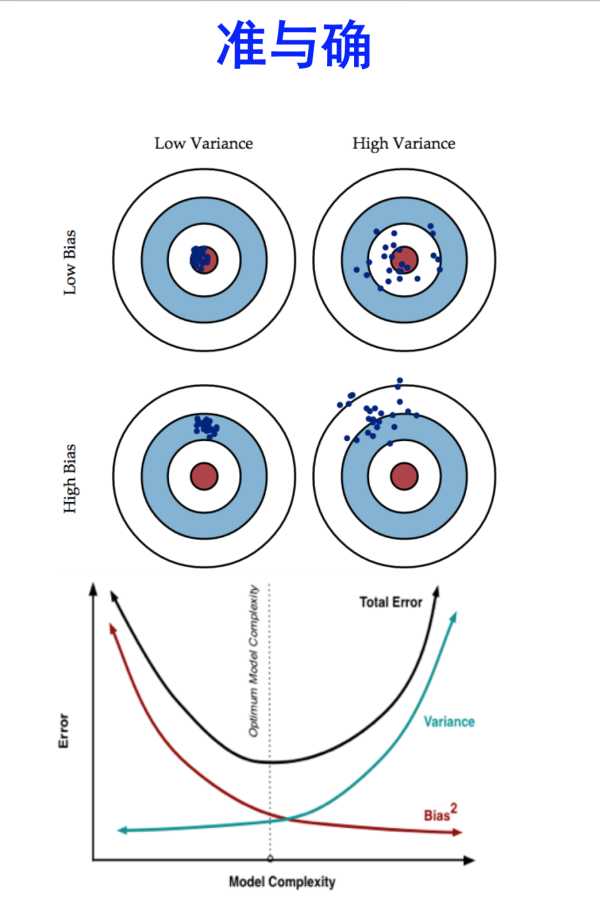
-再来个射箭问题:假设你在射箭,红星是你的目标,以下是你的射箭结果
https://www.zhihu.com/question/27068705
这里写图片描述
作者:Jason Gu
链接:https://www.zhihu.com/question/20448464
来源:知乎
著作权归作者所有,转载请联系作者获得授权。
分析:
我们可以看到,在Low Variance的一列,数据分布是非常集中的,恩,小伙子,你的稳定性很好,方差很小,表现的很聚集。而第二列就是High Variance的一列,机智的你可能一下就看出来了,没错,飘来飘去的,非常不稳定!
看下Low Bias这一行,命中红心的次数很多对不对,说明你还是有准头的,至少偏差不算大,我要是裁判,我就不管你没射中几只箭飘到哪去了(方差大,不集中),毕竟我看的是命中了多少(准确度),而High Bias这一行,明显可以看出一支箭都没射中,表现很差,偏离目标好远,负分滚粗!
综合起来看,我们需要的模型最好是两个L,又准确又稳定,妥妥的,但是,这个在现实模型中是不会存在的。你只能权衡着来
过拟合,也就是我对训练样本能够百分百命中了,超级拟合了,但是测试时候就掉链子,拟合很差,也就是我们说的泛化性能不好的问题,所以如果太追求在训练集上的完美而采用一个很复杂的模型,会使得模型把训练集里面的噪声都当成了真实的数据分布特征,从而得到错误的数据分布估计。
一句话,过拟合会出现高方差问题
欠拟合:训练样本太少,导致模型就不足以刻画数据分布了,体现为连在训练集上的错误率都很高的现象。
一句话,欠拟合会出现高偏差问题
避免欠拟合(刻画不够)
避免过拟合(刻画太细,泛化太差)
交叉验证方法
更多方法详解请看@一只鸟的天空--机器学习中防止过拟合的处理方法
1.交叉验证,这是仅使用训练集衡量模型性能的一个方便技术,不用建模最后才使用测试集
2.Cross-validation 是为了有效的估测 generalization error(泛化误差) 所设计的实验方法,而generalization error=bias+variance
首先:bias和variance分别从两个方面来描述了我们学习到的模型与真实模型之间的差距。Bias是 “用所有可能的训练数据集训练出的所有模型的输出的平均值” 与 “真实模型”的输出值之间的差异;Variance则是“不同的训练数据集训练出的模型”的输出值之间的差异。
作者:路小墨
链接:https://www.zhihu.com/question/27068705/answer/82132134
来源:知乎
著作权归作者所有,转载请联系作者获得授权。
可以发现,怎么来平衡Bias和Variance则成了我们最大的任务了,也就是怎么合理的评估自己模型呢?我们由此提出了交叉验证的思想,以K-fold Cross Validation(记为K-CV)为例,基本思想如下:(其他更多方法请看@bigdataage --交叉验证(Cross-Validation))
将原始数据分成K组(一般是均分),将每个子集数据分别做一次验证集,其余的K-1组子集数据作为训练集,这样会得到K个模型,用这K个模型最终的验证集的分类准确率的平均数作为此K-CV下分类器的性能指标.K一般大于等于2,实际操作时一般从3开始取,只有在原始数据集合数据量小的时候才会尝试取2. 而K-CV 的实验共需要建立 k 个models,并计算 k 次 test sets 的平均辨识率。在实作上,k 要够大才能使各回合中的 训练样本数够多,一般而言 k=10 (作为一个经验参数)算是相当足够了。
看不清上面的就来一幅更简单的
每次的training_set 红色, validation_set白色 ,也就是说k=5的情况了
注意:交叉验证使用的仅仅是训练集!!根本没测试集什么事!很多博客都在误导!
这也就解决了上面刚开始说的Variance(不同训练集产生的差异),Bias(所有data训练结果的平均值)这两大问题了!因为交叉验证思想集合了这两大痛点,能够更好的评估模型好坏!
说白了,就是你需要用下交叉验证去试下你的算法是否精度够好,够稳定!你不能说你在某个数据集上表现好就可以,你做的模型是要放在整个数据集上来看的!毕竟泛化能力才是机器学习解决的核心
下面解释一下Bias、Variance和k-fold的关系:k-fold交叉验证常用来确定不同类型的模型(线性、指数等)哪一种更好,为了减少数据划分对模型评价的影响,最终选出来的模型类型(线性、指数等)是k次建模的误差平均值最小的模型。当k较大时,经过更多次数的平均可以学习得到更符合真实数据分布的模型,Bias就小了,但是这样一来模型就更加拟合训练数据集,再去测试集上预测的时候预测误差的期望值就变大了,从而Variance就大了;反之,k较小时模型不会过度拟合训练数据,从而Bias较大,但是正因为没有过度拟合训练数据,Variance也较小。
作者:TANGent
链接:https://www.zhihu.com/question/27068705/answer/35286205
来源:知乎
著作权归作者所有,转载请联系作者获得授权。
@知乎--机器学习中的Bias(偏差),Error(误差),和Variance(方差)有什么区别和联系?
@知乎--方差和偏差
@bigdataage --交叉验证(Cross-Validation)
@一只鸟的天空--机器学习中防止过拟合的处理方法
总结:Bias(偏差),Error(误差),Variance(方差)及CV(交叉验证)
标签:方差 攻击 lan 防止 分类器 nal src cross 集中
原文地址:http://www.cnblogs.com/JZ-Ser/p/7476753.html