标签:define size es2017 矩形 复制 com .com col 分析
n * m 的矩形, 有坏点, 问哈密顿回路数量.
n, m <= 11 .
我们考虑轮廓线DP.
为此, 我们要刻画并量化轮廓线的相关信息:
① 插头是否存在?
② 插头的连通性.
我们发现: 插头一一对应, 且互不相交. 于是考虑使用括号序列刻画轮廓线.
至于量化, 我们将一个括号序列当做一个三进制数即可.
从上一行的最后一个, 转移到当前行的第一个: 位移.
当前格子为坏点: 对于没有插头插到当前点的状态原样复制.
否则:
(1) L = # , R = #
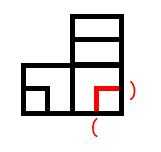
(2) L = ( , U = (
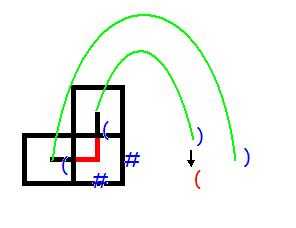
(3) L = ) , U = )
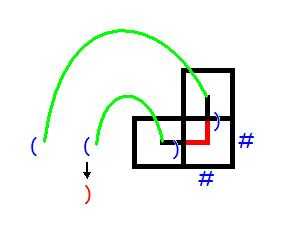
(4) L = ) , U = (
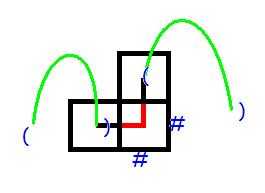
(5) L = ), U = (
只能出现在棋盘的最后一格.
(6) (L != #) ^ (U != #)
两种转移方式均可.
1 #include <cstdio> 2 #include <cstring> 3 #include <cstdlib> 4 #include <cctype> 5 #define F(i, a, b) for (register int i = (a); i <= (b); i++) 6 #define LL long long 7 8 const int N = 15; 9 const int B = 1600000; 10 const int Z = 50000; 11 12 int n, m, Lx, Ly; char s[N][N]; 13 14 #define pos(x) (Dec[s] / Pow[x-1] % 3) 15 int Pow[N], Enc[B], Dec[Z], tot; 16 inline bool Legal(int s) { 17 int cnt = 0; 18 F(i, 0, m) { 19 int key = s / Pow[i] % 3; 20 if (key == 1) cnt++; 21 else if (key == 2) { if (!cnt--) return false; } 22 } 23 return !cnt; 24 } 25 void Hash(void) { 26 Pow[0] = 1; F(i, 1, m+1) Pow[i] = Pow[i-1] * 3; 27 F(s, 0, Pow[m+1]-1) 28 if (Legal(s)) Enc[s] = ++tot, Dec[tot] = s; 29 } 30 31 LL f[Z], g[Z]; 32 33 int main(void) { 34 #ifndef ONLINE_JUDGE 35 freopen("ural1519.in", "r", stdin); 36 #endif 37 38 scanf("%d %d", &n, &m); F(i, 1, n) scanf("%s", s[i]+1); 39 F(i, 1, n) F(j, 1, m) if (s[i][j] == ‘.‘) Lx = i, Ly = j; 40 41 Hash(); 42 43 F(i, 1, n) { 44 if (i == 1) f[Enc[0]] = 1; 45 else { 46 memset(g, 0, sizeof g); 47 F(s, 1, tot) 48 if (Dec[s] < Pow[m]) 49 g[Enc[Dec[s] * 3]] = f[s]; 50 g[0] = 0, memcpy(f, g, sizeof g); 51 } 52 53 F(j, 1, m) { 54 memset(g, 0, sizeof g); 55 if (s[i][j] == ‘*‘) { 56 F(s, 1, tot) 57 g[s] = !pos(j) && !pos(j+1) ? f[s] : 0; 58 } 59 else { 60 F(s, 1, tot) if (f[s] != 0) { 61 int S1 = pos(j), S2 = pos(j+1); 62 if (!S1 && !S2) 63 g[Enc[Dec[s] + Pow[j-1] + 2 * Pow[j]]] += f[s]; 64 else if (!S1 ^ !S2) { 65 g[s] += f[s]; 66 g[Enc[Dec[s] + (S2 - S1) * Pow[j-1] + (S1 - S2) * Pow[j]]] += f[s]; 67 } 68 else if (S1 == 1 && S2 == 2) { 69 if (Lx == i && Ly == j) 70 g[Enc[Dec[s] - Pow[j-1] - 2 * Pow[j]]] += f[s]; 71 } 72 else if (S1 == 2 && S2 == 1) 73 g[Enc[Dec[s] - 2 * Pow[j-1] - Pow[j]]] += f[s]; 74 else if (S1 == 1 && S2 == 1) { 75 int cnt = 1, id = j+1; 76 for (id++; ; id++) 77 if (pos(id) == 1) cnt++; 78 else if (pos(id) == 2) { if (!--cnt) break; } 79 g[Enc[Dec[s] - Pow[j-1] - Pow[j] - Pow[id-1]]] += f[s]; 80 } 81 else { 82 int cnt = -1, id = j; 83 for (id--; ; id--) 84 if (pos(id) == 2) cnt--; 85 else if (pos(id) == 1) { if (!++cnt) break; } 86 g[Enc[Dec[s] - 2 * Pow[j-1] - 2 * Pow[j] + Pow[id-1]]] += f[s]; 87 } 88 } 89 } 90 g[0] = 0, memcpy(f, g, sizeof g); 91 } 92 } 93 printf("%lld\n", f[Enc[0]]); 94 95 return 0; 96 }
[URAL 1519] Formula 1 轮廓线DP 括号序列
标签:define size es2017 矩形 复制 com .com col 分析
原文地址:http://www.cnblogs.com/Sdchr/p/7478253.html