标签：目标 写作 回归 斯坦福 无限 价值 统计学 class 学习方法
http://mp.weixin.qq.com/s?__biz=MzIxNDIwMTk2OQ==&mid=2649077019&idx=1&sn=e0c4a6c502e3668e1dc410f21e531cfd&scene=0#wechat_redirect
https://wizardforcel.gitbooks.io/dm-algo-top10/content/svm-4.html、
首先，核函数是什么？到底什么是核函数？
个人理解为：核函数！=内积！=映射！=相似度，核函数是一种表征映射、实现内积逻辑关系且降低计算复杂度的一类特殊函数(满足Mercer‘s condition)！
下面给出官方核函数的定义，其定义如下(可参考统计学习方法)：
设X是输入空间（欧氏空间或离散集合），Η为特征空间（希尔伯特空间），如果存在一个从X到Η的映射
φ(x): X→Η
使得对所有的x,y∈X,函数Κ(x,y)=φ(x)?φ(y)，
则称Κ(x,y)为核函数，φ(x)为映射函数，φ(x)?φ(y)为x,y映射到特征空间上的内积。
在该定义中，涉及到几个概念：输入空间、特征空间、以及Mercer‘s condition。那先从空间说起。简单来说，常见的空间有欧式空间，集合(离散)，赋范空间，希尔伯特空间。常见的欧式空间，即平常我们见到1,2……n维且满足可度量条件的空间(注：也可查看欧式五大公理)。而赋范空间通俗的理解就是距离+线性结构+范数=赋范空间，而在赋范空间+内积运算+完备性=希尔伯特空间。关于空间定义中几个概念下面给出简单解释：
距离的定义：设任意非空集合X，对X中任意两点x,y,满足一个实数d(x,y):
d(x,y)<=0,当且仅当d(x,y)=0或者x=y;d(x,y)=d(y,x),d(x,y)<=d(x,z)+d(z,y)[类勾股定理]
线性结构：指的是加减乘除，交换律，结合律等
范数：空间点到空间零点的距离
内积运算：引入空间中角的概念
完备性： 内包含任意极限(通俗理解即永远逃不出的空间体系)
接下来看一下Mercer‘s condition，Mercer定理是指，函数需满足对称性和正定性，所谓的对称性就是比如上述定义中φ(x)?φ(y)= φ(y)?φ(x),而所谓的正定性定义如下(核函数会对应Gram矩阵)，当矩阵M所有的特征值大于零的前提下，根据谱定理，必然存在一个对角矩阵D与M相似(M = P-1DP),通俗的理解就是点M落在以P-1，P 为基的空间中，其特征值M就是在这组基空间下的具体点值。
矩阵正定性有很多好处，如：可逆，迹大于0，运算正定…….而至于为什么梅歇尔定理要求正定呢？自己也还不是很清楚，个人理解就是正定性使得函数极限方向唯一且大于等于零，同时正定性产生的优化问题都是有良好凸优化性质(凸函数收敛到局部最优值即为全局最优值，是不是立马想到了梯度下降法)，从而把原始空间的度量概念能移植到特征空间(融入了角和内积)中去(可拍砖)。
其次，数据在什么情况下可以用核函数？
从个人理解出发，即只要在原始数据维度大于零且涉及空间度量的前提下，都可以运用核函数方法(诚然，最后是否选择还需要根据优化目标进行决定)。也正是基于此，很多在使用核函数方法时就会陷入一个误区，简单认为核函数就是一个从低纬度映射到高维度的函数，核函数在特征变换时，的确会包含了映射这一层个逻辑，但是低纬度到高纬度的表述就不严谨了，因为常规的空间是有度量的，即有维度的概念，但是希尔伯特空间已经延展至无限维度（即没有维度的定义了），故再谈维度，已然没有任何意义了！
接下来，在这里说一下正常思维的理解下的核函数：
1、找到映射函数（映射到高维空间去）
2、高维空间里面通过内积（其实内积仅仅是其中一种在高维空间里面度量其数据相似度一种手段，这里的相似度可能定义不准确，可以这么说，算是常规空间中度量的一种标准）
3、优化问题求解
4、最优解还原到原始空间
这种思路是正常的，也是合理的。但是从核函数产生的过程来看，这种思路恰好和核函数本质逻辑是逆向的，其实这里引用网友一个通俗的比喻：
故事应该是这样的，那些做支持向量机、特征变换的人，发现自己的算法对数据集的效果不好，他们认为这可能是因为数据集线性不可分(假设，实际可能不是这样)。另外他们发现他们搞出的式子里，出现的都是两个数据点的内积。他们认为要是把原始数据集映射到高维可能就线性可分(增加可分的概率)，但是这可是内积，而且怎么找映射函数呢？这时候Mercer Theorem出现了，那就构造一个kernel function。根据Mercer Theorem，那些原始维度的内积转换到高维内积只需要把数据点带进核函数就可以了。
是不是很简单？结果在数据集上反应居然出奇的好，之后这种方法便出现了很多时髦名称。
所以透过这个故事，可以看到，实际当中核函数只是在表达的时候，可以说内包含了映射，内积,相似度这些逻辑，但这个映射，内积以及相似度的具体表达式以及过程不需要也没有必要显示表征出来，最终直接通过核函数在低维空间中实现映射到高维空间之后的最终内积结果。
最后的4点总结：
1、核函数是一种满足条件梅歇尔条件的函数，包含映射，内积，相似度的逻辑，但具体的这些逻辑不要显示表征出来
2、核函数深层次原理就是通过变换特征空间并在特征空间中组合有限的平滑函数对求解问题进行优化(所有的平滑函数都能通过麦克劳林展开式近似计算，从而为映射到无穷维度提供可能)
3、核函数映射到维空间，仅仅是增加了数据可分性，并不是代表一定可分，借用一句网友较形象的比如：We are safe but not certain！
4、有很多人问，怎么去选择核函数（线性核、多项式核、sigmoid核……），那针对特定问题如何选择一个较好的核函数去学习能获得较好的模型能力呢？还有就是，在希尔伯特空间映射下，数据到底变换为多少维度？有穷还是无穷？，这对这些问题，我会在接下来继续把自己的一些看法继续以纪要的形式发出来，也希望广大网友能多多批评和指正！
一、核函数的引入
问题1：
SVM显然是线性分类器，但数据如果根本就线性不可分怎么办？
解决方案1：
数据在原始空间（称为输入空间）线性不可分，但是映射到高维空间（称为特征空间）后很可能就线性可分了。
问题2：
映射到高维空间同时带来一个问题：在高维空间上求解一个带约束的优化问题显然比在低维空间上计算量要大得多，这就是所谓的“维数灾难”。
解决方案2：
于是就引入了“核函数”，核函数的价值在于它虽然也是讲特征进行从低维到高维的转换。
二、实例说明 例如图中的两类数据，分别分布为两个圆圈的形状，不论是任何高级的分类器，只要它是线性的，就没法处理，SVM 也不行。因为这样的数据本身就是线性不可分的。
从上图我们可以看出一个理想的分界应该是一个“圆圈”而不是一条线（超平面）。如果用 X1 和 X2 来表示这个二维平面的两个坐标的话，我们知道一条二次曲线（圆圈是二次曲线的一种特殊情况）的方程可以写作这样的形式：
a1X1+a2X21+a3X2+a4X22+a5X1X2+a6=0
注意上面的形式，如果我们构造另外一个五维的空间，其中五个坐标的值分别为 Z1=X1, Z2=X21, Z3=X2, Z4=X22, Z5=X1X2，那么显然，上面的方程在新的坐标系下可以写作：
∑i=15aiZi+a6=0
关于新的坐标 Z ，这正是一个超平面 的方程！也就是说，如果我们做一个映射 ?:R2→R5 ，将 X 按照上面的规则映射为 Z ，那么在新的空间中原来的数据将变成线性可分的，从而使用之前我们推导的线性分类算法就可以进行处理了。这正是 Kernel 方法处理非线性问题的基本思想。
三、详细分析
还记得之前我们用内积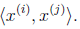
这里是二维模型，但是现在我们需要三维或者更高的维度来表示样本。这里我们假设是维度是三；
那么首先需要将特征x扩展到三维
，然后寻找特征和结果之间的模型。我们将这种特征变换称作特征映射（feature mapping）。映射函数称作
，在这个例子中
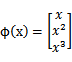
我们希望将得到的特征映射后的特征应用于SVM分类，而不是最初的特征。这样，我们需要将前面
公式中的内积从
，映射到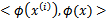
。
为什么需要映射后的特征而不是最初的特征来参与计算，一个重要原因是样例可能存在线性不可分的情况，而将特征映射到高维空间后，往往就可分了。
核函数的定义：
将核函数形式化定义，如果原始特征内积是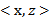
，映射后为
，那么定义核函数（Kernel）为
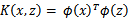
现在有了以上的概念，我们现在要计算K(x,z)只要简单的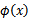计算
，然后计算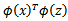
，在求出它们的内积。但是现在有一个问题，那是计算K(x,z)的时间复杂度是提高了。即使是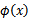计算也是很复杂的。那现在怎么解决呢？
现在我们假设：x，z都是n维，同时有
展开
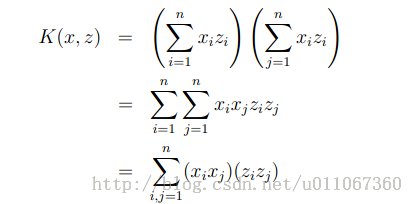
发现我们可以只计算原始特征x和z内积的平方（时间复杂度是O(n)），就等价与计算映射后特征的内积。也就是说我们不需要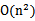
时间了。
现在看一下映射函数（n=3时），根据上面的公式，得到
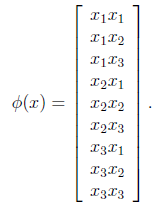
也就是说核函数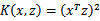
只能在选择这样的
作为映射函数时才能够等价于映射后特征的内积。
再看一个核函数
对应的映射函数（n=3时）是
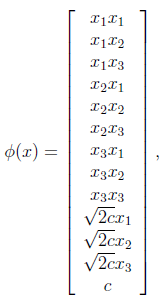
更一般地，核函数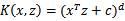
对应的映射后特征维度为
。
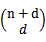四、如何映射到核函数
现在介绍了核函数之后那到底怎么来使用核函数到样本了？
设超平面实际的方程是这个样子（圆心在 X2 轴上的一个正圆）：
a1X21+a2(X2?c)2+a3=0
因此我只需要把它映射到 Z1=X21, Z2=X22, Z3=X2 这样一个三维空间中即可，下图是映射之后的结果，将坐标轴经过适当的旋转，就可以很明显地看出，数据是可以通过一个平面来分开的：
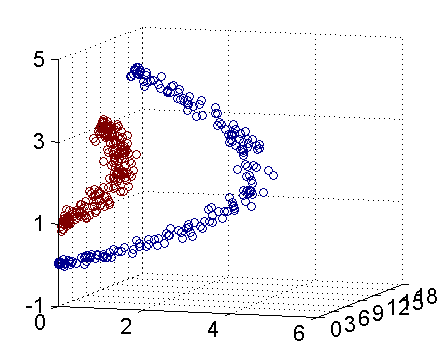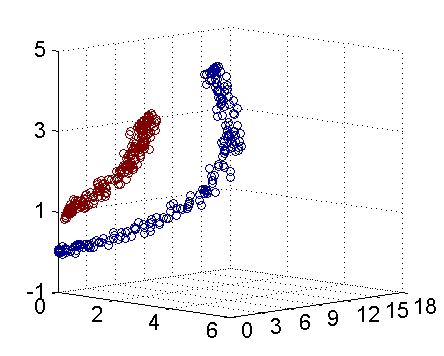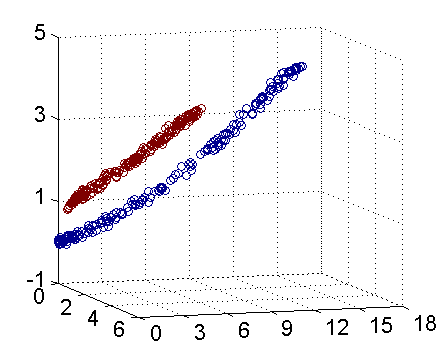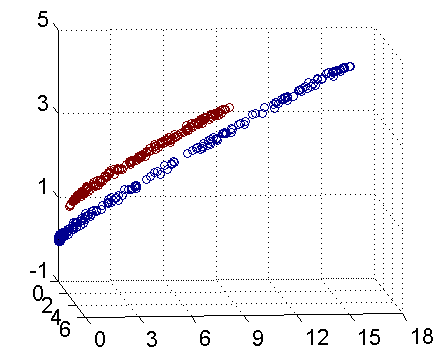
现在让我们再回到 SVM 的情形，假设原始的数据时非线性的，我们通过一个映射 ?(?) 将其映射到一个高维空间中，数据变得线性可分了，这个时候，我们就可以使用原来的推导来进行计算，只是所有的推导现在是在新的空间，而不是原始空间中进行。
我们上一次得到的最终的分类函数是这样的：
现在则是在映射过后的空间，即：
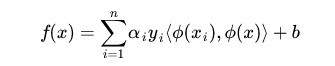
而其中的 α 也是通过求解如下 dual 问题而得到的：
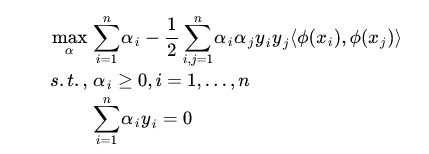
回到我们之前构造的一个五维的空间：到现在貌似我们还没有用到核函数，但是现在我们可以看出，数据映射到新空间后，因为新空间是多维的，计算量肯定是增加了不少了，现在就只能用核函数来解决了。
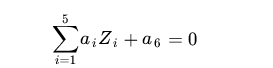
不妨还是从最开始的简单例子出发，设两个向量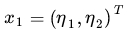
和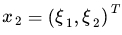 
，而?(*) 即是到前面说的五维空间的映射，
五个坐标的值分别为 Z1=X1, Z2=X21, Z3=X2, Z4=X22, Z5=X1X2，
因此映射过后的内积为：
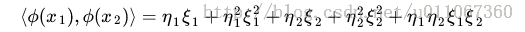
根据我们之前简介的核函数的实现，具体来说，上面这个式子的计算结果实际上映射了
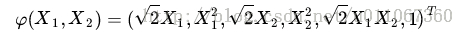
这样一来计算的问题就算解决了，避开了直接在高维空间中进行计算，而结果却是等价的。
五、高斯核函数
再看另外一个核函数
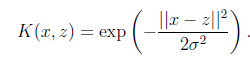
这时，如果x和z很相近（
），那么核函数值为1，如果x和z相差很大（
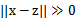），那么核函数值约等于0。由于这个函数类似于高斯分布，因此称为高斯核函数，也叫做径向基函数(Radial Basis Function 简称RBF)。它能够把原始特征映射到无穷维。
既然高斯核函数能够比较x和z的相似度，并映射到0到1，回想logistic回归，sigmoid函数可以，因此还有sigmoid核函数等等。
注意，使用核函数后，怎么分类新来的样本呢？线性的时候我们使用SVM学习出w和b，新来样本x的话，我们使用
来判断，如果值大于等于1，那么是正类，小于等于是负类。在两者之间，认为无法确定。如果使用了核函数后，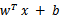
就变成了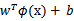
，是否先要找到
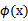，然后再预测？答案肯定不是了，找
很麻烦，回想我们之前说过的
只需将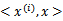
替换成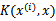
，然后值的判断同上。
总结：对于非线性的情况，SVM 的处理方法是选择一个核函数 κ(*) ，通过将数据映射到高维空间，来解决在原始空间中线性不可分的问题。由于核函数的优良品质，这样的非线性扩展在计算量上并没有比原来复杂多少，这一点是非常难得的。当然，这要归功于核方法——除了 SVM 之外，任何将计算表示为数据点的内积的方法，都可以使用核方法进行非线性扩展。
参考文档：（ 主要的参考文档来自4个地方）
4、斯坦福大学机器学习的公开课。
https://royalsociety.org/science-events-and-lectures/2014/11/milner-lecture/
标签：目标 写作 回归 斯坦福 无限 价值 统计学 class 学习方法
原文地址：http://www.cnblogs.com/JZ-Ser/p/7479757.html
