标签:style const src dfs noi inf ios 格式 不能
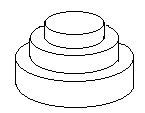
7月17日是Mr.W的生日,ACM-THU为此要制作一个体积为Nπ的M层
生日蛋糕,每层都是一个圆柱体。
设从下往上数第i(1<=i<=M)层蛋糕是半径为Ri, 高度为Hi的圆柱。当i<M时,要求Ri>Ri+1且Hi>Hi+1。
由于要在蛋糕上抹奶油,为尽可能节约经费,我们希望蛋糕外表面(最下一层的下底面除外)的面积Q最小。
令Q= Sπ
请编程对给出的N和M,找出蛋糕的制作方案(适当的Ri和Hi的值),使S最小。
(除Q外,以上所有数据皆为正整数)
输入格式:
有两行,第一行为N(N<=20000),表示待制作的蛋糕的体积为Nπ;第二行为M(M<=15),表示蛋糕的层数为M。
输出格式:
仅一行,是一个正整数S(若无解则S=0)。
100 2
68
分析:裸搜只有10分。。。。。。其实这就是一道搜索的题,关键是要怎么剪枝。可以很容易想出两个剪枝:
1.当前体积+以后的最小体积>n,剪枝.
2.当前表面积+以后的最小表面积>ans,剪枝.
第一个是很好处理的,关键是第二个剪枝,如果直接用最小的i和h来算,在体积上不能保证满足要求,有一个定理是如果体积一定,半径越大,表面积越小,因为在体积中半径的增长是平方级的,这样我们接下来每一层和这一层的半径相同,那么就是最小表面积了(虽然永远也达不到,但是不会把正解给剪掉),保证体积满足要求,我们只需要用剩下的体积除以当前层的半径就好了.
#include <cstdio> #include <cstring> #include <iostream> #include <cmath> #include <algorithm> using namespace std; const int inf = 0x7ffffff; int n,m,ans = inf,qs[50],qv[50]; void dfs(int cnt,int s,int v,int r,int h) { if (cnt == 0) { if (v == n) ans = min(ans,s); return; } //剪枝 if (v + qv[cnt] > n) return; if (s + (n - v) / r > ans) return; for (int i = r - 1; i >= cnt; i--) { if (cnt == m) s = i * i; for (int j = h - 1; j >= cnt; j--) dfs(cnt - 1,2 * i * j + s,v + i * i * j,i,j); } } int main() { scanf("%d%d",&n,&m); for (int i = 1; i <= m; i++) { int t2 = i * i * i; qv[i] += qv[i-1] + t2; } dfs(m,0,0,sqrt(n),n); if (ans != inf) printf("%d\n",ans); else printf("0\n"); return 0; }
标签:style const src dfs noi inf ios 格式 不能
原文地址:http://www.cnblogs.com/zbtrs/p/7479851.html