标签:hint int 处理 res 双向 数学 bzoj cstring uil
Description
世界树是一棵无比巨大的树,它伸出的枝干构成了整个世界。在这里,生存着各种各样的种族和生灵,他们共同信奉着绝对公正公平的女神艾莉森,在他们的信条里,公平是使世界树能够生生不息、持续运转的根本基石。
世界树的形态可以用一个数学模型来描述:世界树中有n个种族,种族的编号分别从1到n,分别生活在编号为1到n的聚居地上,种族的编号与其聚居地的编号相同。有的聚居地之间有双向的道路相连,道路的长度为1。保证连接的方式会形成一棵树结构,即所有的聚居地之间可以互相到达,并且不会出现环。定义两个聚居地之间的距离为连接他们的道路的长度;例如,若聚居地a和b之间有道路,b和c之间有道路,因为每条道路长度为1而且又不可能出现环,所卧a与c之间的距离为2。
出于对公平的考虑,第i年,世界树的国王需要授权m[i]个种族的聚居地为临时议事处。对于某个种族x(x为种族的编号),如果距离该种族最近的临时议事处为y(y为议事处所在聚居地的编号),则种族x将接受y议事处的管辖(如果有多个临时议事处到该聚居地的距离一样,则y为其中编号最小的临时议事处)。
现在国王想知道,在q年的时间里,每一年完成授权后,当年每个临时议事处将会管理多少个种族(议事处所在的聚居地也将接受该议事处管理)。 现在这个任务交给了以智慧著称的灵长类的你:程序猿。请帮国王完成这个任务吧。
Input
第一行为一个正整数n,表示世界树中种族的个数。
接下来n-l行,每行两个正整数x,y,表示x聚居地与y聚居地之间有一条长度为1的双
向道路。接下来一行为一个正整数q,表示国王询问的年数。
接下来q块,每块两行:
第i块的第一行为1个正整数m[i],表示第i年授权的临时议事处的个数。
第i块的第二行为m[i]个正整数h[l]、h[2]、…、h[m[i]],表示被授权为临时议事处的聚居地编号(保证互不相同)。
Output
输出包含q行,第i行为m[i]个整数,该行的第j(j=1,2…,,m[i])个数表示第i年被授权的聚居地h[j]的临时议事处管理的种族个数。
Sample Input
10
2 1
3 2
4 3
5 4
6 1
7 3
8 3
9 4
10 1
5
2
6 1
5
2 7 3 6 9
1
8
4
8 7 10 3
5
2 9 3 5 8
Sample Output
1 9
3 1 4 1 1
10
1 1 3 5
4 1 3 1 1
HINT
N<=300000, q<=300000,m[1]+m[2]+…+m[q]<=300000
Sourc
好久没有打这么刺激的题了。。。
题目中明确告诉你每个询问有k个关键点,且∑k为线性,看起来就很虚树。。。
首先把虚树构建出来,在虚树上通过两边dp,求出虚树上所有点的归属点。。。
(第一遍用儿子更新父亲,第二遍用父亲更新儿子,树型dp正常套路。。。)
然后考虑尚未在虚树中出现的点,这个的话感觉讲不太清楚,画一下图吧。。。
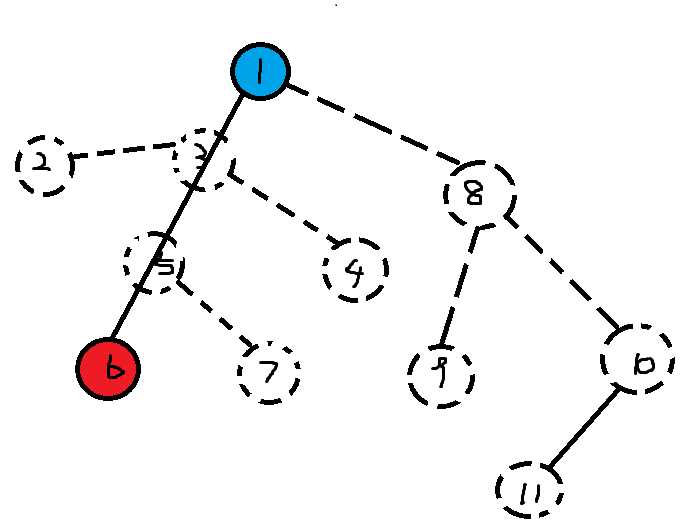
假设1,6是虚树上的点,且1属于蓝色,6属于红色,然后虚线的点表示还不在虚树上的点,他们有一下几种情况。。。
1.夹在了虚树的一条边上(a,b)(如2,3,4,5,7号节点)
假如a和b的归属点相同,那么2,3,4,5,7号节点的归属点应该和a,b的颜色相同;
假如a和b的颜色不同,那么路径上必然存在一个分界点,使得一边归a管,一边归b管,那么这个可以通过倍增来找到分界点。。。
2.没有夹在虚树的一条边上(如8,9,10,11号节点)那么这些节点的归属点必然就是这一片子树的父亲的归属点。。。
这样看来嘴巴AC还是比较容易的,具体有一些实现的细节。。。
对于一条边(a,b)(假设deep[a]<deep[b]),需要找到一个既是a的儿子又是b的祖先的一个点x,也就是a的儿子中子树里含b的点,也就是只考虑夹在路径间的。。。
那么如果a,b同色,那么ans[bel[a]]+=size[x];
如果a,b不同色,我们通过倍增找到了路径上的分界点mid,然后ans[bel[a]]+=size[x]-size[mid],ans[bel[b]]+=size[mid]-size[b];
然后考虑第二种情况,我们用res数组,res[i]表示i的子树中还没有归属点的点数(初始值为size[i]),那么res数组在处理第一种情况的时候,即时res[i]-size[x]即可,最后再加上;
// MADE BY QT666
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<iostream>
#include<cstring>
using namespace std;
typedef long long ll;
const int N=1000050;
struct data{
int head[N],to[N],nxt[N],v[N],cnt;
void lnk(int x,int y){
if(x==y) return;
to[++cnt]=y,nxt[cnt]=head[x],head[x]=cnt;
to[++cnt]=x,nxt[cnt]=head[y],head[y]=cnt;
}
}g,g2;
int size[N],dfn[N],tt,son[N],top[N],fa[N],deep[N],n,q,k;
int a[N],b[N],zhan[N],bel[N],Father[N][20],ans[N],res[N],tot,xu[N];
bool cmp(int a,int b){return dfn[a]<dfn[b];}
void dfs1(int x,int f){
size[x]=1;fa[x]=f;Father[x][0]=f;
for(int i=1;i<=17;i++) Father[x][i]=Father[Father[x][i-1]][i-1];
for(int i=g.head[x];i;i=g.nxt[i]){
int y=g.to[i];if(y==f) continue;
deep[y]=deep[x]+1;dfs1(y,x);
size[x]+=size[y];if(size[y]>size[son[x]]) son[x]=y;
}
}
void dfs2(int x,int f){
top[x]=f;dfn[x]=++tt;
if(son[x]) dfs2(son[x],f);
for(int i=g.head[x];i;i=g.nxt[i]){
int y=g.to[i];if(y==fa[x]||y==son[x]) continue;
dfs2(y,y);
}
}
int Lca(int x,int y){
while(top[x]!=top[y]){
if(deep[top[x]]<deep[top[y]]) swap(x,y);
x=fa[top[x]];
}
if(deep[x]<deep[y]) swap(x,y);
return y;
}
int calc(int x,int y){return deep[x]+deep[y]-2*deep[Lca(x,y)];}
void DFS1(int x,int f){
res[x]=size[x];xu[++tot]=x;
for(int i=g2.head[x];i;i=g2.nxt[i]){
int y=g2.to[i];if(y==f) continue;
DFS1(y,x);
if(bel[y]){
if(!bel[x]) bel[x]=bel[y];
else{
int d1=calc(x,bel[x]),d2=calc(x,bel[y]);
if(d2<d1||(d2==d1&&bel[y]<bel[x])) bel[x]=bel[y];
}
}
}
}
void DFS2(int x,int f){
for(int i=g2.head[x];i;i=g2.nxt[i]){
int y=g2.to[i];if(y==f) continue;
if(bel[x]){
if(!bel[y]) bel[y]=bel[x];
else{
int d1=calc(y,bel[y]),d2=calc(y,bel[x]);
if(d2<d1||(d2==d1&&bel[x]<bel[y])) bel[y]=bel[x];
}
}
DFS2(y,x);
}
}
void build(){
scanf("%d",&k);tot=0;
for(int i=1;i<=k;i++) scanf("%d",&a[i]),bel[a[i]]=a[i],b[i]=a[i];
sort(a+1,a+1+k,cmp);int tp=0;g2.cnt=1;if(!bel[1]) zhan[++tp]=1;
for(int i=1;i<=k;i++){
if(tp==0){zhan[++tp]=a[i];continue;}
int p=Lca(zhan[tp],a[i]);
while(1){
if(deep[zhan[tp-1]]<=deep[p]){
g2.lnk(zhan[tp],p);tp--;
if(zhan[tp]!=p) zhan[++tp]=p;
break;
}
g2.lnk(zhan[tp],zhan[tp-1]);tp--;
}
zhan[++tp]=a[i];
}
while(tp>1) g2.lnk(zhan[tp],zhan[tp-1]),tp--;
DFS1(zhan[tp],zhan[tp]);DFS2(zhan[tp],zhan[tp]);
}
void solve(int x,int y){
int g=y;if(deep[x]>deep[y]) swap(x,y);
for(int i=17;i>=0;i--){
if(Father[g][i]&&deep[Father[g][i]]>deep[x]) g=Father[g][i];
}
res[x]-=size[g];
if(bel[x]==bel[y]){ans[bel[x]]+=size[g]-size[y];return;}
int mid=y;
for(int i=17;i>=0;i--){
int Mid=Father[mid][i];
int d1=calc(bel[x],Mid),d2=calc(bel[y],Mid);
if(!Mid) continue;
if((d2<d1||(d2==d1&&bel[y]<bel[x]))&&deep[Mid]>=deep[g]) mid=Mid;
}
ans[bel[x]]+=size[g]-size[mid];ans[bel[y]]+=size[mid]-size[y];
}
int main(){
scanf("%d",&n);
for(int i=1;i<n;i++){int x,y;scanf("%d%d",&x,&y);g.lnk(x,y);}
dfs1(1,0);dfs2(1,1);scanf("%d",&q);
while(q--){
build();
for(int i=2;i<=g2.cnt;i+=2) solve(g2.to[i],g2.to[i^1]);
for(int i=1;i<=tot;i++) ans[bel[xu[i]]]+=res[xu[i]];
for(int i=1;i<=k;i++) printf("%d ",ans[b[i]]),ans[b[i]]=0;
puts("");for(int i=1;i<=tot;i++) g2.head[xu[i]]=0,bel[xu[i]]=0;
}
return 0;
}
bzoj 3572: [Hnoi2014]世界树
标签:hint int 处理 res 双向 数学 bzoj cstring uil
原文地址:http://www.cnblogs.com/qt666/p/7481769.html

