标签:保留 合成 math 审批 输出 include iostream 结束 i++
某国有n个城市,它们互相之间没有公路相通,因此交通十分不便。为解决这一“行路难”的问题,政府决定修建公路。修建公路的任务由各城市共同完成。
修建工程分若干轮完成。在每一轮中,每个城市选择一个与它最近的城市,申请修建通往该城市的公路。政府负责审批这些申请以决定是否同意修建。
政府审批的规则如下:
(1)如果两个或以上城市申请修建同一条公路,则让它们共同修建;
(2)如果三个或以上的城市申请修建的公路成环。如下图,A申请修建公路AB,B申请修建公路BC,C申请修建公路CA。则政府将否决其中最短的一条公路的修建申请;

(3)其他情况的申请一律同意。
一轮修建结束后,可能会有若干城市可以通过公路直接或间接相连。这些可以互相:连通的城市即组成“城市联盟”。在下一轮修建中,每个“城市联盟”将被看作一个城市,发挥一个城市的作用。
当所有城市被组合成一个“城市联盟”时,修建工程也就完成了。
你的任务是根据城市的分布和前面讲到的规则,计算出将要修建的公路总长度。
输入格式:
第一行一个整数n,表示城市的数量。(n≤5000)
以下n行,每行两个整数x和y,表示一个城市的坐标。(-1000000≤x,y≤1000000)
输出格式:
一个实数,四舍五入保留两位小数,表示公路总长。(保证有惟一解)
4 0 0 1 2 -1 2 0 4
6.47
修建的公路如图所示: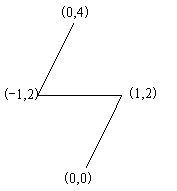
prim求最小生成树
#include<cmath> #include<cstdio> #include<cstring> #include<cstdlib> #include<iostream> #include<algorithm> #define N 5100 #define maxn 9999999 using namespace std; double s[N],l[N]; int n,m,fa[N*N]; long long x,y,t,sum,fx,fy,xx[N*N],yy[N*N]; int read() { int x=0,f=1; char ch=getchar(); while(ch<‘0‘||ch>‘9‘){if(ch==‘-‘)f=-1; ch=getchar();} while(ch>=‘0‘&&ch<=‘9‘){x=x*10+ch-‘0‘; ch=getchar();} return x*f; } struct Edge { int x,y; double z; }edge[N<<1]; int cmp(Edge a,Edge b) { return a.z<b.z; } int find(int x) { if(fa[x]==x) return x; fa[x]=find(fa[x]); return fa[x]; } int prim(int x) { double ans=0; for(int i=1;i<=n;i++) { s[i]=x; l[i]=sqrt((xx[x]-xx[i])*(xx[x]-xx[i])+(yy[x]-yy[i])*(yy[x]-yy[i])); } s[x]=-1; for(int i=1;i<=n;i++) { t=-1;sum=maxn; for(int j=1;j<=n;j++) if(s[j]!=-1&&sum>l[j]) { sum=l[j]; t=j; } if(t!=-1) { s[t]=-1;ans+=l[t]; for(int j=1;j<=n;j++) { double ss=sqrt((xx[t]-xx[j])*(xx[t]-xx[j])+(yy[t]-yy[j])*(yy[t]-yy[j])); if(s[j]!=-1&&ss<l[j]) { l[j]=ss; s[j]=t; } } } } printf("%.2lf",ans); } int main() { n=read(); for(int i=1;i<=n;i++) xx[i]=read(),yy[i]=read(); prim(1); return 0; }
标签:保留 合成 math 审批 输出 include iostream 结束 i++
原文地址:http://www.cnblogs.com/z360/p/7481808.html