标签:_id 判断 输入输出格式 求和 include mat style bit ensure
你以为真的是模板?

输入格式:

输出格式:

2 10 4 6
5
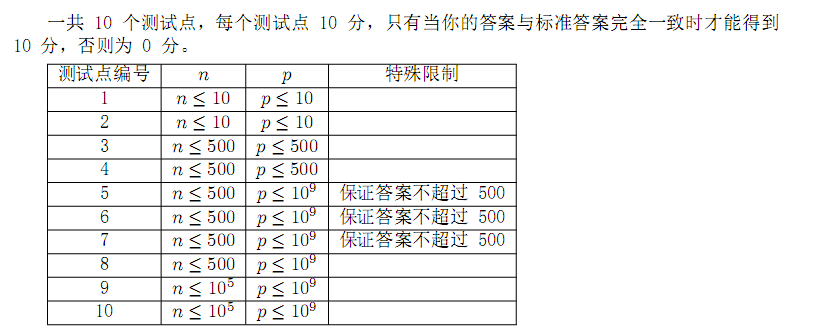
题目大意 :一开始给A集合,即为n个数。 为B集合的子集,然后从A集合中任意取出两个数(可以取重复的一个数)相加%p一定的B集合中
求b集合的大小最小是多少
题解:B集合最大为p知道吧;;;
求出N个数的最大公约数gg,在不考虑模p的情况下,随便两个数相加得到的数一定是gg的倍数,
所以0--p-1为gg倍数的一定存在B集合,可怕的是如果相加的数%p,不是gg的倍数,最大公约数改变了,
那么B集合中出现的数就不止gg的倍数了。具体看代码 玄学AC。考试是,我只判断了如果n个数的gcd为1
B的大小就为p水30分。
代码
#include<iostream> #include<cstdio> using namespace std; int n,p,tmp,x; int gcd(int x,int y){ return y==0?x:gcd(y,x%y); } int main(){ scanf("%d%d",&n,&p);tmp=p; for(int i=1;i<=n;i++){ scanf("%d",&x); tmp=gcd(tmp,x); } printf("%d\n",p/tmp); return 0; }
有一个长度为nn的序列AA,每个数A_i (1 \leq i \leq n )A?i??(1≤i≤n)都满足1 \leq A_i \leq n1≤A?i??≤n
我们定义这个序列的恶心程度为j-i+1j?i+1的最大值,其中A_iA?i??,A_{i+1}A?i+1??,···,A_jA?j?? 都相等。
现在你最多能操作TT次,每次操作都是把相邻的两个数交换。问该序列的恶心程度最大能到多少。
输入格式:
第一行两个整数nn,TT
第二行有nn个整数,第ii个数表示A_iA?i??
输出格式:
一个整数,表示该序列最大的恶心程度
7 3 3 2 2 4 3 2 3
3
【样例解释】
一种最优方案是,先将最右边的一个22与它左边的33交换,再将这个22与它左边的44交换,这样恶心程度是33
【数据范围】
对于所有测试点,1 \leq T \leq n^21≤T≤n?2??
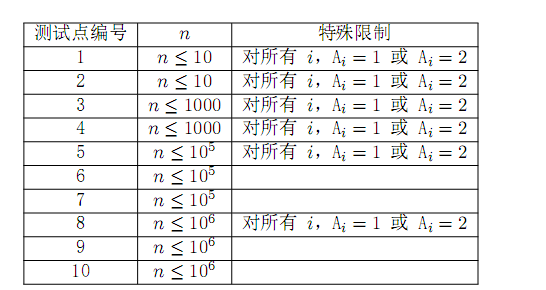
题目大意: 给出一个序列,n个数。这个序列的开心值(题目扯谈=u=)为最长的连续相等的子序列的长度,
一共给出t此操作,每次操作可以交换相邻的两个数 求最大的开心值。
题解:看数据范围应该是个二分...然而我不会写judge函数...,然后正解是二分,找出每一个数能够在t次操作内形成的最长连续长度。
判断使第i--j个x在一起需要几次操作。
long long cal(int l,int r){ int m=(l+r)>>1; return 1LL*A[m]*(2*m-l-r)+(sum[r]-sum[m])-(sum[m-1]-sum[l-1])-((m-l)*(m-l+1)+(r-m)*(r-m+1))/2; }
解释一下。使第l--r的x在一起的最小操作怎样求。最小肯定是要往中间聚合。
1LL转成long long
A[m]*(2*m-l-r) 其中(2*m-l-r),当m是中间的那个x时(即我们要聚集到的x)(2*m-l-r)为0,否则为-1.(至于为什么-1,待会。)
(sum[r]-sum[m])-(sum[m-1]-sum[l-1]) 是计算中间x的右边的点到左边的点的距离和 (你随便一一对应就好啦),为聚集到中间那个点的距离。注意到是到中间那个点上。
如果第一个的(2*m-l-r)为-1的话 就默认为中间x左边的点,所以聚集时不是算出的中间的点了 而是 ...比如 。 。 。 。,聚集到第二个和第三个中间。
((m-l)*(m-l+1)+(r-m)*(r-m+1))/2。这个是因为我们聚集时是聚集在一个地方形成了个点。所以我们需要左边的点退1格,退两格...从右边来的点同。
为1+2+3+4....等差序列求和公式。
代码
#include<iostream> #include<vector> #include<cstdio> using namespace std; vector<int>pos[1000006]; int *A; int n,x,ans; long long t; int sum[1000006]; long long cal(int l,int r){ int m=(l+r)>>1; return 1LL*A[m]*(2*m-l-r)+(sum[r]-sum[m])-(sum[m-1]-sum[l-1])-((m-l)*(m-l+1)+(r-m)*(r-m+1))/2; } int slove(int n){ int r=1,s=0; for(int i=1;i<=n;i++)sum[i]=sum[i-1]+A[i]; for(int i=1;i<=n;i++){ if(r<i)r=i; while(r<n&&cal(i,r+1)<=t)r++; s=max(s,r-i+1); } return s; } int main(){ scanf("%d%lld",&n,&t); for(int i=1;i<=n;i++){ scanf("%d",&x); pos[x].push_back(i); } for(int i=1;i<=n;i++){ if(!pos[i].empty()){ A=&pos[i].front()-1; ans=max(ans,slove(pos[i].size())); } } printf("%d\n",ans); return 0; }
T3
好吧,这不是模板

输入格式:

输出格式:

a b bb 4 4 1 5 4 1 1 4 2 4 6 2 11
1 0 1 2
【样例解释】
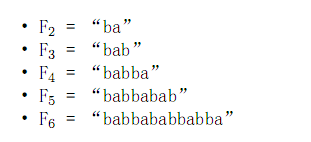
【数据范围】
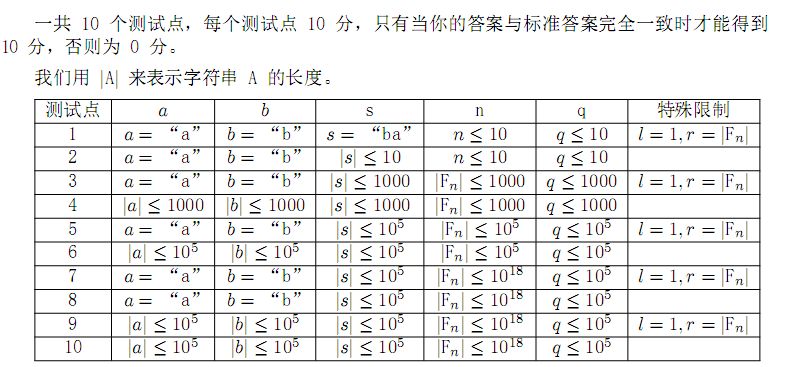
我真不会...贴标程吧...
代码
#include <stdio.h> #include <string.h> #include <string> #include <assert.h> #include <bits/stdc++.h> #define debug(...) //fprintf(stderr, __VA_ARGS__) #define MAXN 100005 #define base 313 #define mo 1000000009 using namespace std; char a[MAXN], b[MAXN], s[MAXN]; int len_s; int h_s; inline void init_hash() { int base_pow = 1; int i; for (i = 0; i < len_s; i++) { h_s = (h_s + 1LL * base_pow * s[i]) % mo; base_pow = 1LL * base_pow * base % mo; } } inline int count(const char *a, int len_a, int *sum) { int base_pow = 1; int i; int h_a = 0; for (i = 0; i < len_s; i++) { h_a = (h_a + 1LL * base_pow * a[i]) % mo; base_pow = 1LL * base_pow * base % mo; } int ret = h_s == h_a; sum[0] = 0; sum[1] = ret; int tmp_h_s = h_s; int base_pow_2 = 1; for (i = len_s; i < len_a; i++) { tmp_h_s = 1LL * tmp_h_s * base % mo; h_a = (h_a + 1LL * base_pow * a[i] - 1LL * base_pow_2 * a[i - len_s]) % mo; h_a = (h_a + mo) % mo; ret += tmp_h_s == h_a; sum[i - len_s + 2] = ret; base_pow = 1LL * base_pow * base % mo; base_pow_2 = 1LL * base_pow_2 * base % mo; } return ret; } inline int count(const std::string &a, int *sum) { return count(a.c_str(), a.length(), sum); } int q; std::string f[105]; long long f_len[105]; int k; struct data { long long ans; int l_id, r_id; }; int cnt2[2][2]; int sum2[2][2][MAXN*5]; int cnt[2]; int sum[2][MAXN*3]; inline data operator + (const data &a, const data &b) { data ret; ret.ans = a.ans + b.ans + cnt2[a.r_id][b.l_id] - cnt[a.r_id] - cnt[b.l_id]; ret.l_id = a.l_id; ret.r_id = b.r_id; return ret; } data f_data[105]; inline void init() { init_hash(); cnt[0] = count(f[k - 1], sum[0]); cnt[1] = count(f[k], sum[1]); cnt2[0][0] = count(f[k - 1] + f[k - 1], sum2[0][0]); cnt2[0][1] = count(f[k - 1] + f[k], sum2[0][1]); cnt2[1][0] = count(f[k] + f[k - 1], sum2[1][0]); cnt2[1][1] = count(f[k] + f[k], sum2[1][1]); f_data[k - 1] = (data){cnt[0], 0, 0}; f_data[k] = (data){cnt[1], 1, 1}; int i; for (i = k + 1; i <= 100; i++) { f_data[i] = f_data[i - 1] + f_data[i - 2]; } } int _n[205], _l[205], _r[205]; int _cnt; inline void push(int n, int l, int r) { debug("push %d %d %d\n", n, l, r); ++_cnt; _n[_cnt] = n; _l[_cnt] = l; _r[_cnt] = r; } inline void _query(int n, long long l, long long r) { if (n <= k) { push(n, l, r); return; } if (l == 1 && r == f_len[n]) { push(n, 0, 0); return; } long long t = f_len[n - 1]; if (r <= t) { _query(n - 1, l, r); } else if (l > t) { _query(n - 2, l - t, r - t); } else { _query(n - 1, l, t); _query(n - 2, 1, r - t); } } inline long long query(int n, long long l, long long r) { if (n < k - 1) { return 0; } if (n <= k) { return sum[n - k + 1][r - len_s + 1] - sum[n - k + 1][l - 1]; } _cnt = 0; _query(n, l, r); if (_cnt == 1) { // assert(_n[1] > k); if (_n[1] <= k) { assert(_n[1] >= k - 1); return sum[_n[1] - k + 1][_r[1] - len_s + 1] - sum[_n[1] - k + 1][_l[1] - 1]; } else { return f_data[_n[1]].ans; } } else if (_cnt == 2 && _n[1] <= k && _n[2] <= k) { return sum2[_n[1] - k + 1][_n[2] - k + 1][_r[2] + f_len[_n[1]] - len_s + 1] - sum2[_n[1] - k + 1][_n[2] - k + 1][_l[1] - 1]; } else { long long ret = 0; int L = 1, R = _cnt; if (_n[1] <= k) { // 1, 1-2 // assert(_n[2] > k); ret += cnt2[_n[1] - k + 1][f_data[_n[2]].l_id] - sum2[_n[1] - k + 1][f_data[_n[2]].l_id][_l[1] - 1]; ret -= cnt[f_data[_n[2]].l_id]; L = 2; } if (_n[_cnt] <= k) { // (_cnt-1)-_cnt, _cnt // assert(_n[_cnt - 1] > k); ret += sum2[f_data[_n[_cnt - 1]].r_id][_n[_cnt] - k + 1][_r[_cnt] + f_len[f_data[_n[_cnt - 1]].r_id + k - 1] - len_s + 1]; ret -= cnt[f_data[_n[_cnt - 1]].r_id]; R = _cnt - 1; } int i; for (i = L; i <= R; i++) { // assert(_n[i] > k); ret += f_data[_n[i]].ans; } for (i = L; i < R; i++) { ret += cnt2[f_data[_n[i]].r_id][f_data[_n[i + 1]].l_id]; ret -= cnt[f_data[_n[i]].r_id]; ret -= cnt[f_data[_n[i + 1]].l_id]; } return ret; } } int main() { freopen("str1.in", "r", stdin); freopen("str.out", "w", stdout); scanf("%s", a); scanf("%s", b); scanf("%s", s); len_s = strlen(s); f[0] = a, f[1] = b; int i; for (i = 2; ; i++) { f[i] = f[i - 1] + f[i - 2]; debug("f %d = %s\n",i,f[i].c_str()); if ((int)f[i - 1].length() >= len_s) { break; } } k = i; init(); f_len[0] = f[0].length(); f_len[1] = f[1].length(); for (i = 2; i <= 100; i++) { f_len[i] = f_len[i - 1] + f_len[i - 2]; } scanf("%d", &q); for (i = 1; i <= q; i++) { int n; long long l, r; scanf("%d%I64d%I64d", &n, &l, &r); if (r - l + 1 < len_s) { // cout<<l<<" "<<r<<" "<<r-l+1<<" "<<len_s<<endl; puts("0"); } else { printf("%I64d\n", query(n, l, r)); } } return 0; }
标签:_id 判断 输入输出格式 求和 include mat style bit ensure
原文地址:http://www.cnblogs.com/zzyh/p/7482244.html