标签:6.4 最小化 效果 方法 isp 运行 ack pen top
用于找出不带标签数据的相似性的算法
与广义线性模型和决策树类似,K-Means参 数的最优解也是以成本函数最小化为目标。K-Means成本函数公式如下: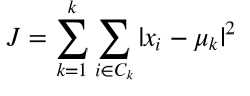
成本函数是各个类畸变程度(distortions)之和。每个类的畸变程度等于 该类重心与其内部成员位置距离的平方和。若类内部的成员彼此间越紧凑则类的畸变程度越小,反 之,若类内部的成员彼此间越分散则类的畸变程度越大。求解成本函数最小化的参数就是一个重复配 置每个类包含的观测值,并不断移动类重心的过程。首先,类的重心是随机确定的位置。实际上,重 心位置等于随机选择的观测值的位置。每次迭代的时候,K-Means会把观测值分配到离它们最近的 类,然后把重心移动到该类全部成员位置的平均值那里。
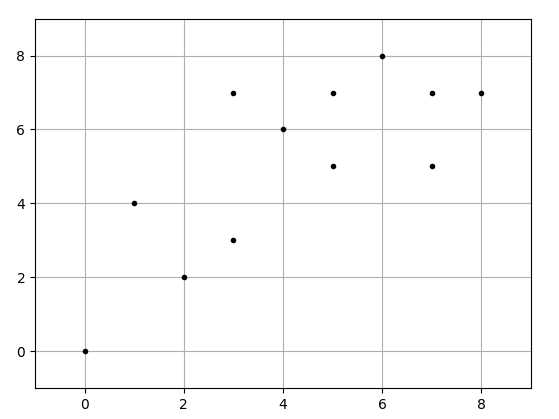
import matplotlib.pyplot as plt from matplotlib.font_manager import FontProperties font = FontProperties(fname=r"C:\Users\Lenovo\Desktop\data_set\msyh.ttc", size=10) ‘‘‘可视化样本点‘‘‘ import numpy as np X0 = np.array([7, 5, 7, 3, 4, 1, 0, 2, 8, 6, 5, 3]) X1 = np.array([5, 7, 7, 3, 6, 4, 0, 2, 7, 8, 5, 7]) plt.figure() plt.axis([-1, 9, -1, 9]) plt.grid(True) plt.plot(X0, X1, ‘k.‘) # plt.show()
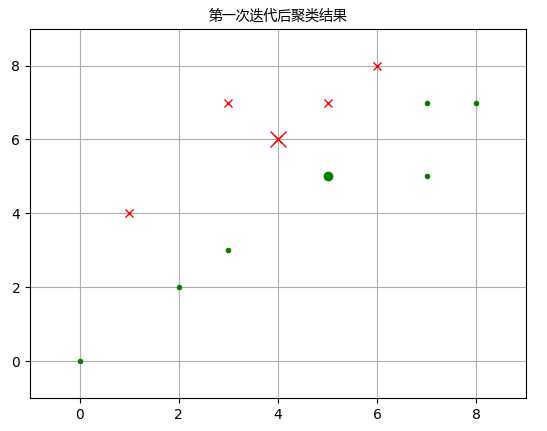
C1 = [1, 4, 5, 9, 11] C2 = list(set(range(12)) - set(C1)) X0C1, X1C1 = X0[C1], X1[C1] X0C2, X1C2 = X0[C2], X1[C2] plt.figure() plt.title(‘第一次迭代后聚类结果‘,fontproperties=font) plt.axis([-1, 9, -1, 9]) plt.grid(True) plt.plot(X0C1, X1C1, ‘rx‘) plt.plot(X0C2, X1C2, ‘g.‘) plt.plot(4,6,‘rx‘,ms=12.0) plt.plot(5,5,‘g.‘,ms=12.0) plt.show()
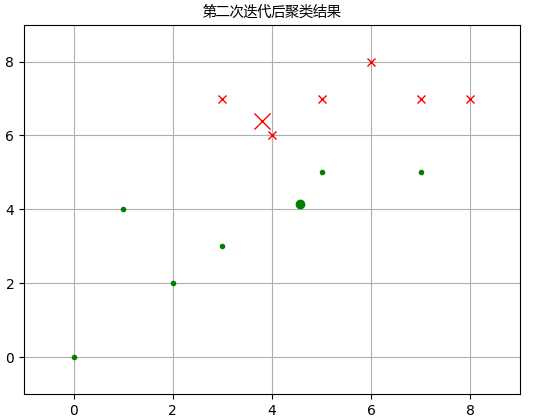
C1 = [1, 2, 4, 8, 9, 11] C2 = list(set(range(12)) - set(C1)) X0C1, X1C1 = X0[C1], X1[C1] X0C2, X1C2 = X0[C2], X1[C2] plt.figure() plt.title(‘第二次迭代后聚类结果‘,fontproperties=font) plt.axis([-1, 9, -1, 9]) plt.grid(True) plt.plot(X0C1, X1C1, ‘rx‘) plt.plot(X0C2, X1C2, ‘g.‘) plt.plot(3.8,6.4,‘rx‘,ms=12.0) plt.plot(4.57,4.14,‘g.‘,ms=12.0) plt.show()
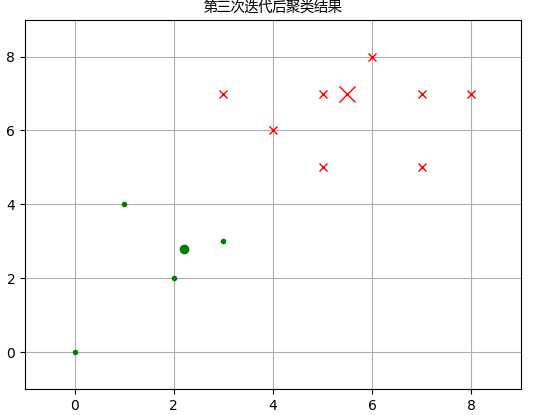
C1 = [0, 1, 2, 4, 8, 9, 10, 11] C2 = list(set(range(12)) - set(C1)) X0C1, X1C1 = X0[C1], X1[C1] X0C2, X1C2 = X0[C2], X1[C2] plt.figure() plt.title(‘第三次迭代后聚类结果‘,fontproperties=font) plt.axis([-1, 9, -1, 9]) plt.grid(True) plt.plot(X0C1, X1C1, ‘rx‘) plt.plot(X0C2, X1C2, ‘g.‘) plt.plot(5.5,7.0,‘rx‘,ms=12.0) plt.plot(2.2,2.8,‘g.‘,ms=12.0) plt.show()
import numpy as np cluster1 = np.random.uniform(0.5, 1.5, (2, 10)) cluster2 = np.random.uniform(3.5, 4.5, (2, 10)) X = np.hstack((cluster1, cluster2)).T # plt.figure() # plt.axis([0, 5, 0, 5]) # plt.grid(True) # plt.plot(X[:,0],X[:,1],‘k.‘) ‘‘‘计算K值从1到10对应的平均畸变程度:‘‘‘ from sklearn.cluster import KMeans from scipy.spatial.distance import cdist K = range(1, 11) # K = list(range(1, 11)) meandistortions = [] for k in K: kmeans = KMeans(n_clusters=k) kmeans.fit(X) meandistortions.append(sum(np.min(cdist(X,kmeans.cluster_centers_,‘euclidean‘), axis=1)) / X.shape[0]) plt.plot(K, meandistortions, ‘bx-‘) plt.xlabel(‘k‘) plt.ylabel(‘平均畸变程度‘,fontproperties=font) plt.title(‘用肘部法则来确定最佳的K值‘,fontproperties=font) plt.show()
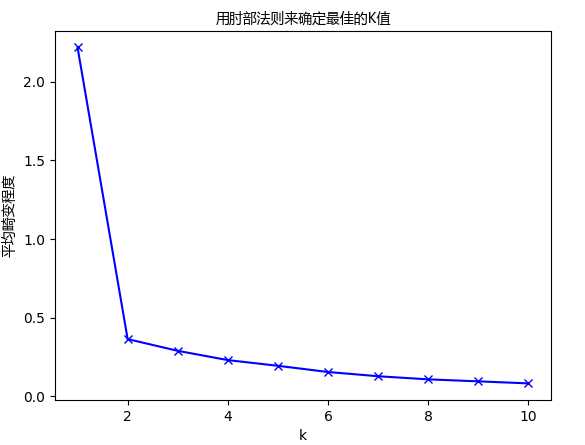
从图中可以看出,K值从1到2时,平均畸变程度变化最大。超过2以后,平均畸变程度变化显著降 低。因此肘部就是K=2.
下面用肘部法则来确定3个类的最佳的K值:
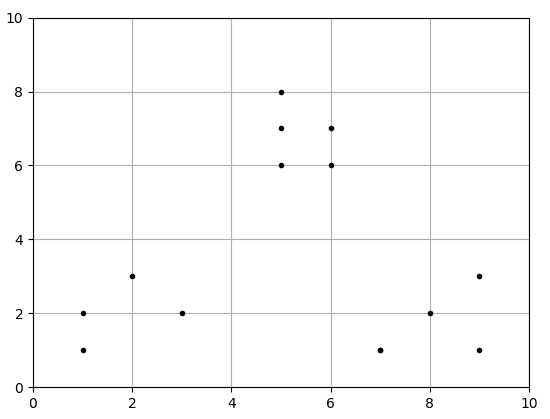
import numpy as np x1 = np.array([1, 2, 3, 1, 5, 6, 5, 5, 6, 7, 8, 9, 7, 9]) x2 = np.array([1, 3, 2, 2, 8, 6, 7, 6, 7, 1, 2, 1, 1, 3]) X = np.array(list(zip(x1, x2))).reshape(len(x1), 2) # print(list(zip(x1, x2))) # print(X) plt.figure() plt.axis([0, 10, 0, 10]) plt.grid(True) plt.plot(X[:,0],X[:,1],‘k.‘) plt.show()
from sklearn.cluster import KMeans from scipy.spatial.distance import cdist K = range(1, 10) meandistortions = [] for k in K: kmeans = KMeans(n_clusters=k) kmeans.fit(X) meandistortions.append(sum(np.min(cdist(X, kmeans.cluster_centers_, ‘euclidean‘), axis=1)) / X.shape[0]) plt.plot(K, meandistortions, ‘bx-‘) plt.xlabel(‘k‘) plt.ylabel(‘平均畸变程度‘,fontproperties=font) plt.title(‘用肘部法则来确定最佳的K值‘,fontproperties=font) plt.show()
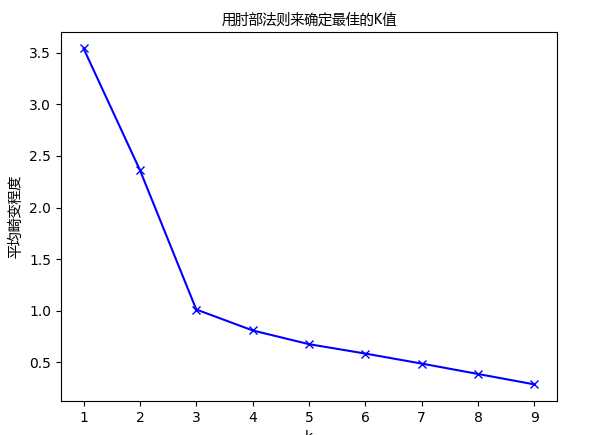
从图中可以看出, 值从1到3时,平均畸变程度变化最大。超过3以后,平均畸变程度变化显著降低。因此肘部就是 。
计算公式如下: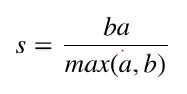
a是每一个类中样本彼此距离的均值,b 是一个类中样本与其最近的那个类的所有样本的距离的均 值。下面的例子运行四次K-Means,从一个数据集中分别创建2,3,4,5,8个类,然后分别计算它们 的轮廓系数。
import matplotlib.pyplot as plt from matplotlib.font_manager import FontProperties font = FontProperties(fname=r"C:\Users\Lenovo\Desktop\data_set\msyh.ttc", size=10) import numpy as np from sklearn.cluster import KMeans from sklearn import metrics plt.figure(figsize=(6, 6)) plt.subplot(3, 2, 1) x1 = np.array([1, 2, 3, 1, 5, 6, 5, 5, 6, 7, 8, 9, 7, 9]) x2 = np.array([1, 3, 2, 2, 8, 6, 7, 6, 7, 1, 2, 1, 1, 3]) X = np.array(list(zip(x1, x2))).reshape(len(x1), 2) plt.xlim([0, 10]) plt.ylim([0, 10]) plt.title(‘样本‘,fontproperties=font) plt.scatter(x1, x2) colors = [‘b‘, ‘g‘, ‘r‘, ‘c‘, ‘m‘, ‘y‘, ‘k‘, ‘b‘] markers = [‘o‘, ‘s‘, ‘D‘, ‘v‘, ‘^‘, ‘p‘, ‘*‘, ‘+‘] tests = [2, 3, 4, 5, 8] subplot_counter = 1 for t in tests: subplot_counter += 1 plt.subplot(3, 2, subplot_counter) kmeans_model = KMeans(n_clusters=t).fit(X) ‘‘‘kmeans_model.labels_获取索引及对应的类别‘‘‘ for i, l in enumerate(kmeans_model.labels_): plt.tight_layout() #用来调整子图间距 plt.plot(x1[i], x2[i], color=colors[l], marker=markers[l],ls=‘None‘) plt.xlim([0, 10]) plt.ylim([0, 10]) plt.title(‘K = %s, 轮廓系数 = %.03f‘ % (t, metrics.silhouette_score(X, kmeans_model.labels_, metric=‘euclidean‘)), fontproperties=font) plt.show()
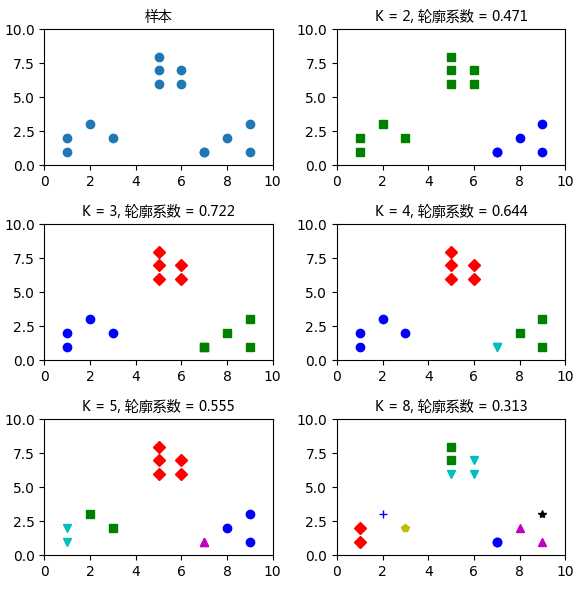
很显然,这个数据集包括三个类。在K=3 的时候轮廓系数是最大的。在 K=8的时候,每个类的 样本不仅彼此很接近,而且与其他类的样本也非常接近,因此这时轮廓系数是最小的。
Re:如果是高维就要通过降维可视化分析
标签:6.4 最小化 效果 方法 isp 运行 ack pen top
原文地址:http://www.cnblogs.com/JueJi-2017/p/7487419.html