标签:node rect ret turn ber get problem input oss
| Time Limit: 1000MS | Memory Limit: 65536K | |
| Total Submissions: 2302 | Accepted: 1056 |
Description
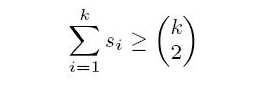
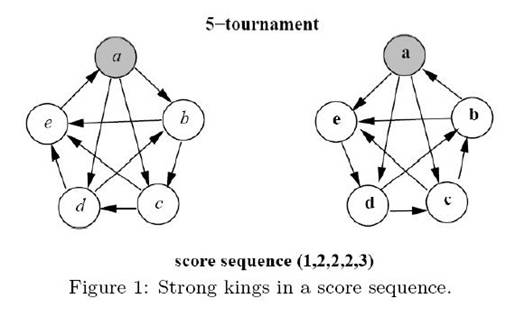
Input
Output
Sample Input
5 1 2 2 2 3 1 1 3 4 4 4 4 3 3 4 4 4 4 5 6 6 6 0 3 4 4 4 5 5 5 6 0 3 3 3 3 3
Sample Output
2 4 5 3 5
神奇的构图
把每个人和每场比赛看成两种点
源点向每个人连,cap为其得分
每场比赛向汇点连,cap为1
#include<cstdio> #include<cstring> #include<algorithm> using namespace std; const int N=1808; int head[N],tot,S,T; int q[N],dis[N],n,sc[12]; struct node { int next,v,w; } e[N]; void add(int u,int v,int w) { e[tot].v=v; e[tot].w=w; e[tot].next=head[u]; head[u]=tot++; } bool bfs() { memset(dis,-1,sizeof(dis)); dis[S]=0; int l=0,r=0; q[r++]=S; while(l<r) { int u=q[l++]; for(int i=head[u]; ~i; i=e[i].next) { int v=e[i].v; if(dis[v]==-1&&e[i].w>0) { q[r++]=v; dis[v]=dis[u]+1; if(v==T) return true; } } } return false; } int dfs(int s,int low) { if(s==T||!low) return low; int ans=low,a; for(int i=head[s]; ~i; i=e[i].next) { if(e[i].w>0&&dis[e[i].v]==dis[s]+1&&(a=dfs(e[i].v,min(e[i].w,ans)))) { e[i].w-=a; e[i^1].w+=a; ans-=a; if(!ans) return low; } } if(low==ans) dis[s]=-1; return low-ans; } bool Ju(int x){ tot=0; memset(head,-1,sizeof(head)); for(int i=0;i<n;++i) add(S,i+1,sc[i]),add(i+1,S,0); for(int i=n+1;i<=(n*n+n)/2;++i) add(i,T,1),add(T,i,0); int pos[15][15],tc=n+1; for(int i=1;i<=n;++i) for(int j=i+1;j<=n;++j) pos[i][j]=pos[j][i]=tc++; for(int i=1;i<x;++i) for(int j=i+1;j<=n;++j) { add(i,pos[i][j],1),add(pos[i][j],i,0); add(j,pos[i][j],1),add(pos[i][j],j,0); } for(int i=x;i<=n;++i) for(int j=i+1;j<=n;++j) { add(i,pos[i][j],1),add(pos[i][j],i,0); if(sc[i-1]==sc[j-1]) add(j,pos[i][j],1),add(pos[i][j],j,0); } int ans=0; while(bfs()) ans+=dfs(S,10086); return ans==n*(n-1)/2; } int main(){ int Ta; for(scanf("%d ",&Ta);Ta--;){ char str[108]; gets(str); int len=strlen(str); n=(len+1)/2; if(n==1) {puts("1");continue;} S=0,T=(n*n+n)/2+1; for(int i=0;i<len;i+=2) sc[i>>1]=str[i]-‘0‘; int l=1,r=n,ans=1; sort(sc,sc+n); while(l<=r){ int mid=(l+r)>>1; if(Ju(mid)) {r=mid-1;ans=n-mid+1;} else l=mid+1; } printf("%d\n",ans); } }
标签:node rect ret turn ber get problem input oss
原文地址:http://www.cnblogs.com/mfys/p/7489051.html