标签:pac upload logs oat 序号 cdn false bool 很多
蒟蒻HansBug在化学考场上,挠了无数次的头,可脑子里还是一片空白。
眼下出现在蒟蒻HansBug面前的是一个化学合成题,据他所知,一般答案如下面这样的格式:
 (接下一行)
(接下一行)

简单解释下:每种化合物可以通过一步反应生成另一个化合物(将这称作一步反应,设为 A--->B),现在假设每个A--->B中,理论上1个单位的A都仅可以生成1个单位的B。然而实际实验表明,并不存在绝对完全的化学转化,设转化率为C(即1个单位A实际可以生成C个单位的B,0<C<1)。
现在蒟蒻HansBug的知识体系中有N个这样A--->B的转化。然而题目中蒟蒻HansBug要由1个单位的化合物S生成化合物T,可是他脑细胞和RP已经消耗殆尽,所以找到最终产量最高的合成路线的艰巨任务就交给你啦!
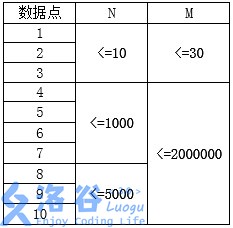
第一行为4个整数:N、M、S、T,分别表示总共出现的化合物个数、HansBug所知道的反应个数、起始的化合物序号、终末的化合物序号。(1<=S、T<=N)
第2-M+1行每行为两个整数和一个实数:Ai、Bi、Ci,分别表示第i个反应为由1个单位的Ai化合物生成Ci单位的Bi化合物。
一行,包含一个实数,为最佳路线下最终的产量(四舍五入保留4位小数),如果没有可行路线的话,输出orz。
3 3 1 3 1 3 0.8 1 2 0.9 2 3 0.9
0.8100
3 3 2 1
1 3 0.8
1 2 0.9
2 3 0.9
orz
样例1和样例2中,两条合成路线分别为1--->3、1--->2、2--->3,产率分别为0.8、0.9、0.9。
在样例1中,有两种可行的路线1--->3和1--->2--->3,最终产量分别为0.8、0.9*0.9=0.81,故第二条路线更优,产量为0.8100。
样例2中,2只能生成3,3无法生成别的化合物,故无法生成,蒟蒻HansBug只好选择orz。
样例数据:
和求最短路/最长路比较相似。
Spfa/Dijstra随便糊一下就好了。
点数n<=5000,所以用邻接表通常会快很多。
我用的是Spfa,因为我想练练Spfa,但由于我对它不太熟悉,做这道题的时候TLE了好几次,后来才弄好的。
后来看了一下题解,提到有链式前向星这种神奇的表示方法,我也学到了一点。
顺便一说,我好像被卡Vector和Queue了....
#include <cstdio> using namespace std; int head[5005]; struct Node{ int to, next; float v; }; Node w[2000005]; int wtop=5001; float dis[5005]; int spfa[20005], sl=1, sr=0; bool visited[5005]; int main(){ int i, j; int n, m, s, e; int a, p; //初始化head for(i=1; i<=5000; i++) head[i]=i; scanf("%d %d %d %d", &n, &m, &s, &e); for(i=1; i<=m; i++){ scanf("%d", &a); scanf("%d %f", &w[head[a]].to, &w[head[a]].v); w[head[a]].next=wtop; head[a]=wtop; wtop++; } dis[s]=1; spfa[++sr]=s; while(sl<=sr){ a=spfa[sl]; sl++; p=a; while(p^head[a]){ if(dis[a]*w[p].v > dis[w[p].to]){ dis[w[p].to]=dis[a]*w[p].v; if(!visited[w[p].to]) spfa[++sr]=w[p].to; visited[w[p].to]=true; } p=w[p].next; } visited[a]=false; } if(dis[e]) printf("%.4f", dis[e]); else printf("orz"); return 0; }
【洛谷P2784·图论·Spfa】化学1(chem1)- 化学合成
标签:pac upload logs oat 序号 cdn false bool 很多
原文地址:http://www.cnblogs.com/cutemaru/p/7489302.html