标签:不同 href 部分 active anaconda 交互式 nbsp scale 0.00
推荐使用Anaconda作为python环境,可以避免大量的兼容性问题
以在服务器上安装为例(linux)
1.在anaconda官网上下载与自己机器对应的版本 下载.sh形式的文件
2.在anaconda下载目录中输入以下路径(下载的文件名可能不同)
$ bash Anaconda-4.2.0-Linux-x86_64.sh
3. 安装tensorflow-cpu版本 如果要安装gpu,请跳到第4步
推荐安装编译好的release版本,装起来比较简单 也就是直接用网上的已经编译好的.whl文件
$ pip install --upgrade https://storage.googleapis.com/tensorflow/linux/cpu/tensorflow-1.0.0rc0-cp35-cp35m-linux_x86_64.whl
后面的网址可以到网上找相应的版本进行替换
4. 安装tensorflow-gpu版本
需要预先安装显卡驱动,CUDA和cuDNN
CUDA的安装包里一般集成了显卡驱动,直接在官网下载 CUDA下载 下载.run文件
注意:安装之前先看下网上已经编译好的tensorflow-gpu支持的CUDA和cuDNN的具体版本再安装,这样之后就不会出现不兼容的问题
安装CUDA:
$ chmod u+x cuda_8.0.44_linux.run $ sudo ./cuda_8.0.44_linux.run
在安装过程中根据提示可以自己设置安装路径,一般可以选择不安装CUDA samples,因为只是通过tensorflow调用cuda,并不需要写cuda代码
安装cuDNN:
官网下载.tgz压缩包, 并到下载路径,输入命令
$ sudo tar -xzvf cudnn-8.0-linux-x64-v5.1.tgz
通常是要把cuDNN的文件里的内容全部复制到cuda-8.0的相应目录下
设置系统环境中CUDA路径:
$ vim ~/.bashrc 在文件底部加入 export LD_LIBRARY_PATH=/usr/local/cuda08.0/lib64:/usr/local/cuda-8.0/extras/CUPTI/lib64:$LD_LIBRARY_PATH export CUDA_HOME=/usr/local/cuda-8.0 export PATH=/usr/local/cuda-8.0/bin:$PATH 保存退出 $source ~/.bashrc
安装tensorflow-gpu:
同样推荐安装编译好的release版本,一步到位
pip install --upgrade https://storage.googleapis.com/tensorflow/linux/gpu/tensorflow_gpu-1.0.0rc0-cp35-cp35m-linux_x86_64.whl
1. 下载MNIST数据:
from tensorflow.examples.tutorials.mnist import input_data mnist = input_data.read_data_sets("MNIST_data/",one_hot=True)
MNIST数据集是28x28像素的图像,这里为了简便,拉伸成一个784维的特征
共有55000张训练图片,所以训练数据特征是一个55000x784的tensor
label是55000x10的tensor, 每一个样本的label是相应的one-hot表示
2. 分类模型选择softmax regression的算法,常用于多分类任务
对于后面的CNN和RNN,如果是分类模型,最后一层同样是softmax regression,用于对每个类别进行估算概率
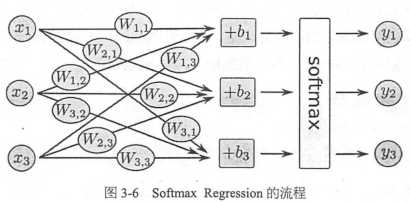
每个类别都有自己的一套W和b, b表示数据本身的一些倾向,比如大部分数字都是0,那么0对应的bias会很大
import tensorflow as tf sess = tf.InteractiveSession() #将这个session注册为默认的session x = tf.placeholder(tf.float32,[None,784]) #输入数据 W = tf.Variable(tf.zeros(784,10])) b = tf.Variable(tf.zeros([10]) y = tf.nn.softmax(tf.matmul(x,W)+b)
tf.nn包含了大量神经网络组件,tensorflow最厉害的地方不是定义公式,而是将forward和backword的内容都自动实现(无论是CPU或者GPU),只要接下来定义好loss,训练时将会自动求导并进行梯度下降,完成对softmax regression模型参数的自动学习
3.定义loss function
对于多分类问题,通常使用cross-entropy作为loss function
y_ = tf.placeholder(tf.float32,[None,10]) #输入正确的label cross_entropy = tf.reduce_mean(-tf.reduce_sum(y_ * tf.log(y), reduction_indices=[1]))
这里的*是element-wise乘法,只是选出正确标签位置的相应预测概率, reduction_indices=[1]是按行加和,最后再reduce_mean对所有样本的loss做平均
4.定义优化算法进行自动求解
train_step = tf.train.GradientDescentOptimizer(0.5).minimize(cross_entropy)
全局初始化参数:
tf.global_variables_initializer().run()
只要定义了variables,就一定要有这么一句,位置就放在所有变量定义之后
5.进行迭代训练
这里每次都随机从训练集中抽取100条样本高层一个mini-batch,并feed给placeholder,然后调用train_step对这些样本进行训练
for i in range(1000): batch_xs, batch_ys = mnist.train.next_batch(100) train_step.run({x:batch_xs, y_:batch_ys})
完成了训练,就可以对模型的准确率进行验证
correct_prediction= tf.equal(tf.argmax(y,1),tf.argmax(y_,1)) accuracy = tf.reduce_mean(tf.cast(correct_prediction,tf.float32)) print(accuracy.eval({x:mnist.test.images,y_:mnist.test.labels}))
tf.argmax是寻找一个向量中最大值的序号,1表示是按行找每行最大值的下标
tf.equal则是判断预测的数字类别是否就是正确的类别,返回的是True,False矩阵
tf.cast是把True,False投射到实数上,比如True表示1,False表示0
然后tf.reduce_mean是计算所有样本中预测正确样本所占的比例
其实上面correct_prediction和accuracy都是定义的计算图中的两个节点,并没有实际计算它们的输出结果
所以第三行代码accuracy.eval(feed_dict={x:mnist.test.images,y_:mnist.test.labels})才是真正的运行计算图
注意这里是因为使用了交互式的接口sess = tf.InteractiveSession()
所以这里可以用node.run(feed_dict={})运行节点,node.eval(feed_dict={})计算输出值 其他方法的话需要用sess.run(node,feed_dict={})
以上的这个简单的算法可以达到92%的精确度,所以说神经网络的效果很惊人
定义的各个公式其实就是计算图,在执行这行代码时,计算还没实际发生,只有等调用run方法,并feed数据时计算才真正执行
比如cross_entropy,train_step,accuracy等都是计算图中的节点,不是数据结构,只有通过run方法执行这些节点才能得到计算结果
深度学习是一种无监督的特征学习,模仿了人脑的对特征逐层抽象提取的过程
早年学者研究稀疏编码时,收集了大量黑白风景照,并提取了许多16x16的图像碎片,他们发现几乎所有图像碎片都可以有64种正交边组合得到,而且组合一张图像碎片所需要的边的数量是很少的,即稀疏的。同样声音也存在这种现象,绝大多数声音可以有一些基本结构线性组合得到,这其实就是特征的稀疏表达,使用少量的基本特征组合拼接得到更高层抽象的特征。多层神经网络中前一层的输出都是未加工的项数,后一层则是对像素进行加工组织成更高阶的特征(即前面提到的将边组合成图像碎片)
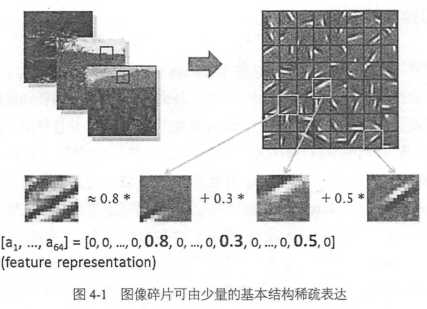
对于没有标注的数据,可以使用无监督的自编码器来提取特征
自编码器也是一种神经网络,它的输入和输出是一致的,借助稀疏编码的思想,目标是使用稀疏的一些高阶特征重新组合来重构自己
特点:
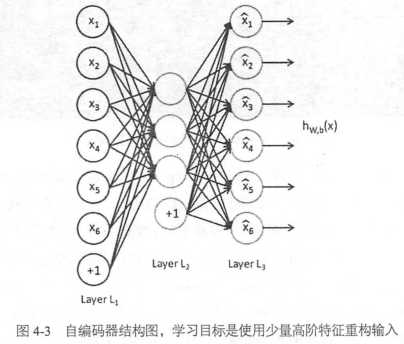
实现的是去噪自编码器,给输入加上高斯加性噪声,希望输出原数据
用scikit-learn中的preprocessing模块对数据进行预处理
import numpy as np import sklearn.preprocessing as prep imiport tensorflow as tf from tensorflow.examples.tutorials.mnist import input_data
参数初始化方法xavier initialization,根据某一层网络中的输入输出节点数量自动调整为最合适的分布,满足0均值,方差为2/(Nin+Nout),分布可以为均匀分布或者高斯分布
下面代码设置的均匀分布,可以用公式计算方差D(x) = (max-min)^2/12 = 2/(Nin+Nout)
def xavier_init(fan_in,fan_out,constant=1): low = -constant * np.sqrt(6.0/(fan_in+fan_out)) high = constant * np.sqrt(6.0/(fan_in+fan_out)) return tf.random_uniform((fan_in,fan_out),minval=low,maxval=high,dtype=tf.float32)
下面定义一个去噪自编码器的class
class AdditiveGaussianNoiseAutoencoder(object): def __init__(self,n_input,n_hidden,transfer_function=tf.nn.softplus, optimizer=tf.train.AdamOptimizer(),scale=0.1): # initialize the parameters self.n_input = n_input self.n_hidden = n_hidden self.transfer = transfer_function self.scale = tf.placeholder(tf.float32) self.training_scale = scale network_weights = self._initialize_weights() self.weights = network_weights # define the network architecture self.x = tf.placeholder(tf.float32,[None,self.n_input]) self.hidden = self.transfer(tf.add(tf.matmul( self.x + scale * tf.random_normal((n_input,)), self.weights[‘w1‘]),self.weights[‘b1‘])) self.reconstruction = tf.add(tf.matmul(self.hidden, self.weights[‘w2‘]),self.weights[‘b2‘]) # define loss function self.cost = 0.5 * tf.reduce_sum(tf.pow(tf.subtract( self.reconstruction,self.x),2.0)) self.optimizer = optimizer.minimize(self.cost) # run the session init = tf.global_variables_initializer() self.sess = tf.Session() self.sess.run(init) # define initialization function def _initialize_weights(self): all_weights = dict() all_weights[‘w1‘] = tf.Variable(xavier_init(self.n_input,self.n_hidden)) all_weights[‘b1‘] = tf.Variable(tf.zeros([self.n_hidden],dtype=tf.float32)) # reconstruction layer has no activate function, so can initialized by zero all_weights[‘w2‘] = tf.Variable(tf.zeros([self.n_hidden,self.n_input],dtype=tf.float32)) all_weights[‘b2‘] = tf.Variable(tf.zeros([self.n_input],dtype = tf.float32)) return all_weights # define a train step with a batch def partial_fit(self,X): cost, opt = self.sess.run((self.cost,self.optimizer), feed_dict = {self.x:X, self.scale:self.training_scale}) return cost # calculate the total cost def calc_total_cost(self,X): return self.sess.run(self.cost, feed_dict={self.x:X, self.scale:self.training_scale}) # output the hidden state of the data def transform(self,X): return self.sess.run(self.hidden,feed_dict={self.x:X, self.scale:self.training_scale}) # reconstruct data by the hidden state def generate(self,hidden=None): if hidden is None: hidden = np.random.normal(size=self.weights[‘b1‘]) return self.sess.run(self.reconstruction,feed_dict = {self.hidden:hidden}) # transform + generate input original data, output reconstructed data def reconstruct(self,X): return self.sess.run(self.reconstruction,feed_dict={self.x:X,self.scale:self.training_scale}) def getWeights(self): return self.sess.run(self.weights[‘w1‘]) def getBiases(self): return self.sess.run(self.weights[‘b1‘])
去噪自编码器的class定义如上,其中包括神经网络的设计,权重的初始化以及常用的成员函数
接下来用定义好的AGN自编码器在MNIST数据集上进行一些测试看数据复原的效果如何
mnist = input_data.read_data_sets(‘MNIST_data‘,one_hot=True) # preprocess the data as 0-mean 1-std distribution # train and test should use the same scaler def standard_scale(X_train,X_test): preprocessor = prep.StandardScaler().fit(X_train) X_train = preprocessor.transform(X_train) X_test = preprocessor.transform(X_test) return X_train, X_test # define no return sampling function with a batch def get_random_block_from_data(data,batch_size): start_index = np.random.randint(0,len(data)-batch_size) return data[start_index:(start_index+batch_size)] X_train,X_test = standard_scale(mnist.train.images,mnist.test.images)
以上定义了两个函数,一个是用来标准化数据的函数,将数据标准化到0均值,标准差为1的分布
第二个函数就是获取一个随机的batch_size大小block的数据,下面是实例测试:
# define parameters n_samples = int(mnist.train.num_examples) training_epochs = 20 batch_size = 128 display_step = 1 autoencoder = AdditiveGaussianNoiseAutoencoder(n_input=784, n_hidden=200,transfer_function=tf.nn.softplus, optimizer=tf.train.AdamOptimizer(learning_rate=0.001), scale=0.01) for epoch in range(training_epochs): avg_cost = 0. total_batch = int(n_samples/batch_size) for i in range(total_batch): bach_xs = get_random_block_from_data(X_train,batch_size) cost = autoencoder.partial_fit(batch_xs) avg_cost += cost / n_samples * batch_size if epoch % display_step == 0: print("Epoch:", ‘%04d‘ %(epoch+1),"cost=","{:.9f}".format(avg_cost)) print("total cost: "+str(autoencoder.calc_total_cost(X_test)))
运行结果如下:
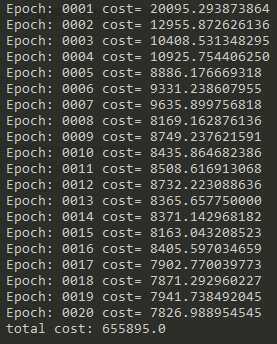
可以看到通过迭代,loss逐渐降低,说明还原效果逐渐变好
总结:
自编码器作为一种无监督学习的方法,它与其他无监督学习的主要不同在于,它不是对数据进行聚类,而是提取其中最有用,最频繁出现的额高阶特征,根据这些高阶特征重构数据。
有理论研究表明,为了拟合复杂函数需要的隐含节点的数目,基本上随着隐含层的书领真多呈指数下降趋势,也就是说层数越多,神经网络所需要的隐含节点可以越少,这也是深度学习的特点之一,层数越深,概念越抽象,需要背诵的知识点(神经网络隐含节点)就越少。
过拟合意味着泛化性能不好,模型只是记忆了当前数据的特征,不具备推广能力,通过dropout的方式可以防止过拟合,随机丢弃层中的节点,表示丢弃了某些特征,也是一种bagging的思想,我们可以理解为每次丢弃节点数据都是对特征的一种采样。相当于我们训练了一个ensemble的神经网络模型,对每个样本都做特征采样。
参数难以调试也是一个大问题,有理论表示,神经网络可能有很多个局部最优解都可以达到比较好的分类效果,而全局最优反而容易是过拟合的解
对SGD,一开始我们希望学习速率大一些,可以加速收敛,但是训练的后期又希望学习速率可以小一点,这里可以比较稳定地落入一个局部最优解,不同的机器学习问题所需要的学习速率也不太好设置,需要反复调试,因此就有像Adagrad,Adam,Adadelta等自适应的方法可以减轻调试参数的负担
from tensorflow.examples.tutorials.mnist import input_data import tensorflow as tf mnist = input_data.read_data_sets("MNIST_data/",one_hot=True) sess = tf.InteractiveSession() in_units = 784 h1_units = 300 W1 = tf.Variable(tf.truncated_normal([in_units,h1_units],stddev=0.1)) b1 = tf.Variable(tf.zeros([h1_units])) W2 = tf.Variable(tf.zeros([h1_units,10])) b2 = tf.Variable(tf.zeros([10])) x = tf.placeholder(tf.float32,[None,in_units]) keep_prob = tf.placeholder(tf.float32)
下面定义网络结构,比之前的softmax模型多了一个隐含层
# define network structure hidden1 = tf.nn.relu(tf.matmul(x,W1)+b1) hidden1_drop = tf.nn.dropout(hidden1,keep_prob) y = tf.nn.softmax(tf.matmul(hidden1_drop,W2)+b2) #define loss y_ = tf.placeholder(tf.float32,[None,10]) cross_entropy = tf.reduce_mean(-tf.reduce_sum(y_ * tf.log(y),reduction_indices=[1])) train_step = tf.train.AdagradOptimizer(0.3).minimize(cross_entropy)
在训练的时候,输入dropout参数,keep_prob表示保留结点的占比,其余置0
注意在测试过程中不要进行dropout,所以keep_prob设为1
tf.global_variables_initializer().run() for i in range(3000): batch_xs,batch_ys = mnist.train.next_batch(100) train_step.run({x:batch_xs,y_:batch_ys,keep_prob:0.75}) correct_prediction= tf.equal(tf.argmax(y,1),tf.argmax(y_,1)) accuracy = tf.reduce_mean(tf.cast(correct_prediction,tf.float32)) print(accuracy.eval({x:mnist.test.images,y_:mnist.test.labels,keep_prob:1.0}))
测试结果:
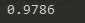
仅仅是加了一层隐含层,精确度就由92%到98%,课件多层神经网络的效果有多显著,同时也使用了一些trick来进行辅助,比如dropout,adagrad,relu等,但是起决定性作用的还是隐含层本身,它能对特征进行抽象和转化
没有隐含层的softmax regression只能直接从图像的额像素点推断是哪个数字,而没有特征抽象的过程。多层神经网络依靠隐含层,这可以组合出高阶特征,比如横线,竖线,圆圈等,之后可以将这些高阶特征或者说组件再组合成数字,就能实现精准地匹配和分类。隐含层输出的高阶特征经常是可以复用额,所以每一类的判别,概率输出都共享这些高阶特征,而不是个字连接独立的高阶特征
标签:不同 href 部分 active anaconda 交互式 nbsp scale 0.00
原文地址:http://www.cnblogs.com/lainey/p/7477646.html