标签:load turn repeat form str amp imu ber second
Where do odds begin, and where do they end? Where does hope emerge, and will they ever break?
Given an integer sequence a1, a2, ..., an of length n. Decide whether it is possible to divide it into an odd number of non-empty subsegments, the each of which has an odd length and begins and ends with odd numbers.
A subsegment is a contiguous slice of the whole sequence. For example, {3, 4, 5} and {1} are subsegments of sequence {1, 2, 3, 4, 5, 6}, while {1, 2, 4} and {7} are not.
The first line of input contains a non-negative integer n (1 ≤ n ≤ 100) — the length of the sequence.
The second line contains n space-separated non-negative integers a1, a2, ..., an (0 ≤ ai ≤ 100) — the elements of the sequence.
Output "Yes" if it‘s possible to fulfill the requirements, and "No" otherwise.
You can output each letter in any case (upper or lower).
3
1 3 5
Yes
5
1 0 1 5 1
Yes
3
4 3 1
No
4
3 9 9 3
No
In the first example, divide the sequence into 1 subsegment: {1, 3, 5} and the requirements will be met.
In the second example, divide the sequence into 3 subsegments: {1, 0, 1}, {5}, {1}.
In the third example, one of the subsegments must start with 4 which is an even number, thus the requirements cannot be met.
In the fourth example, the sequence can be divided into 2 subsegments: {3, 9, 9}, {3}, but this is not a valid solution because 2 is an even number.
题意:给定一数组,判断是否可以分成奇数个组,每组个数是奇数,每组的首尾都为奇数。
分析:偶数长度不可能,奇数长度无论怎么分,首尾必须都为奇数,否则不可能,思维题!
#include <bits/stdc++.h> using namespace std; const int maxn = 105; int a[maxn]; int main() { int n; scanf("%d",&n); for(int i = 0; i < n; i++) scanf("%d",&a[i]); if(n%2==1) { if(a[0]%2==0||a[n-1]%2==0) puts("No"); else puts("Yes"); } else { puts("No"); } return 0; }
Connect the countless points with lines, till we reach the faraway yonder.
There are n points on a coordinate plane, the i-th of which being (i, yi).
Determine whether it‘s possible to draw two parallel and non-overlapping lines, such that every point in the set lies on exactly one of them, and each of them passes through at least one point in the set.
The first line of input contains a positive integer n (3 ≤ n ≤ 1 000) — the number of points.
The second line contains n space-separated integers y1, y2, ..., yn ( - 109 ≤ yi ≤ 109) — the vertical coordinates of each point.
Output "Yes" (without quotes) if it‘s possible to fulfill the requirements, and "No" otherwise.
You can print each letter in any case (upper or lower).
5
7 5 8 6 9
Yes
5
-1 -2 0 0 -5
No
5
5 4 3 2 1
No
5
1000000000 0 0 0 0
Yes
In the first example, there are five points: (1, 7), (2, 5), (3, 8), (4, 6) and (5, 9). It‘s possible to draw a line that passes through points 1, 3, 5, and another one that passes through points 2, 4 and is parallel to the first one.
In the second example, while it‘s possible to draw two lines that cover all points, they cannot be made parallel.
In the third example, it‘s impossible to satisfy both requirements at the same time.
题意:
给定 n 个点的坐标,判断是否所有的点,都在两条不重合的平行线上。
分析:
计算几何很少接触,但是一般CF的计算几何都是考思维,感觉很复杂,情况很多!
看了大牛的思路,确实厉害。
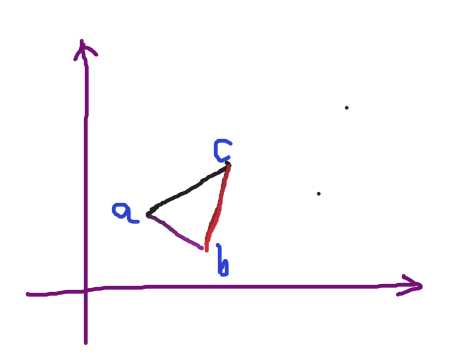
因为只存在两条平行直线,枚举这平行直线,平行直线可以通过ab,bc,ac,另一个点就在另一条平行的直线上。
这样将所有点分为了两个部分,其中另一个部分,要么只有一个点,要么在一条直线上,并且平行。
#include <bits/stdc++.h> using namespace std; const int maxn = 1005; typedef long long ll; int n; struct Node { ll x,y; } nodes[maxn],pp[maxn]; ll cc(Node a,Node b,Node c) { return (b.y-a.y)*(c.x-b.x) - (c.y-b.y)*(b.x-a.x); } bool check() { int cnt=0; for(int i=3; i<=n; i++) if(cc(nodes[1],nodes[2],nodes[i])!=0) pp[++cnt]=nodes[i]; for(int i=3; i<=cnt; i++) if(cc(pp[1],pp[2],pp[i])!=0) return 0; Node ta,tb,tc; ta.x=nodes[2].x-nodes[1].x,ta.y=nodes[2].y-nodes[1].y; tb.x=pp[2].x-pp[1].x,tb.y=pp[2].y-pp[1].y; tc.x=tc.y=0; return cnt<2||cc(tc,ta,tb)==0; } int main() { scanf("%d",&n); for(int i = 1; i <= n; i++) { scanf("%I64d",&nodes[i].y); nodes[i].x = i; } int ff = 0; for(int i=3; i<=n&&!ff; i++) if(cc(nodes[i-2],nodes[i-1],nodes[i])!=0) ff=1; if(!ff) { printf("NO\n"); return 0; } if(check()) { printf("YES\n"); return 0; } swap(nodes[1],nodes[3]); if(check()) { printf("YES\n"); return 0; } swap(nodes[2],nodes[3]); if(check()) { printf("YES\n"); return 0; } printf("NO\n"); return 0; return 0; }
Codeforces Round #431 (Div. 2)
标签:load turn repeat form str amp imu ber second
原文地址:http://www.cnblogs.com/TreeDream/p/7496257.html