标签：整数   ffffff   str   mil   logs   strong   enter   center   5.5   

欧拉函数

2017-09-08

什么是欧拉函数?就是φ(x),定义:φ(x)是小于x的所有1<=a_i<=x且gcd(a_i,x)=1的数的个数;

性质:φ(x)<=x-1(当且x为素数是取等号)即当x为素数时φ(x)=x-1

如果n,m都是质数,那么φ(n*m)=φ(n)*φ(m)=(n-1)(m-1);

如果x为奇数,那么φ(2x)=φ(x);这个其实用简单的代换就知道,φ(2x)=φ(2)*φ(x);φ(2)=1。。这么水......

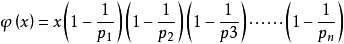即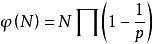

　　p是每一步分解出的质数,n最大为sqrt(x),且max(n)<log₂n

φ(p^k)=p^k-p^k-1=(p-1)*p^k-1①其中p是质数

证明;在0<=a_i<=p^k中有p^k-1个a_i%p=0的数,用容斥即可得到。①得证

 a^φ(x)≡1 (mod x)当x为质数是即为费马小定理..

EXT欧拉函数

 a^x ≡a^{x%φ(m)+φ(m)}(mod m)a为任意整数,x>=φ(m);a与m不一定互素

c^ccccai≡?(mod p)是多少呢,不妨设ai=x,然后从最上层抽一个φ

c^x≡c^{x%φ(p)+φ(p)}(mod p)②,现在再令d=c^x

c^d=c^cx≡c^{(d%φ(p)+φ(p))}(mod p),这就发现了一样的东西..

单独看上面,令p=φ(p),就和②一样了

c^ccc.....变成c^{cc....x%φ(x)+φ(x)}>一堆c的c次幂最后剩一个φ(2)=1,所以在最多log₂次就会得到1,它的值就不会变了

欧拉函数

标签：整数   ffffff   str   mil   logs   strong   enter   center   5.5   

原文地址：http://www.cnblogs.com/ck666/p/7496540.html