标签:near plot 测试数据 通过 dataset 代码 数值 红色 curl
这边文章主要介绍线性回归算法,回归也属于监督算法的范畴,其目标变量是连续数值型,目的是预测数值型的目标值,直观理解就是依据输入写出一个目标值的计算公式,该公式叫为回归方程,而求回归系数的过程就是回归。线性回归是回归算法中最常见的一种。
假设输入数据为$f(x) = w_{1}x_{1}+w_{2}x_{2}+ ......+w_{d}x_{d}+b$
一般用向量写成 $f(x) = w^{T}x+b$
那么,若给定了一些数据点(x, y),怎样才能找到回归系数w呢?一般用的方法是使平方误差最小,而平方误差为 $\sum_{i=1}^{m}(y_{i}-w^{T}x_{i})^{2}$ 要求上式的最小值,对w求导,接着另求导结果为0,
解得满足上述条件下w的计算式: $w = {({X}^{T}X)}^{-1}{X}^{T}y$ 下面用Python给出例子说明线性回归处理问题的思路流程: 加载数据:
def loadDataSet(fileName):
numFeat = len(open(fileName).readline().split(‘\t‘)) - 1 # 数据点特征的数量
dataMat = []
labelMat = []
fr = open(fileName)
for line in fr.readlines():
lineArr = []
curLine = line.strip().split(‘\t‘)
for i in range(numFeat):
lineArr.append(float(curLine[i]))
dataMat.append(lineArr)
labelMat.append(float(curLine[-1]))
return dataMat,labelMat
该函数返回两个值:数据点特征值矩阵dataMat,数据点目标值向量labelMat。 下面函数是标准线性回归函数,求解回归系数的过程:
def standRegres(xArr,yArr):
xMat = mat(xArr)
yMat = mat(yArr).T
xTx = xMat.T * xMat
if linalg.det(xTx) == 0: # 判断矩阵的行列式是否为0
print(‘This matrix is singular, cannot do inverse‘)
return
ws = xTx.I * (xMat.T * yMat) # ws为列向量,对应特征的个数
return ws
上面函数中计算回归系数用到了$w = {({X}^{T}X)}^{-1}{X}^{T}y$,接着打开数据文件并通过绘图看线性回归的结果:
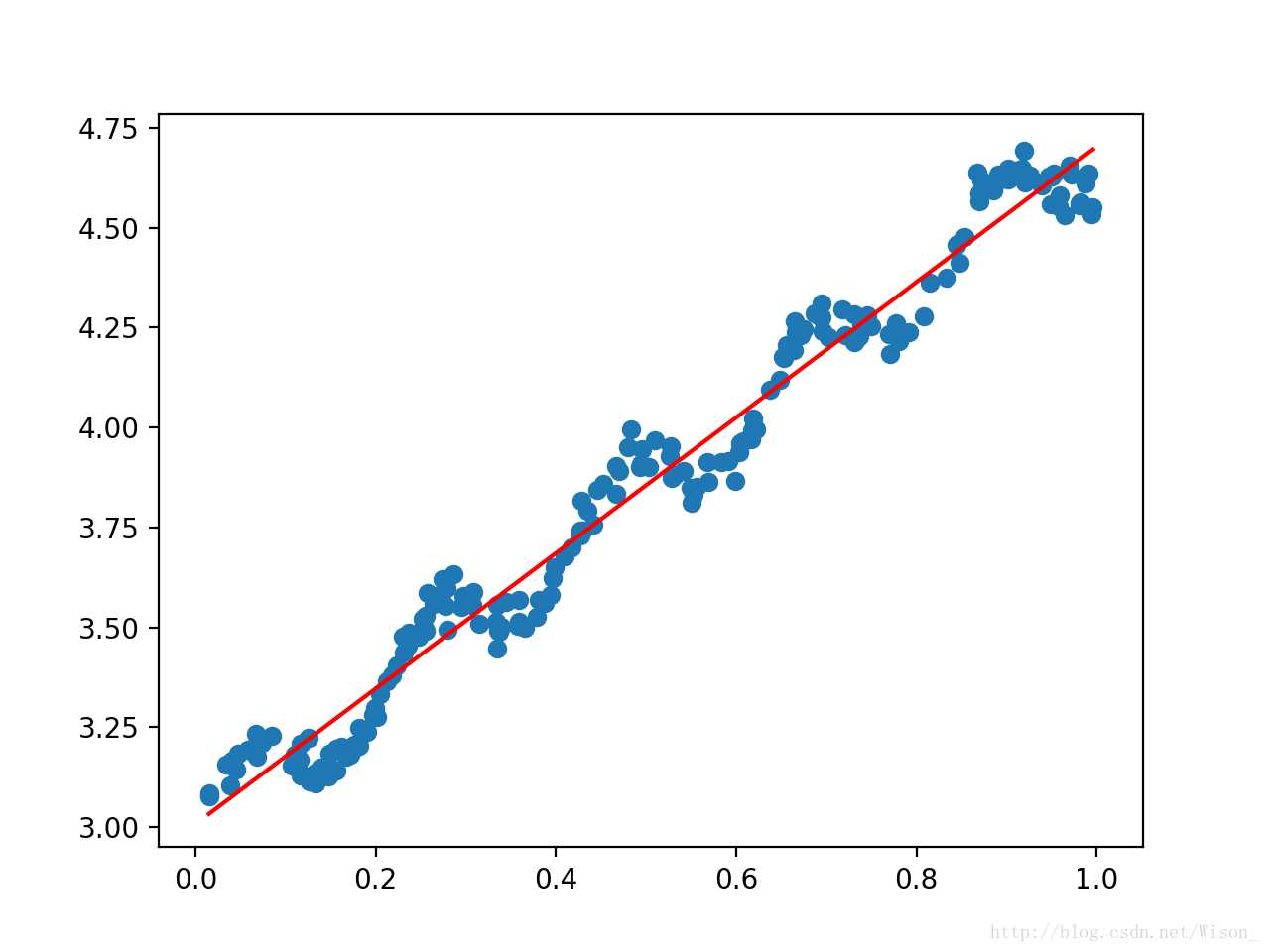
xArr,yArr = loadDataSet(‘/Users/Desktop/ex0.txt‘) ws = standRegres(xArr,yArr) xMat = mat(xArr) yMat = mat(yArr) yHat = xMat * ws #yHat为预测值 fig = plt.figure() ax = fig.add_subplot(111) ax.scatter(xMat[ : ,1].flatten().A[0], yMat.T[ : ,0].flatten().A[0]) xCopy = xMat.copy() xCopy.sort(0) yHat = xCopy * ws ax.plot(xCopy[ : ,1], yHat,color = ‘red‘) plt.show()
输出图形如下:蓝色部分为数据点,红色线为通过线性回归计算出回归系数后作出的直线。
线性回归的一个问题是有可能出现欠拟合现象,在对新数据进行预测的时候可能会有较大的偏差,因此这里接着介绍另一种方法:局部加权回归: 给待预测点附近的每个点赋予更高的权重,然后在这个子集上基于最小均方差来进行普通的回归,因此,这种方法每次预测均需要事先选取出对应的数据子集。 该算法回归系数的计算式为:$w = {({X}^{T}WX)}^{-1}{X}^{T}Wy$,其中W表示每个数据点权重值。 下面是局部加权回归函数代码,参数中k决定了对预测点附近的点赋予多大的权重,k值越小,预测点附近的点权重越大,该参数由用户指定,返回值为回归系数ws。
def lwlr(testPoint,xArr,yArr,k = 1.0):
xMat = mat(xArr)
yMat = mat(yArr).T
m = shape(xMat)[0] # 训练样本点数量
weights = mat(eye((m))) # 初始化权重 单位矩阵
for j in range(m):
diffMat = testPoint - xMat[j, : ]
weights[j,j] = exp(diffMat * diffMat.T / (-2 * k ** 2))
xTx = xMat.T *( weights * xMat)
if linalg.det(xTx) == 0:
print(‘This matrix is singular, cannot do inverse‘)
return
ws = xTx.I * (xMat.T * (weights * yMat))
return testPoint * ws
def lwlrTest(testArr, xArr, yArr, k = 1.0):
m = shape(testArr)[0] # 测试数据点的个数
yHat = zeros(m) # 创建点保存预测值
for i in range(m):
yHat[i] = lwlr(testArr[i],xArr,yArr,k)
return yHat
调用上面的函数,改变k的值,从上到下分别为1,0.01,0.003,输出结果分别如下所示:
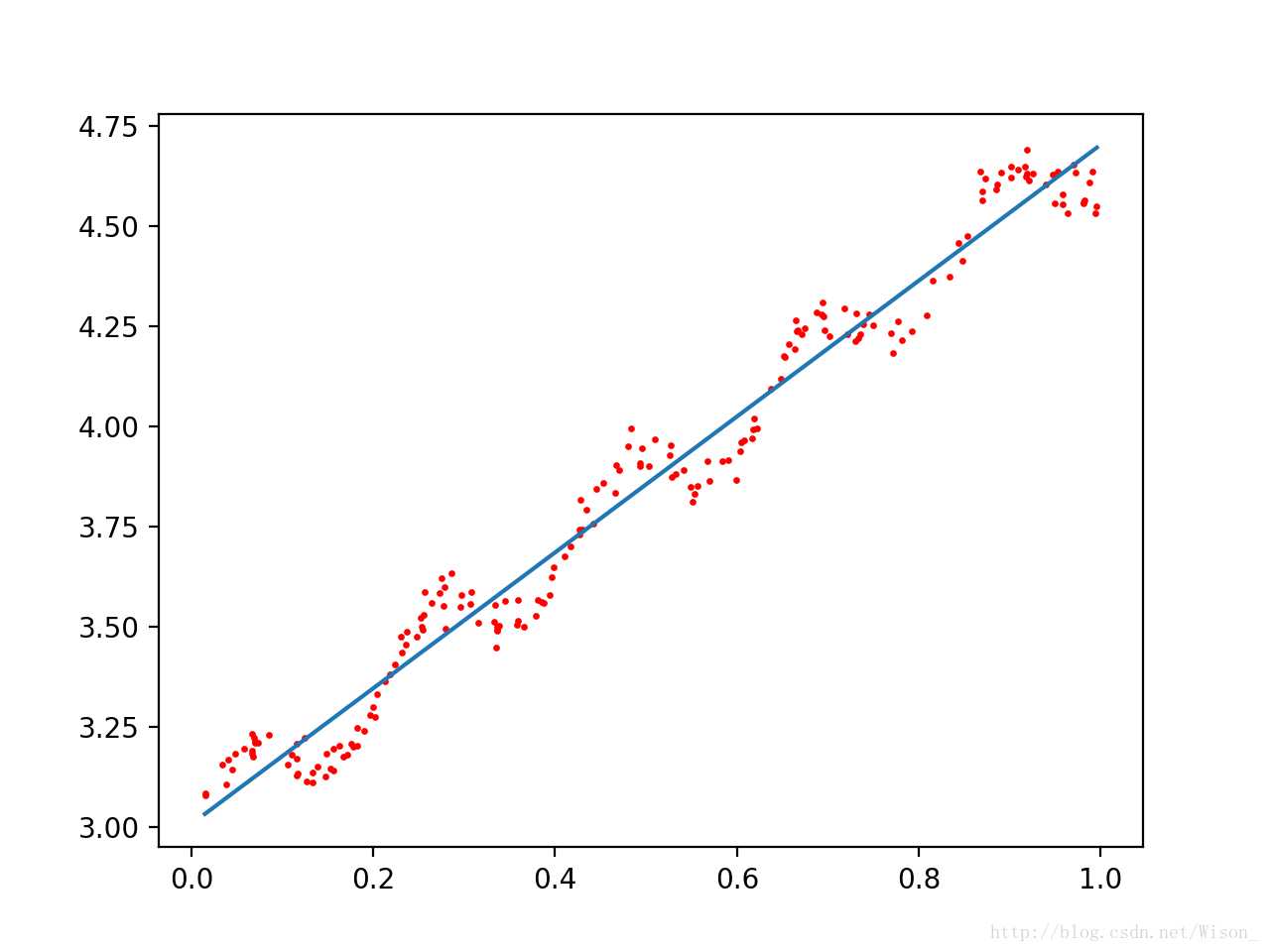
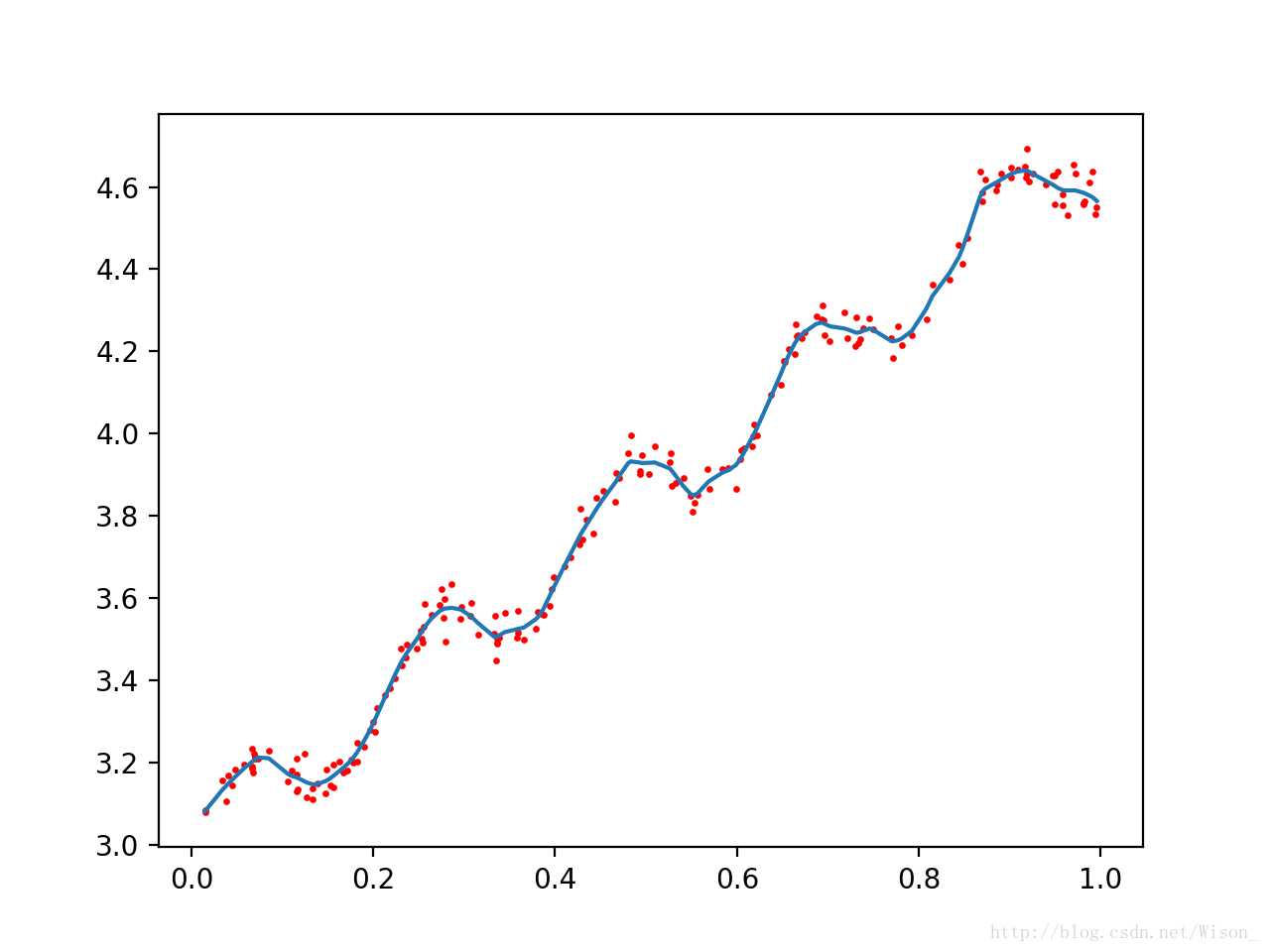
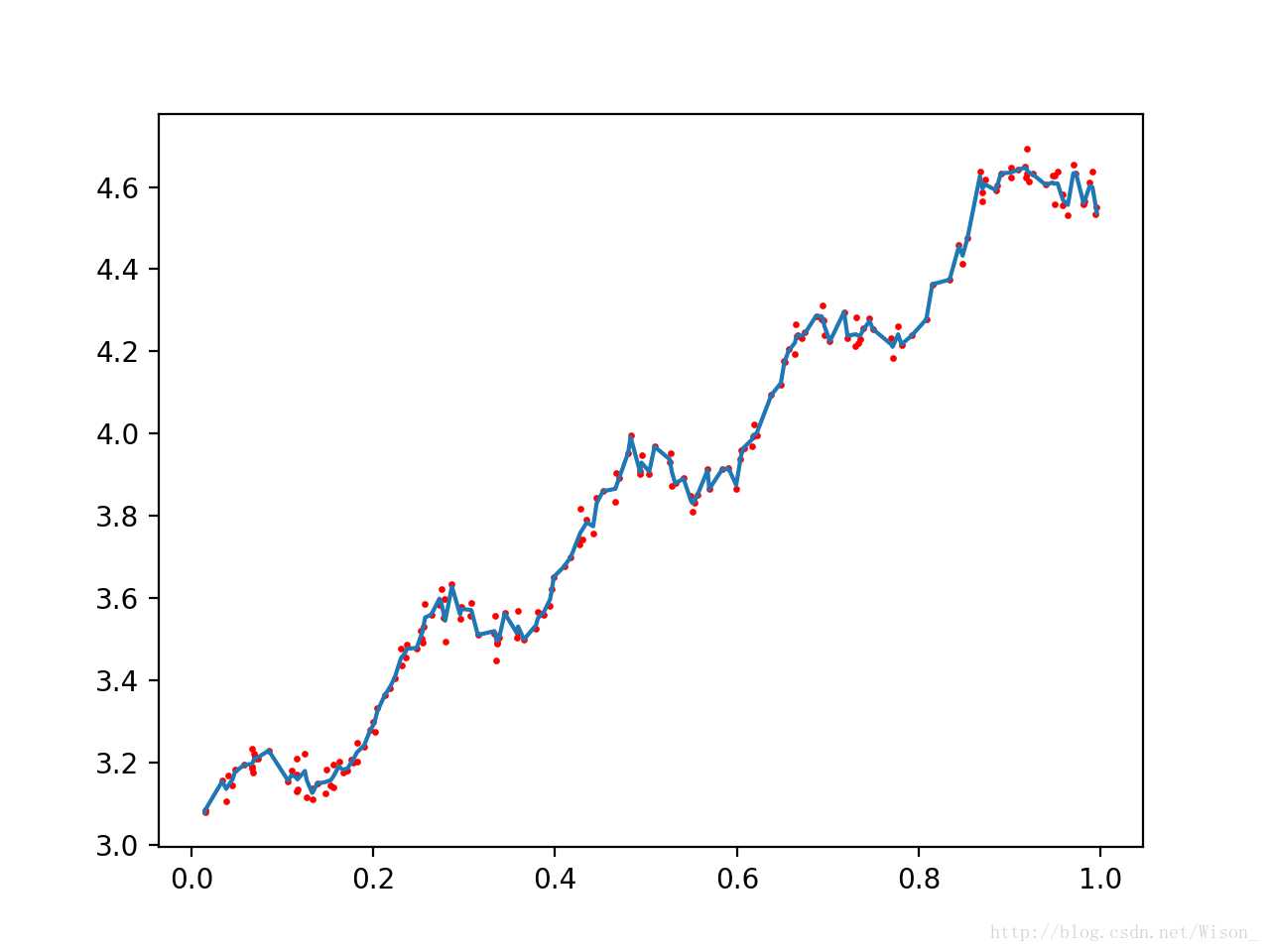
局部加权回归存在的问题是增加了计算量,因为对每个数据点进行预测时都必须使用整个数据集。上面的三种情况中,k = 0.01是能够较好的实现对数据点的预测的,而且当 k = 0.01时,大多数数据点(训练数据点)的权重都接近零。如果能避免这些计算将可以减少计算量和程序运行的时间。
标签:near plot 测试数据 通过 dataset 代码 数值 红色 curl
原文地址:http://www.cnblogs.com/weimusan/p/7499930.html