标签:auto == ubuntu using 命名 names a.out 语句 意图
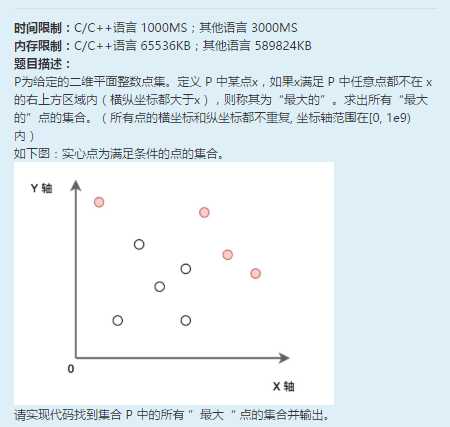
PS:这篇是之前本来就想发的但是一直没时间写,加上今天做了京东的题,结果代码名就命名为jingdong了……懒得改代码名重新跑一遍结果了=。=
暴力法去做就是遍历每个点,判断它是不是“最大点”。判断过程则是又遍历一遍,看看是否存在其他点在它右上方,若存在则不是最大点。O(N^2)
但是这样就会有很多不必要的计算,举个例子(这里暂且当坐标都是int),若存在一个最大点(x0,y0),那么所有在它左下角的点都不用考虑了。
另外,对于(x0,y0),只需要查找在它右边(x>x0)的点是否在它上面。如果预先将点根据x坐标排序,那么判断过程就从for i in [0, n)变成了for i in [x0, n),但这并没有本质的提升,还是O(N^2)。——这也暗示了点集中最右边的点必然是最大点。
然后再注意,如果右边的点存在一个点满足y>y0,那么判断就会返回false了;若不存在则判断返回true。
关键就是记录右边的点的ymax,不必每次都遍历一遍重复计算ymax。
到了这一步后就可以写代码了,注意,由于输入并不是有序的,必须得经过预处理(按照x排序),坐标轴范围是0~1e9的话,用位图法排序(参考编程珠玑)时间复杂度还是1e9的数量级,原题数据量不超过100000,位图法排序并不比快排快。
#include <algorithm> #include <limits.h> using namespace std; struct Point { int x, y; }; // a[n]为从输入中读取得到的点集数组 void solution(Point* a, int n) { std::sort(a, a + n, [](Point& p1, Point& p2) { return p1.x < p2.x; }); int ymax = INT_MIN; // 记录从右往左遍历过程中y的最大值 for (int i = n - 1; i >= 0; i--) { if (a[i].y > ymax) // 此时a[i].y大于或等于右边所有点的最大y坐标, a[i]为最大点 { printf("%d %d\n", a[i].x, a[i].y); ymax = a[i].y; // 更新最大y坐标 } } }
上述代码的成功有个前提,也是题目里的限制:【所有点的横纵坐标都不重复】
这点必须注意!如果没有这个限制,比如y坐标不重复,比如对点集(1,1) (2,3) (3,3) (4,2),按照上面的做法只会得出(3,3)和(4,2)两个最大点,但是(2,3)其实也是最大点。
错误的地方在于判断语句:a[i].y > ymax,如果该点的y坐标与ymax相等,那么该点也是最大点.。
因此判断语句要改成
if (a[i].y >= ymax)
如果连x坐标不重复这个限制都没有的话,那就更复杂,比如序列经过sort排序后为(1,3)(1,4)(2,2),(2,2)和(1,4)被确认为最大点,但是判断(1,3)时,由于当前ymax已经被更新为4了,(1,3)不会被当成最大点。
这样一来,逻辑就变成了【对所有满足x=x0的点,其中y>=ymax的点都是最大点】,关键是要找出满足x=x0的点集区间。
在没有【所有的横纵坐标都不重复】这个限制下的完整代码与简单测试结果如下
#include <iostream> #include <vector> #include <algorithm> #include <limits.h> using namespace std; struct Point { int x, y; Point(int x_, int y_) : x(x_), y(y_) { } bool operator<(const Point& rhs) const { return x < rhs.x; } }; void solution(Point* a, int n) { vector<Point> res; res.reserve(n); // 注释掉排序预处理的代码, 输入排序后的结果进行测试 // 因为快排不是稳定排序, 可能打乱x相同的若干点之间的相对顺序 // sort(a, a + n); int ymax = INT_MIN; // 记录从右往左遍历过程中y的最大值 Point* low = &a[n - 1]; Point* high = &a[n]; while (low >= a) { // 寻找x坐标相同的左闭右开区间 while (low > a) // 保证low-1在a[n]中 { auto it = low - 1; if (it->x == low->x) low = it; else break; } // 左闭右开区间[low, high)的点的x坐标相同 // 区间内所有y不小于ymax的点均为最大点 int temp = ymax; for (auto it = low; it != high; ++it) { if (it->y >= ymax) { res.emplace_back(*it); if (it->y > temp) // 同时求出[low, a+n)区间的最大y坐标 temp = it->y; } } ymax = temp; high = low; low = high - 1; } // 按照x坐标从小到大输出结果 std::sort(res.begin(), res.end()); for (auto& pt : res) cout << pt.x << " " << pt.y << endl; } int main() { // 读取输入 int n; // 点数 cin >> n; vector<Point> v; v.reserve(n); for (int i = 0; i < n; i++) { int x,y; cin >> x >> y; v.emplace_back(x, y); } // 计算并输出结果 solution(&v[0], v.size()); return 0; }
测试用例data1是针对特殊情况(x/y坐标有重复的)的用例,data2是题目的示意图的用例
xyz@ubuntu:~/Algorithms/2017$ g++ jingdong.cpp -std=c++11 xyz@ubuntu:~/Algorithms/2017$ cat data1 4 1 2 1 3 1 4 2 3 xyz@ubuntu:~/Algorithms/2017$ cat data1 | ./a.out 1 3 1 4 2 3 xyz@ubuntu:~/Algorithms/2017$ cat data2 9 1 10 2 3 3 8 4 4 5 6 5 3 6 9 7 7 8 5 xyz@ubuntu:~/Algorithms/2017$ cat data2 | ./a.out 1 10 6 9 7 7 8 5
如果是在题目限制下的算法,对data1的结果如下(漏掉了(1,3)这个点)
xyz@ubuntu:~/Algorithms/2017$ g++ jingdong_old.cpp -std=c++11 xyz@ubuntu:~/Algorithms/2017$ cat data1 | ./a.out 1 4 2 3
2017头条笔试题:二维点集中找出右上角没有点的点并按x坐标从小到大打印坐标
标签:auto == ubuntu using 命名 names a.out 语句 意图
原文地址:http://www.cnblogs.com/Harley-Quinn/p/7419183.html