标签:mat 一个 get 范围 noi typedef include c代码 ica
Problem 2 数列(seq.cpp/c/pas)
【题目描述】
a[1]=a[2]=a[3]=1
a[x]=a[x-3]+a[x-1] (x>3)
求a数列的第n项对1000000007(10^9+7)取余的值。
【输入格式】
第一行一个整数T,表示询问个数。
以下T行,每行一个正整数n。
【输出格式】
每行输出一个非负整数表示答案。
【样例输入】
3
6
8
10
【样例输出】
4
9
19
【数据范围】
对于30%的数据 n<=100;
对于60%的数据 n<=2*10^7;
对于100%的数据 T<=100,n<=2*10^9;
洛谷上也有https://www.luogu.org/problem/show?pid=1939
乍一看感觉是一道模拟题,但是巨大的数据范围让人望而生畏,一般期望得分为60分。
如何得到100分成为了一个难点。
经过分析,不难发现递推公式$a[x]=a[x-3]+a[x-1](x>3)$与Fibonacci数列十分相似,我们可以进行转化,得到这道题的做法,快速求Fibonacci数列。
至于快速求Fibonacci数列的方法主要是矩阵快速幂。
所以这道题就转化为了求矩阵快速幂,而矩阵快速幂的本质是矩阵乘法,至于什么是矩阵乘法,大家可以上网搜索一下,博主个人感觉这篇博客写得还不错。
矩阵乘法代码实现:
1 struct Matrix{ 2 ll a[3][3]; 3 }; 4 5 Matrix multiply(Matrix x, Matrix y) 6 { 7 Matrix t; 8 for(int i = 0; i < 3; i++) 9 for(int j = 0; j < 3; j++) 10 { 11 t.a[i][j] = 0; 12 for(int k = 0; k < 3; k++) 13 t.a[i][j] = (t.a[i][j] + x.a[i][k] * y.a[k][j] % MOD) % MOD; 14 } 15 return t; 16 }
如果只用矩阵乘法时间复杂度与模拟没有什么区别,甚至更甚,所以我们需要进行简化,因为矩阵相乘满足结合律,所以矩阵$A*A*A*A$可以写成$(A*A)*(A*A)$,也就是说几个相同的矩阵相乘本质就相当于几个数相乘,也就是说,矩阵$A*A*A*A$与$A^{4}$区别不大,我们就可以用快速幂来计算多个相同的矩阵相乘。至于快速幂的本质实际上是二分。
1 struct Matrix{ 2 ll a[3][3]; 3 }; 4 5 Matrix multiply(Matrix x, Matrix y) 6 { 7 Matrix t; 8 for(int i = 0; i < 3; i++) 9 for(int j = 0; j < 3; j++) 10 { 11 t.a[i][j] = 0; 12 for(int k = 0; k < 3; k++) 13 t.a[i][j] = (t.a[i][j] + x.a[i][k] * y.a[k][j] % MOD) % MOD; 14 } 15 return t; 16 } 17 18 Matrix pow_mod(Matrix a, ll p) 19 { 20 Matrix base = a; 21 Matrix res = a; 22 p--; 23 while(p) 24 { 25 if(p&1) res = multiply(res, base); 26 base = multiply(base, base); 27 p >>= 1; 28 } 29 return res; 30 }
那么到底怎么用矩阵快速幂来解决知道题呢?看图
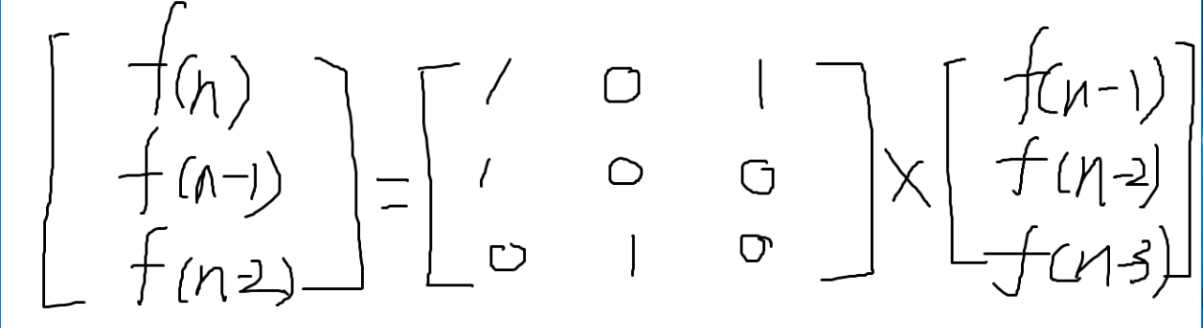
每做一次乘法就相当于递推一次,而我们需要递推N次,就相当在初始矩阵上反复乘
$1 0 1$
$1 0 0$
$0 1 0$
循环n次就是乘n次,这样就可以用矩阵快速幂了。
题目AC代码:
1 #include <cstdio> 2 #include <cstring> 3 #include <algorithm> 4 5 using namespace std; 6 7 typedef long long ll; 8 const int MOD = 1e9 + 7; 9 10 struct Matrix{ 11 ll a[3][3]; 12 }; 13 14 Matrix multiply(Matrix x, Matrix y) 15 { 16 Matrix t; 17 for(int i = 0; i < 3; i++) 18 for(int j = 0; j < 3; j++) 19 { 20 t.a[i][j] = 0; 21 for(int k = 0; k < 3; k++) 22 t.a[i][j] = (t.a[i][j] + x.a[i][k] * y.a[k][j] % MOD) % MOD; 23 } 24 return t; 25 } 26 27 Matrix pow_mod(Matrix a, ll p) 28 { 29 Matrix base = a; 30 Matrix res = a; 31 p--; 32 while(p) 33 { 34 if(p&1) res = multiply(res, base); 35 base = multiply(base, base); 36 p >>= 1; 37 } 38 return res; 39 } 40 41 int t; 42 int ans[110]; 43 Matrix m, x, y; 44 45 int main() 46 { 47 scanf("%d", &t); 48 m.a[0][0] = 1; m.a[0][1] = 0; m.a[0][2] = 1; 49 m.a[1][0] = 1; m.a[1][1] = 0; m.a[1][2] = 0; 50 m.a[2][0] = 0; m.a[2][1] = 1; m.a[2][2] = 0; 51 for(int i = 1; i <= t; i++) 52 { 53 int d; 54 scanf("%d", &d); 55 if(d <= 3) 56 { 57 printf("1\n"); 58 continue; 59 } 60 x=pow_mod(m, d - 3); 61 ll sum = 0; 62 for(int i = 0; i < 3; i++) 63 sum = (sum + x.a[0][i]) % MOD; 64 printf("%d\n", sum); 65 } 66 return 0; 67 }
标签:mat 一个 get 范围 noi typedef include c代码 ica
原文地址:http://www.cnblogs.com/Y-sofun/p/7500325.html