标签:one set test 关系 amp can 分类 scan size
Given a triangle field and a rope of a certain length (Figure-1), you are required to use the rope to enclose a region within the field and make the region as large as possible.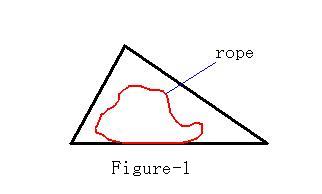
题意:给你一个三角形的三个边,再给你一条长度为len的绳子.让你用绳子在三角形内圈出来一个区域让这个区域面积最大
思路:
我可以分类思考这个问题
1.如果绳子比三角形的周长还要长的话,最大的面积显然是这个三角形的面积
2.如果绳子很短呢?显然围成一个圆的时候面积是最大的.三角形里面最大的圆就是它的内切圆了
也就是说如果绳子的长度比三角形内切圆的周长还要小的时候,让它围成一个圆
3.当绳子介于1 2 的长度之间的呢?
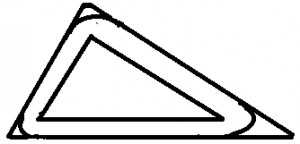
当自由线从内切圆那种情况继续膨胀到能与三角形的边贴近但长度小于三角形周长时,将这个已经围成的面积划分为三个部分:
能构成一个更小的内切圆的三段弧,以三段弧的中心连结起来的一个更小且与原三角形相似的三角形,与原三角形贴近的三条边
所围成的三个矩形面积.
1 #include <bits/stdc++.h> 2 3 using namespace std; 4 #define eps 1e-9 5 #define pi acos(-1.0) 6 #define zero(x) (((x)>0?(x):-(x))<eps) 7 double a,b,c,len; 8 int main() 9 { 10 //freopen("de.txt","r",stdin); 11 int casee = 0; 12 while (~scanf("%lf%lf%lf%lf",&a,&b,&c,&len)){ 13 //len为自由线的长度;p0为原三角形的周长;p1为原三角形的半周长; 14 //R为原三角形的内切圆半径;r为相似三角形的内切圆半径。 15 if (zero(a+b+c+len)) 16 break; 17 printf("Case %d: ",++casee); 18 double p0 = a+b+c; 19 double p1 = p0/2; 20 double S = sqrt(p1*(p1-a)*(p1-b)*(p1-c)); 21 double R = 2*S/p0;//三角形内切圆公式S=p0*R/2; R为内切圆半径 22 if (len>=p0) 23 { 24 printf("%.2f\n",S); 25 continue; 26 } 27 else if (2*pi*R-len>eps){ 28 R = len/pi/2; 29 S = pi*R*R; 30 printf("%.2f\n",S); 31 continue; 32 } 33 else{ 34 double r = (p0-len)/(p0/R-2*pi); 35 //利用的就是三角形相似的原理;公式;p0/R*(R-r)=len-2*pi*r;左边是通过内切圆半径与周长的关系求 36 //得小三角形的周长;右边是通过自由线的长度减掉三段弧得到相似三角形的周长; 37 double radio = (R-r)/R;//相似比 38 a*=radio; 39 b*=radio; 40 c*=radio; 41 double p=(a+b+c)/2; 42 S = pi*r*r+sqrt(p*(p-a)*(p-b)*(p-c))+r*2*p; 43 printf("%.2f\n",S); 44 continue; 45 46 } 47 } 48 return 0; 49 }
hdu 1451 Area in Triangle(计算几何 三角形)
标签:one set test 关系 amp can 分类 scan size
原文地址:http://www.cnblogs.com/agenthtb/p/7500627.html