标签:代码 树节点 9.png div http oid count 相等 顺序
一、基本概念
每个结点最多有两棵子树,左子树和右子树,次序不可以颠倒。
性质:
1、非空二叉树的第n层上至多有2^(n-1)个元素。
2、深度为h的二叉树至多有2^h-1个结点。
满二叉树:所有终端都在同一层次,且非终端结点的度数为2。
在满二叉树中若其深度为h,则其所包含的结点数必为2^h-1。
完全二叉树:除了最大的层次即成为一颗满二叉树且层次最大那层所有的结点均向左靠齐,即集中在左面的位置上,不能有空位置。
对于完全二叉树,设一个结点为i则其父节点为i/2,2i为左子节点,2i+1为右子节点。
二、存储结构
顺序存储:
将数据结构存在一块固定的数组中。
虽然在遍历速度上有一定的优势,但因所占空间比较大,是非主流二叉树。二叉树通常以链式存储。
链式存储:
包含二叉树链式结构,以及后面将会使用的栈和队列的结构
1 //二叉树 2 typedef struct object{ 3 struct object *p, *left, *right; 4 5 int key; 6 }object_s; 7 8 typedef struct binarytree{ 9 object_s *proot; 10 }binarytree_s; 11 12 //栈 13 typedef struct stack{ 14 object_s *data[STACK_SIZE]; 15 int tag[STACK_SIZE]; //为后序遍历准备的 16 int top; 17 }stack_s; 18 19 //队列 20 typedef struct queue{ 21 object_s *data[QUEUE_SIZE]; 22 int head,tail; 23 }queue_s;
三、二叉树的遍历
遍历即将树的所有结点访问且仅访问一次。按照根节点位置的不同分为前序遍历,中序遍历,后序遍历。
前序遍历:根节点->左子树->右子树
中序遍历:左子树->根节点->右子树
后序遍历:左子树->右子树->根节点
例如:求下面树的三种遍历
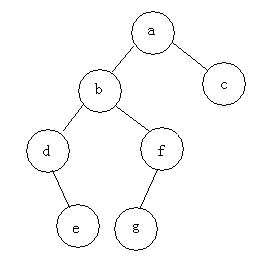
前序遍历:abdefgc
中序遍历:debgfac
后序遍历:edgfbca
其他的遍历方式:按照层次遍历
四、遍历方式的实现
利用前序遍历初始化二叉树
1 void createtree(object_s **ppt) 2 { 3 int i,ret; 4 ret = scanf("%d",&i); 5 if(ret == 0) 6 return; 7 8 if(i == -1) { 9 *ppt = NULL; 10 } else { 11 *ppt = (object_s*)malloc(sizeof(object_s)); 12 (*ppt)->key = i; 13 (*ppt)->p=NULL; 14 (*ppt)->left=NULL; 15 (*ppt)->right=NULL; 16 createtree(&((*ppt)->left)); 17 createtree(&((*ppt)->right)); 18 } 19 }
前序遍历-递归实现
1 void preorder(object_s *ptree) 2 { 3 if(ptree) { 4 printf("%d ", ptree->key); 5 preorder(ptree->left); 6 preorder(ptree->right); 7 } else { 8 return; 9 } 10 }
前序遍历-非递归实现
1 void preorder1(binarytree_s *ptree) 2 { 3 stack_s s; 4 object_s *pnode; 5 s.top=0; 6 7 if(ptree->proot == NULL) { 8 printf("the tree is empty\n"); 9 } else { 10 pnode = ptree->proot; 11 // 当前结点不为空 或 栈不为空 12 while(pnode!=NULL || s.top!=0) { 13 while(pnode != NULL) { 14 printf("%d ", pnode->key); 15 push(&s,pnode); 16 pnode = pnode->left; 17 } 18 pnode = pop(&s); 19 pnode = pnode->right; 20 } 21 } 22 }
中序遍历-递归实现
1 void midorder(object_s *ptree) 2 { 3 if(ptree) { 4 preorder(ptree->left); 5 printf("%d ", ptree->key); 6 preorder(ptree->right); 7 } else { 8 return; 9 } 10 }
中序遍历-非递归实现
1 void midorder1(binarytree_s *ptree) 2 { 3 stack_s s; 4 object_s *pnode; 5 s.top=0; 6 7 if(ptree->proot == NULL) { 8 printf("the tree is empty\n"); 9 } else { 10 pnode = ptree->proot; 11 // 当前结点不为空 或 栈不为空 12 while(pnode!=NULL || s.top!=0) { 13 while(pnode != NULL) { 14 push(&s,pnode); 15 pnode = pnode->left; 16 } 17 pnode = pop(&s); 18 printf("%d ",pnode->key); 19 pnode = pnode->right; 20 } 21 } 22 }
后续遍历-递归实现
1 void postorder(object_s *ptree) 2 { 3 if(ptree) { 4 preorder(ptree->left); 5 preorder(ptree->right); 6 printf("%d ", ptree->key); 7 } else { 8 return; 9 } 10 }
后序遍历-非递归实现
1 void postorder1(binarytree_s *ptree) 2 { 3 stack_s s; 4 object_s *pnode; 5 int tag; 6 s.top=0; 7 8 if(ptree->proot == NULL) { 9 printf("the tree is empty\n"); 10 } else { 11 pnode = ptree->proot; 12 while(pnode!=NULL || s.top!=0) { 13 //向左走到底 14 push_post(&s,pnode,0); 15 pnode=pnode->left; 16 if(pnode==NULL) { 17 while(s.top!=0) { // 处理pop出来的对象 18 pnode = pop_post(&s,&tag); 19 //printf("debug key[%d] tag[%d]\n",pnode->key, tag); 20 if(tag==1) { // 第一次pop 21 push_post(&s,pnode,tag); 22 pnode = pnode->right; 23 if(pnode == NULL) 24 continue; 25 else //跳出内层循环向左走 26 break; 27 } else { // 第二次pop 28 printf("%d ",pnode->key); 29 if(pnode==ptree->proot) 30 pnode=NULL; 31 } 32 } 33 } 34 } 35 } 36 }
层次遍历-每层从做到右遍历
1 void levelorder(binarytree_s *ptree) 2 { 3 object_s *pnode; 4 queue_s quq; 5 quq.head=quq.tail=0; 6 7 pnode = ptree->proot; 8 if(pnode==NULL) { 9 printf("this is an empty tree\n"); 10 exit(1); 11 } else { 12 insertqueue(pnode, &quq); 13 } 14 15 while((pnode=deletequeue(&quq))!=NULL) { 16 printf("%d ",pnode->key); 17 if(pnode->left!=NULL) { 18 insertqueue(pnode->left, &quq); 19 } 20 if(pnode->right!=NULL) { 21 insertqueue(pnode->right, &quq); 22 } 23 } 24 25 return; 26 }
五、二叉树其他操作
二叉树的查找,可以在之前遍历的基础上进行查找
1 object_s *searchtree(binarytree_s *ptree, int key) 2 { 3 stack_s s; 4 object_s *pnode; 5 s.top=0; 6 7 if(ptree->proot == NULL) { 8 printf("the tree is empty\n"); 9 } else { 10 pnode = ptree->proot; 11 // 当前结点不为空 或 栈不为空 12 while(pnode!=NULL || s.top!=0) { 13 while(pnode != NULL) { 14 if(pnode->key == key) 15 return pnode; 16 //printf("%d ", pnode->key); 17 push(&s,pnode); 18 pnode = pnode->left; 19 } 20 pnode = pop(&s); 21 pnode = pnode->right; 22 } 23 } 24 }
统计节点个数,通过遍历统计
1 int counttree(binarytree_s *ptree) 2 { 3 stack_s s; 4 object_s *pnode; 5 int count=0; 6 s.top=0; 7 8 if(ptree->proot == NULL) { 9 printf("the tree is empty\n"); 10 } else { 11 pnode = ptree->proot; 12 // 当前结点不为空 或 栈不为空 13 while(pnode!=NULL || s.top!=0) { 14 while(pnode != NULL) { 15 count++; 16 push(&s,pnode); 17 pnode = pnode->left; 18 } 19 pnode = pop(&s); 20 pnode = pnode->right; 21 } 22 } 23 return count; 24 }
比较两个树是否相等
1 int equaltree(object_s *pobj1,object_s *pobj2) 2 { 3 if(!pobj1&&!pobj2) { 4 return 1; 5 } 6 if(pobj1&&pobj2&&pobj1->key==pobj2->key) { 7 if(equaltree(pobj1->left,pobj2->left)) 8 if(equaltree(pobj1->left,pobj2->left)) 9 return 1; 10 } 11 return 0; 12 }
求二叉树深度
1 int gettreehigh(object_s *pobj) 2 { 3 int lhigh,rhigh; 4 5 if(pobj==NULL) 6 return 0; 7 lhigh = gettreehigh(pobj->left); 8 rhigh = gettreehigh(pobj->right); 9 10 return lhigh+rhigh+1; 11 }
六、测试
测试代码
1 int main(void) 2 { 3 binarytree_s btree; 4 binarytree_s btree1,btree2; 5 6 createtree(&(btree.proot)); 7 printf("create binary tree end\n"); 8 printf("递归前序遍历\n"); 9 preorder(btree.proot); 10 printf("\n"); 11 12 printf("迭代前序遍历\n"); 13 preorder1(&btree); 14 printf("\n"); 15 16 printf("递归中序遍历\n"); 17 midorder(btree.proot); 18 printf("\n"); 19 20 printf("迭代中序遍历\n"); 21 midorder1(&btree); 22 printf("\n"); 23 24 printf("递归后序遍历\n"); 25 postorder(btree.proot); 26 printf("\n"); 27 28 printf("迭代后序遍历\n"); 29 postorder1(&btree); 30 printf("\n"); 31 32 printf("层次遍历\n"); 33 levelorder(&btree); 34 printf("\n"); 35 36 printf("查找节点5\n"); 37 if(searchtree(&btree, 2)==NULL) 38 printf("未找到key为2的节点\n"); 39 else 40 printf("找到key为5的节点\n"); 41 42 printf("二叉树节点个数为[%d]\n",counttree(&btree)); 43 44 printf("数的高度为[%d]",gettreehigh(btree.proot)); 45 46 // 测试二叉树是否相等 47 createtree(&(btree1.proot)); 48 printf("create binary tree1 end\n"); 49 createtree(&(btree2.proot)); 50 printf("create binary tree2 end\n"); 51 52 if(equaltree(btree1.proot,btree2.proot)) 53 printf("二叉树相等\n"); 54 else 55 printf("二叉树不相等\n"); 56 57 return; 58 }
测试结果
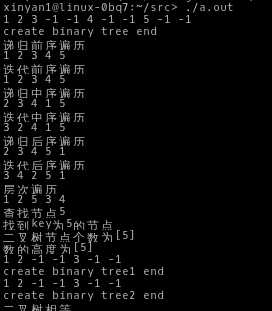
标签:代码 树节点 9.png div http oid count 相等 顺序
原文地址:http://www.cnblogs.com/yanxin880526/p/7500941.html