标签:否则 ide query tle sans math 技术 异或 png
[字典树专题]
这个星期学的东西不多,大体上就把字典树打熟了。字典树尽管NOIP不太会考,但是它的作用还是挺大的。
字典树也叫Trie树,是一种树形结构,一种哈希树的变种。下图就是一颗典型的trie(盗图者就是我):
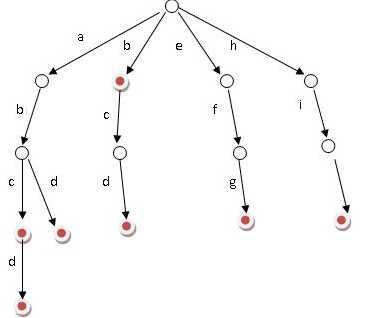
字典树有一些性质:
除了根节点没有字母编号,其他节点上面都有一个字母编号——即当前节点代表什么字母。
除了叶子节点没有子节点,其他节点都有一些子节点,这些子节点的字母编号都不同(一般是‘a’~‘z’中的某一些)。
从根节点出发,到某一个叶子节点,将经过节点的字母编号连起来就可以形成一个字符串,这个字符串是你插入的某一个单词(等下讲插入)。
我们设节点u有一些孩子,其中一个孩子是v,则ch[u][c]=v,其中c in [‘a‘..‘z‘](当然也可以是大写字母集合或01集合什么的)。
这表示编号为u,字母编号为c的子节点为编号为v的节点。
那么问题来了——字典树有什么用呢?
每错,Hash。可以合并某些冗余的空间(比如一颗前缀trie上,一些前缀相同的字符串拥有相同的前缀,省去了空间)。
首先,我们来说一下初始化。
主要是根节点的问题。我一般会把初始siz(大小)赋成1,表示根节点的编号。
code-init:
1 void init() {siz=0,memset(ch,0,sizeof ch);}
那么,我们来说一下这个插入(insert操作)。
假设你要insert一个字符串,那么——
从根节点出发,一步一步向下。
如果ch[u][s[i]-‘a‘]这个节点没有被用过,那么就开辟这个节点(并沿着新节点走),否则就沿着这个节点走下去。
code-insert:
1 void insert(char s[]) { 2 int u=1; 3 for (int i=0; i<strlen(s); i++) { 4 int c=s[i]-‘a‘; 5 if (!ch[u][c]) ch[u][c]=++siz; 6 u=ch[u][c]; 7 } 8 }
然后,假设我们要查询某字符串是否存在(相当于一个词典的作用),则
我们仍然像插入一样,从根节点下去,如果对应的子节点不存在,就false了。
code-query:
1 bool query(char s[]) { 2 int u=1; 3 for (int i=0; i<strlen(s); i++) { 4 int c=s[i]-‘a‘; 5 if (!ch[u][c]) return 0; 6 u=ch[u][c]; 7 } 8 return 1; 9 }
这是最简单的,最基础的关于字典树的操作。
有时候,会给字典树的每一个节点一个阈值,比如这是哪个字符串走下来的,或者有多少个字符串经过这个节点上面的,意义可以非常丰富。
尽管字典树名字叫做字典树,但是它的用处可绝不会仅仅局限于字符串。更多的反而在一些有xor并且数据很大的题目中应用。
比如HDU - 4825:
题目是中文的,意思很清楚。就是给你n个数,m个询问,m个询问每次给你一个数,要求n个数里面哪个数与给出的数异或值最大。
对于这一类题目,我们一般把不变的东西insert进01trie里面,然后进行操作。
对于每一个询问,要求出max(a[i]^z),这怎么办?由于异或没有特殊的性质,所以我们只好采取按位贪心处理。
幸好还有trie这种东西,我们不需要担心会TLE。
我们从31位处理到0位,如果在i位,设c=((1<<i)&z)>0,则表示z当前位为是0还是1,那么,根据贪心的想法,我们尽可能向ch[u][1-c]的方向走(异或尽可能大)。
如果存在ch[u][1-c]这个节点,那么就走下去,否则就往另一个方向走。
code:

1 #include<cstdio> 2 #include<cstring> 3 #include<algorithm> 4 #include<cmath> 5 #define LL long long 6 using namespace std; 7 const int maxnode=4000005; 8 int n,m; 9 LL a[maxnode]; 10 struct Trie{ 11 int ch[maxnode][2],va[maxnode],siz; 12 void init(){siz=0,memset(ch,255,sizeof ch),memset(va,0,sizeof va);} 13 void insert(LL x,int v){ 14 int u=0; 15 for (int i=31; i>=0; i--){ 16 bool c=(1ll<<i)&x; 17 if (ch[u][c]<0) ch[u][c]=++siz; 18 u=ch[u][c],va[u]=v; 19 } 20 } 21 int query(LL x){ 22 int u=0; 23 for (int i=31; i>=0; i--){ 24 bool c=(1ll<<i)&x; c=1-c; 25 if (ch[u][c]<0) u=ch[u][1-c]; 26 else u=ch[u][c]; 27 } 28 return va[u]; 29 } 30 }t; 31 inline LL read(){ 32 LL x=0; char ch=getchar(); 33 while (ch<‘0‘||ch>‘9‘) ch=getchar(); 34 while (ch>=‘0‘&&ch<=‘9‘) x=x*10+ch-‘0‘,ch=getchar(); 35 return x; 36 } 37 int main(){ 38 for (int T=read(),ts=1; ts<=T; ts++){ 39 n=read(),m=read(),t.init(); 40 for (int i=1; i<=n; i++) 41 a[i]=read(),t.insert(a[i],i); 42 printf("Case #%d:\n",ts); 43 for (int i=1; i<=m; i++){ 44 LL x=read(),idx=t.query(x); 45 printf("%lld\n",a[idx]); 46 } 47 } 48 return 0; 49 }
(ps:我写这份代码时还没改过来,大家尽量将siz的初值赋为1吧)
再来一题HYSBZ - 4260:
题意就是给你一个数组a,求出max(a[l1]^a[l1+1]^...^a[r1]+a[l2]^a[l2+1]^...^a[r2])(r1<l2)
由于xor的特殊性质,一个数异或两次相当于没有异或,所以
a[l]^a[l+1]^...^a[r]=a[1]^a[2]^...^a[l-1]^a[1]^a[2]^...^a[r-1]
那么,我们可以构造前缀异或和,然后insert进字典树里面。
然后搞一个前缀,f[i]表示r1<=i时,a[l1]^a[l1+1]^...^a[r1]的最大值,for i=1 to n,对于每一个i,将前缀异或和s作为上题的z一样操作,找一个异或最大的,则f[i]=max(f[i-1],query(s))。
接着是个后缀,g[i],做法一样。
最后扫一下,找出max(f[i]+g[i+1])就行了。
code:

1 #include<cstdio> 2 #include<cstring> 3 #include<algorithm> 4 #define jug(i,x) (((1<<i)&x)>0) 5 using namespace std; 6 const int N=400005; 7 int n,m,a[N],L[N],R[N],ans; 8 struct Trie{ 9 int ch[N*31][2],siz; 10 void init(){siz=1,memset(ch,0,sizeof ch);} 11 void insert(int x){ 12 int u=1; 13 for (int i=30; i>=0; i--){ 14 bool c=jug(i,x); 15 if (!ch[u][c]) ch[u][c]=++siz; 16 u=ch[u][c]; 17 } 18 } 19 int query(int x){ 20 int u=1,ret=0; 21 for (int i=30; i>=0; i--){ 22 bool c=jug(i,x); c=1-c; 23 if (ch[u][c]) u=ch[u][c],ret+=1<<i; 24 else u=ch[u][1-c]; 25 } 26 return ret; 27 } 28 }pre,suf; 29 inline int read(){ 30 int x=0; char ch=getchar(); 31 while (ch<‘0‘||ch>‘9‘) ch=getchar(); 32 while (ch>=‘0‘&&ch<=‘9‘) x=x*10+ch-‘0‘,ch=getchar(); 33 return x; 34 } 35 int main(){ 36 n=read(),pre.init(),suf.init(); 37 memset(L,0,sizeof L),memset(R,0,sizeof R); 38 pre.insert(0),suf.insert(0); 39 for (int i=1; i<=n; i++) a[i]=read(); 40 for (int i=1,s=0; i<=n; i++) 41 pre.insert(s^=a[i]), 42 L[i]=max(L[i-1],pre.query(s)); 43 for (int i=n,s=0; i>=1; i--) 44 suf.insert(s^=a[i]),R[i]=max(R[i+1],suf.query(s)); 45 ans=0; 46 for (int i=0; i<=n; i++) ans=max(ans,L[i]+R[i+1]); 47 printf("%d",ans); 48 return 0; 49 }
下一题也很水,HDU - 1251:
就是单纯的建立前缀trie。
code:

1 %:pragma gcc optimize(2) 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 using namespace std; 6 const int N=500005; 7 int n,Q,tot,ans; 8 struct Persistent_Trie{ 9 int sz,va[N],ch[N][26]; 10 void init() { 11 sz=1,memset(ch,0,sizeof ch); 12 memset(va,0,sizeof va); 13 } 14 void insert(char s[]) { 15 int len=strlen(s),u=1; 16 for (int i=0; i<len; i++){ 17 int c=s[i]-‘a‘; 18 if (!ch[u][c]) ch[u][c]=++sz; 19 u=ch[u][c],va[u]++; 20 } 21 } 22 int query(char s[]) { 23 int len=strlen(s),u=1; 24 for (int i=0; i<len; i++){ 25 int c=s[i]-‘a‘; 26 if (ch[u][c]) u=ch[u][c]; 27 else return 0; 28 } 29 return va[u]; 30 } 31 }pt; 32 inline int read() { 33 int x=0; char ch=getchar(); 34 while (ch<‘0‘||ch>‘9‘) ch=getchar(); 35 while (ch>=‘0‘&&ch<=‘9‘) x=x*10+ch-‘0‘,ch=getchar(); 36 return x; 37 } 38 int main() { 39 char s[20]; pt.init(); 40 for (; ;){ 41 gets(s); 42 if (s[0]<‘a‘||s[0]>‘z‘) break; 43 pt.insert(s); 44 memset(s,0,sizeof s); 45 } 46 while (scanf("%s",s)!=EOF) 47 printf("%d\n",pt.query(s)); 48 return 0; 49 }
还有部分较难的题目将会放在单独的题解里面。
加油↖(^ω^)↗
标签:否则 ide query tle sans math 技术 异或 png
原文地址:http://www.cnblogs.com/whc200305/p/7501613.html