1060: [ZJOI2007]时态同步

2017-09-10

Description

　　小Q在电子工艺实习课上学习焊接电路板。一块电路板由若干个元件组成，我们不妨称之为节点，并将其用数字1,2,3….进行标号。电路板的各个节点由若干不相交的导线相连接，且对于电路板的任何两个节点，都存在且仅存在一条通路（通路指连接两个元件的导线序列）。在电路板上存在一个特殊的元件称为“激发器”。当激发器工作后，产生一个激励电流，通过导线传向每一个它所连接的节点。而中间节点接收到激励电流后，得到信息，并将该激励电流传向与它连接并且尚未接收到激励电流的节点。最终，激烈电流将到达一些“终止节点”——接收激励电流之后不再转发的节点。激励电流在导线上的传播是需要花费时间的，对于每条边e，激励电流通过它需要的时间为te，而节点接收到激励电流后的转发可以认为是在瞬间完成的。现在这块电路板要求每一个“终止节点”同时得到激励电路——即保持时态同步。由于当前的构造并不符合时态同步的要求，故需要通过改变连接线的构造。目前小Q有一个道具，使用一次该道具，可以使得激励电流通过某条连接导线的时间增加一个单位。请问小Q最少使用多少次道具才可使得所有的“终止节点”时态同步？

Input

　　第一行包含一个正整数N，表示电路板中节点的个数。第二行包含一个整数S，为该电路板的激发器的编号。接下来N-1行，每行三个整数a , b , t。表示该条导线连接节点a与节点b，且激励电流通过这条导线需要t个单位时间

Output

　　仅包含一个整数V，为小Q最少使用的道具次数

Sample Input

3
1
1 2 1
1 3 3

Sample Output

N ≤ 500000，te ≤ 1000000

看到这个题,首先脑补了一个树,因为是无根树,所以可以随便改变树的形状....那么我们可以以要求的点作为根...

那我们考虑怎么使ans最小.那么我们画图可以知道.

技术分享

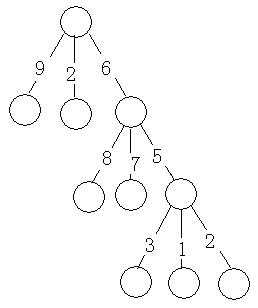
现在我们要使所有的最下面的点到根的距离都为相同,

那要使最下面3个点到根距离相同,就要让这层到他父节点的权值相同,即1->3;2->3就能使它合法

因为上层修改比下层修改要优,所以优先该上层,改每一层以最大的边权取max作为目标,贪心即可解决问题....

第一遍dfs找max,第二遍贪心选最小.ans即修改次数....

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<algorithm>
#define ll long long 
using namespace std;
const int maxn=500000+999;
int read(){
    int an=0,f=1;
    char ch=getchar();
    while(!(‘0‘<=ch&&ch<=‘9‘)){if(ch==‘-‘)f=-1;ch=getchar();}
    while(‘0‘<=ch&&ch<=‘9‘){an=an*10+ch-‘0‘;ch=getchar();}
    return an*f;
}
int n,Start,cnt,f[maxn],fa[maxn];
ll ma[maxn];
ll ans;
bool vis[maxn],vis2[maxn];
struct saber{
int nex,to,wi;
}b[maxn<<1];
void add(int x,int y,int z){
    cnt++;
    b[cnt].nex=f[x];
    f[x]=cnt;b[cnt].wi=z;
    b[cnt].to=y;
}
void dfs(int x){
    vis[x]=1;
    for(int i=f[x];i;i=b[i].nex){
        int v=b[i].to,wi=b[i].wi;
        if(!vis[v]){
            dfs(v);
            fa[v]=x;
            ma[x]=max(ma[x],ma[v]+wi);
        }
    }
}
void dfs2(int x){
    vis2[x]=1;
    for(int i=f[x];i;i=b[i].nex){
        int v=b[i].to,wi=b[i].wi;
        if(!vis2[v]){
        dfs2(v);
        ans+=(ma[x]-ma[v]-wi);
        }
    }
}
int main(){
    n=read();Start=read();
    for(int i=1;i<n;i++){
        int x=read(),y=read(),z=read();
        add(x,y,z);add(y,x,z);
    }
    dfs(Start);
    dfs2(Start);
    printf("%lld",ans);
    return 0;
}

时态同步

by:s_a_b_e_r

由s酱的理论可得，所有的DP都是贪心，于是这道题就是一道树上贪心x

考虑叶子节点，想让父节点到达所有叶子节点的时间相等，做法是取连接几个叶子节点的边权值的max值，然后把其他边都补到max

然后在处理这部分之上的父节点的时候，不管加哪条边都不会改变这几个叶子节点的同时性（自己起的名词qwq

所以就第一遍dfs求出所有节点到叶子节点路径权值的max，第二遍dfs统计答案f[i]

要统计的部分包括子节点的修改次数和对于这一层新添加的修改次数

最后，记得开long long

#include<iostream>
#include<cstdio>
#define ll long long
using namespace std;
const int N=500009;
int n,s,p[N],cnt,fa[N],ma[N];
ll f[N];
bool vis[N];
struct edge{
int to,nex;
int val;
}e[N<<1];
void add(int u,int v,int w)
{
     e[++cnt]=(edge){v,p[u],w};
     p[u]=cnt;
}
void dfs(int u)
{
     vis[u]=1;
     for(int i=p[u];i;i=e[i].nex)
     {
       int v=e[i].to;
       if(vis[v]){fa[u]=v;continue;}
       dfs(v);
       ma[u]=max(ma[u],ma[v]+e[i].val);
     }
}
void dfs2(int u)
{
     for(int i=p[u];i;i=e[i].nex)
     {
       int v=e[i].to;
       if(v==fa[u])continue;
       dfs2(v);
       f[u]+=f[v]+ma[u]-ma[v]-e[i].val;
     }
}
int main()
{
    scanf("%d%d",&n,&s);
    for(int i=1;i<n;++i)
    {
      int u,v,w;
      scanf("%d%d%d",&u,&v,&w);
      add(u,v,w);add(v,u,w);
    }
    dfs(s);
    dfs2(s);
    cout<<f[s]<<endl;
    return 0;
}

bzoj 1060

by:wypx

w:上边那个图是我后来改的

为什么一定要改呢？

因为s酱画的原图长这样↓

技术分享

s:我什么时候说所有的dp是贪心了poix

[ZJOI2007]时态同步

标签：解决 span 完成分享最小时间父节点 display zjoi

原文地址：http://www.cnblogs.com/ck666/p/7501922.html