标签:return clu tps scan 小数 lib 限制 col 一个
能评测了哦。
我们知道一棵有根树可以进行深度优先遍历(DFS)以及广度优先遍历(BFS)来生成这棵树的DFS序以及BFS序。两棵不同的树的DFS序有可能相同,并且它们的BFS序也有可能相同,例如下面两棵树的DFS序都是1 2 4 5 3,BFS序都是1 2 3 4 5
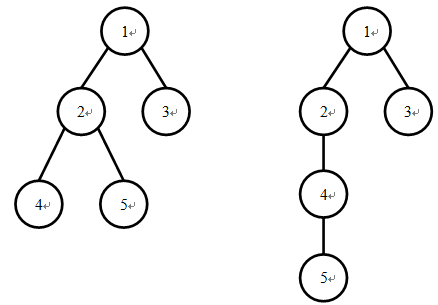
现给定一个DFS序和BFS序,我们想要知道,符合条件的有根树中,树的高度的平均值。即,假如共有K棵不同的有根树具有这组DFS序和BFS序,且他们的高度分别是h1,h2,...,hk,那么请你输出
(h1+h2..+hk)/k
输入格式:
输入文件count.in共有3行。
第一行包含1个正整数n,表示树的节点个数。
第二行包含n个正整数,是一个1~n的排列,表示树的DFS序。
第三行包含n个正整数,是一个1~n的排列,表示树的BFS序。
输入保证至少存在一棵树符合给定的两个序列。
输出格式:
输出文件count.out仅包含1个实数,四舍五入保留恰好三位小数,表示树高的平均值。
5 1 2 4 5 3 1 2 3 4 5
3.500
【评分方式】
如果输出文件的答案与标准输出的差不超过0.001,则将获得该测试点上的分数,否则不得分。
【数据规模和约定】
20%的测试数据,满足:n≤10;
40%的测试数据,满足:n≤100;
85%的测试数据,满足:n≤2000;
100%的测试数据,满足:2≤n≤200000。
【说明】
树的高度:一棵有根树如果只包含一个根节点,那么它的高度为1。否则,它的高度为根节点的所有子树的高度的最大值加1。
对于树中任意的三个节点a , b , c ,如果a, b都是c的儿子,则a, b在BFS序中和DFS序中的相对前后位置是一致的,即要么a都在b的前方,要么a都在b的后方。
【时间限制】
1s 【空间限制】
256000KB
这是一道思维好题.
为了方便考虑,先安装bfs序重新编号,这样bfn[i]=i.
若两个点之间必须分层,那么对答案的贡献就是1,可分可不分对答案的贡献为0.5.
先从bfs序考虑.
若dfn[i]<dfn[i-1]这时i和i-1必须分层.
再考虑dfs序中的相邻的两个点,x,y且bfn[x]<bfn[y].
这时x和y就最多分一层,就是要么y是x的儿子,要么y是x的右边的兄弟.
那么在bfn[x]-bfn[y]之间就最多分一层.
设s[i]代表i与i-1之间是否分层.
这样就会有一些不等关系.
那么先把必须分层记录一下,然后在不等关系里面判断一下是否分了,若已经分了的话,那么就把这一段区间标记为强制不分层.
最后那些没有标记的点对答案的贡献为0.5
1 #include<bits/stdc++.h> 2 #define maxn 200010 3 using namespace std; 4 int pos[maxn],dfn[maxn],s[maxn],c[maxn]; 5 double ans=1.0; 6 int main(){ 7 int n,x; 8 scanf("%d",&n); 9 for(int i=1;i<=n;i++) 10 scanf("%d",&dfn[i]),pos[dfn[i]]=i; 11 for(int i=1;i<=n;i++) 12 scanf("%d",&x),dfn[pos[x]]=i; 13 for(int i=1;i<=n;i++) pos[dfn[i]]=i; 14 s[2]=1; 15 for(int i=3;i<=n;i++) 16 if(pos[i]<pos[i-1])s[i]++,ans+=1.0; 17 for(int i=2;i<=n;i++) s[i]+=s[i-1]; 18 for(int i=3;i<=n;i++) 19 if(dfn[i-1]<dfn[i] && s[dfn[i]]-s[dfn[i-1]]) 20 c[dfn[i-1]+1]++,c[dfn[i]+1]--; 21 for(int i=3;i<=n;i++){ 22 c[i]+=c[i-1]; 23 if(!c[i]) ans+=0.5; 24 } 25 printf("%.3lf",ans+1.0); 26 return 0; 27 }
标签:return clu tps scan 小数 lib 限制 col 一个
原文地址:http://www.cnblogs.com/pantakill/p/7502741.html