标签:超过 空格 define odi 方案 答案 open amp --
丽江河边有n 家很有特色的客栈,客栈按照其位置顺序从 1 到n 编号。每家客栈都按照某一种色调进行装饰(总共 k 种,用整数 0 ~ k-1 表示),且每家客栈都设有一家咖啡店,每家咖啡店均有各自的最低消费。
两位游客一起去丽江旅游,他们喜欢相同的色调,又想尝试两个不同的客栈,因此决定分别住在色调相同的两家客栈中。晚上,他们打算选择一家咖啡店喝咖啡,要求咖啡店位于两人住的两家客栈之间(包括他们住的客栈),且咖啡店的最低消费不超过 p 。
他们想知道总共有多少种选择住宿的方案,保证晚上可以找到一家最低消费不超过 p元的咖啡店小聚。
输入文件hotel.in,共n+1 行。
第一行三个整数n ,k ,p,每两个整数之间用一个空格隔开,分别表示客栈的个数,色调的数目和能接受的最低消费的最高值;
接下来的n 行,第 i+1 行两个整数,之间用一个空格隔开,分别表示 i 号客栈的装饰色调和i 号客栈的咖啡店的最低消费。
输出格式:输出文件名为hotel.out 。
输出只有一行,一个整数,表示可选的住宿方案的总数。
5 2 3 0 5 1 3 0 2 1 4 1 5
3
【输入输出样例说明】
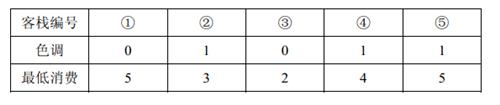
2 人要住同样色调的客栈,所有可选的住宿方案包括:住客栈①③,②④,②⑤,④⑤,但是若选择住4 、5 号客栈的话,4 、5 号客栈之间的咖啡店的最低消费是4 ,而两人能承受的最低消费是3 元,所以不满足要求。因此只有前 3 种方案可选。
【数据范围】
对于30% 的数据,有 n ≤100;
对于50% 的数据,有 n ≤1,000;
对于100%的数据,有 2 ≤n ≤200,000,0<k ≤50,0≤p ≤100 , 0 ≤最低消费≤100。
【题解】
这里有一枚比较好想的nlogn算法
这类问题首先想到“尺取法”,即固定左端点,枚举右端点,左右端点的某些属性满足单调性,从而做到On统计区间个数
枚举左端点l,令now为离l最近的、最低消费<=p的客栈位置,答案每次累加[now,r]的相同颜色的后缀和即可,注意now
与l相等时,累加值-1
后缀和用树状数组统计即可,直接统计10000000,可能会超时?

1 #include <iostream> 2 #include <cstdio> 3 #include <cstring> 4 #include <cstdlib> 5 #define lowbit(a) ((a) & (-a)) 6 7 inline void read(long long &x) 8 { 9 x = 0;char ch = getchar(), c = ch; 10 while(ch < ‘0‘ || ch > ‘9‘)c = ch, ch = getchar(); 11 while(ch <= ‘9‘ && ch >= ‘0‘)x = x * 10 + ch - ‘0‘, ch = getchar(); 12 if(c == ‘-‘)x = -x; 13 } 14 15 const long long MAXN = 200000 + 100; 16 const long long MAXK = 50 + 5; 17 18 long long n,k,p,mi[MAXN],color[MAXN],fee[MAXN]; 19 20 long long data[MAXK][MAXN]; 21 22 inline void modify(long long co, long long place, long long num) 23 { 24 for(;place <= n;place += lowbit(place)) 25 data[co][place] += num; 26 } 27 28 inline long long ask(long long co, long long place) 29 { 30 long long sum = 0; 31 for(;place;place -= lowbit(place)) 32 sum += data[co][place]; 33 return sum; 34 } 35 36 long long ans; 37 38 int main() 39 { 40 read(n), read(k), read(p); 41 for(register long long i = 1;i <= n;++ i) 42 { 43 read(color[i]), read(fee[i]); 44 ++ color[i]; 45 modify(color[i], i, 1); 46 } 47 for(register long long i = 1, j = 1;i <= n;++ i) 48 { 49 if(j < i)++ j; 50 while(fee[j] > p)++ j; 51 ans += ask(color[i], n) - ask(color[i], j - 1); 52 if(i == j)-- ans; 53 } 54 printf("%lld", ans); 55 return 0; 56 }
洛谷P1311 [NOIP2011提高组Day1T2] 选择客栈
标签:超过 空格 define odi 方案 答案 open amp --
原文地址:http://www.cnblogs.com/huibixiaoxing/p/7508235.html