标签:池化 truncate 图像 nta drop 利用 完成 否则 方式
卷积神经网络的概念最早出自19世纪60年代科学技术提出的感受野。当时科学家通过对猫的视觉皮层细胞研究发现,每一个视觉神经元只会处理一小块区域的视觉图像,即感受野。
一个卷积层中可以有多个不同的卷积核,而每一个卷积核都对应一个滤波后映射出的新图像,同一个新图像中每一个像素都来自完全相同的卷积核,这就是卷积核的权值共享。
权值共享是为了降低模型复杂度,减轻过拟合并降低计算量。
一个隐含节点对应于新产生的图的一个像素点
1994年LeNet (Yann LeCun)
1.首先载入MNIST数据集,并创建默认的Session
from tensorflow.examples.tutorials.mnist import input_data import tensorflow as tf mnist = input_data.read_data_sets("MNIST_data/",one_hot=True) sess = tf.InteractiveSession()
2. 定义常用函数,对于权重要制造一些随机的噪声来打破完全对称,比如截断的正态分布噪声,标准差设为0.1
对偏置也增加一些小的正值(0.1)来避免死亡节点(dead neurons)
对于conv2d函数,W是卷积核,shape=[5,5,1,32],表示卷积核大小为5x5,channel为1,共有32个
strides代表卷积模板移动的步长,因为都是二维平面移动,所以一般第一维和第四维固定为1,中间两维表示平面两个方向的步长[1,1,1,1]
padding表示边界的处理方式,这里SAME代表给边界加上padding让卷积的输出和输入保持同样的尺寸
pooling中的ksize表示窗口的大小,通常第一,第四维固定为1,中间两维表示平面窗口的大小
def weight_variable(shape): initial = tf.truncated_normal(shape,stddev=0.1) return tf.Variable(initial) def bias_variable(shape): initial = tf.constant(0.1,shape=shape) return tf.Variable(initial) def conv2d(x,W): return tf.nn.conv2d(x,W,strides=[1,1,1,1],padding=‘SAME‘) def max_pool_2x2(x): return tf.nn.max_pool(x,ksize=[1,2,2,1],strides=[1,2,2,1],padding=‘SAME‘)
3. 定义网络结构
注意输入是要reshape成平面结构用于卷积网络
所以若输入为[None,784],要将其转换成28x28的形状用作卷积 -1表示通过原尺寸自动计算该维的值,比如说 x = [4,7] x‘ = tf.reshape(x,[-1,14]) 那么 x‘ = [2,14]
x = tf.placeholder(tf.float32,[None,784]) y_ = tf.placeholder(tf.float32,[None,10]) x_image = tf.reshape(x,[-1,28,28,1]) W_conv1 = weight_variable([5,5,1,32]) b_conv1 = bias_variable([32]) h_conv1 = tf.nn.relu(conv2d(x_image,W_conv1)+b_conv1) h_pool1 = max_pool_2x2(h_conv1) W_conv2 = weight_variable([5,5,32,64]) b_conv2 = bias_variable([64]) h_conv2 = tf.nn.relu(conv2d(h_pool1,W_conv2)+b_conv2) h_pool2 = max_pool_2x2(h_conv2) W_fc1 = weight_variable([7*7*64,1024]) b_fc1 = bias_variable([1024]) h_pool2_flat = tf.reshape(h_pool2,[-1,7*7*64]) h_fc1 = tf.nn.relu(tf.matmul(h_pool2_flat,W_fc1)+b_fc1) keep_prob = tf.placeholder(tf.float32) h_fc1_drop = tf.nn.dropout(h_fc1,keep_prob) W_fc2= weight_variable([1024,10]) b_fc2 = bias_variable([10]) y_conv =tf.nn.softmax(tf.matmul(h_fc1_drop,W_fc2)+b_fc2) cross_entropy = tf.reduce_mean(-tf.reduce_sum(y_*tf.log(y_conv),reduction_indices=[1])) train_step = tf.train.AdamOptimizer(1e-4).minimize(cross_entropy) correct_prediction = tf.equal(tf.argmax(y_conv,1),tf.argmax(y_,1)) accuracy = tf.reduce_mean(tf.cast(correct_prediction,tf.float32))
4. 进行训练
通常在整点处用下一个batch进行简单测试效果,要先测试再训练
注意测试时keep_prob=1.0, 即不用dropout
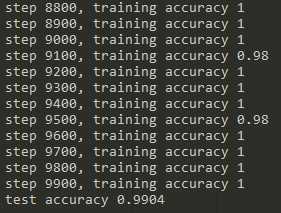
tf.global_variables_initializer().run() for i in range(20000): batch = mnist.train.next_batch(50) if i%100 == 0: train_accuracy = accuracy.eval(feed_dict={x:batch[0],y_:batch[1],keep_prob:10}) print("step %d, training accuracy %g" %(i,train_accuracy)) train_step.run(feed_dict={x:batch[0],y_:batch[1],keep_prob:0.5}) pritn("test accuracy %g" %accuarcy.eval(feed_dict={x:mnist.test.images,y_:mnist.test.labels,keep_prob:1.0}))
5.测试结果
相比于mlp的98%,卷积神经网络可以达到99%的精确度
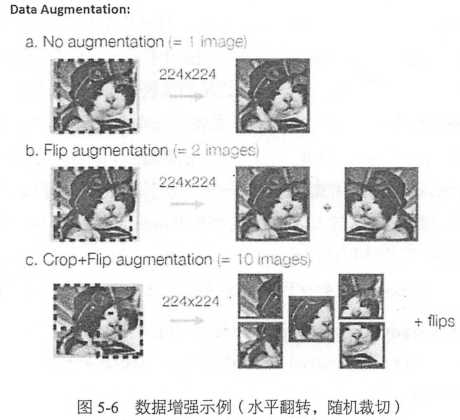
这里使用CIFAR-10数据集,相比于MNIST的手写数字识别(黑白),CIFAR中object识别更难(彩色)
60000张32x32的彩色图像,其中五万张训练,一万张测试,共有10类,每一张图片只有一个目标
相比简单版,这里使用的新技巧:
(1)对weights进行了L2的正则化
(2)对图片进行了翻转,随机剪切等数据增强,制造了更多样本,data augmentation
(3)在每个卷积-最大池化层后面使用了LRN层,增强了模型的泛化能力
首先要下载Tensorflow Models库,以便使用其中提供CIFAR-10数据的类
git clone https://github.com/tensorflow/models.git
cd models/tutorials/image/cifar10
然后载入一些常用库及一些参数定义,数据下载的默认路径
import cifar10,cifar10_input import tensorflow as tf import numpy as np import time max_steps = 3000 batch_size = 128 data_dir = ‘/tmp/cifar10_data/cifar-10-batches-bin‘
定义初始化weight的函数,这里给weight加了一个L2的loss,相当于做了一个L2的正则化处理
特征过多容易过拟合,可以通过减少特征或者惩罚不重要的特征来缓解这个问题,通常我们不知道该惩罚哪些特征的权重,而正则化就是帮助我们惩罚特征权重的,即特征的权重也会成为模型的损失函数的一部分。可以理解为,为了使用某个特征,我们需要付出loss的代价,除非这个特征非常有效,否则就会被loss上的增加覆盖效果。这样就可以筛选出最有效的特征,减少特征权重防止过拟合。这也即是奥卡姆剃刀法则,越简单的东西越有效。
一般来说,L1正则会制造稀疏的特征,大部分无用特征的权重会被置0,而L2正则会让特征的权重不过大,使得特征的权重比较平均。
用tf.add_to_collection把weight loss统一存到一个collection,名字为“losses”,在后面计算神经网络总体loss的时候会用上
def variable_with_weigth_loss(shape,stddev,w1): var = tf.Variable(tf.truncated_normal(shape,stddev=stddev)) if w1 is not None: weight_loss = tf.multiply(tf.nn.l2_loss(var),w1,name=‘weight_loss‘) tf.add_to_collection(‘losses‘,weight_loss) return var
使用cifar10类下载数据集,并解压,展开到默认位置
cifar10.maybe_download_and_extract()
再使用cifar10_input类中的distorted_inputs函数产生训练需要使用的数据,包括特征及label,每次执行都会生成一个batch_size数量的样本,这里对数据进行了data augmentation,具体细节可以看相应函数
数据增强包括随机的水平翻转,随机剪切一块24x24大小的图片,设置随机的亮度和对比度,以及对数据进行标准化(减去均值,除以方差,保证数据零均值,方差为1)
通过这些操作,可以获得更多的样本(带噪声)原来一张图片赝本可以变为多张图片,相当于扩大样本量,对提高准备率很有帮助
需要注意,对图像增强的操作需要耗费大量CPU时间,因此distorted_input使用了16个独立的线程来加速任务,函数内部会产生线程池,在需要使用时会通过tensorflow queue进行调度
images_train,labels_train = cifar10_input.distorted_inputs(data_dir=data_dir,batch_size=batch_size)
再通过cifar10_input.inputs函数生成测试数据,这里不需要进行太多处理,不需要对图片进行翻转或修改亮度,对比度,不过需要裁剪图片正中间的24x24大小的区块,并进行数据标准化操作
images_test,labels_test = cifar10_input.inputs(eval_data=True,data_dir=data_dir,batch_size=batch_size)
第一层卷积层的L2正则系数为0,bias也初始化为0
最大池化的尺寸和步长不一致,可以增加数据的丰富性
LRN最早见于AlexNet,解释说LRN层模仿了生物神经系统的“侧抑制”机制,对局部神经元的活动创建竞争环境,使得其中相应比较大的值变得相对更大,并抑制其他反馈较小的神经元,增强了模型的泛化能力。
LRN层对ReLU这种没有上限边界的激活函数会比较有用,因为它会从附近的多个卷积核的响应中挑选比较大的反馈,但不适合Sigmoid这种有固定边界并且能抑制过大值的激活函数
weight1 = variable_with_weigth_loss(shape=[5,5,3,64],stddev=5e-2,w1=0.0) kernel1 = tf.nn.conv2d(image_holder,weight1,[1,1,1,1],padding=‘SAME‘) bias1 = tf.Variable(tf.constant(0.0,shape=[64])) conv1 = tf.nn.relu(tf.nn.bias_add(kernel1,bias1)) pool1 = tf.nn.max_pool(conv1,ksize=[1,3,3,1],strides=[1,2,2,1],padding=‘SAME‘) norm1 = tf.nn.lrn(pool1,4,bias=1.0,alpha=0.001/9.0,beta=0.75)
第二层卷积层L2正则系数为0,bias初始化为0.1,而且调换了最大池化和LRN的顺序
weight2 = variable_with_weigth_loss(shape=[5,5,64,64],stddev=5e-2,w1=0.0) kernel2 = tf.nn.conv2d(norm1,weight2,[1,1,1,1],padding=‘SAME‘) bias2 = tf.Variable(tf.constant(0.1,shape=[64])) conv2 = tf.nn.relu(tf.nn.bias_add(kernel2,bias2)) norm2 = tf.nn.lrn(conv2,4,bias=1.0,alpha=0.001/9.0,beta=0.75) pool2 = tf.nn.max_pool(norm2,ksize=[1,3,3,1],strides=[1,2,2,1],padding=‘SAME‘)
两层全连接层
我们希望这个全连接层不要过拟合,因此设了一个非0的weight loss为0.004,让这一层的所有参数都被L2正则所约束,bias初始化为0.1
reshape = tf.reshape(pool2,[batch_size,-1])
dim = reshape.get_shape()[1].value
weight3 = variable_with_weigth_loss(shape=[dim,384],stddev=0.04,w1=0.004)
bias3 = tf.Variable(tf.constant(0.1,shape=[384]))
local3 = tf.nn.relu(tf.matmul(reshape,weight3)+bias3)
weight4 = variable_with_weigth_loss(shape=[384,192],stddev=0.04,w1=0.004)
bias4 = tf.Variable(tf.constant(0.1,shape=[192]))
local4 = tf.nn.relu(tf.matmul(local3,weight4)+bias4)
最后一层,不计L2正则,正态分布的标准差设为上一个隐含层的节点数的倒数,而且这里没有使用softmax作为输出,而是放在了计算loss的部分
weight5 = variable_with_weigth_loss(shape=[192,10],stddev=1/192.0,w1=0.0) bias5 = tf.Variable(tf.constant(0.0,shape=[10])) logits = tf.add(tf.matmul(local4,weight5),bias5)
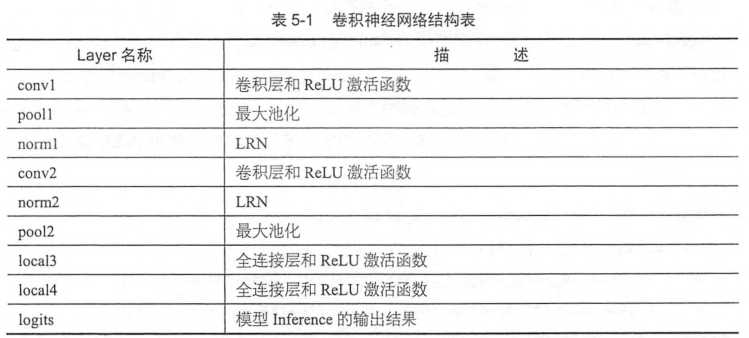
以上完成了整个网络的inference部分,如下表,是整个神经网络从输入到输出的流程,可以发现,设计CNN主要就是安排卷积层,池化层,全连接层的分布和顺序,以及其中超参数的设置,trick的使用等。
设计性能良好的CNN是有一定规律可循的,但是想要针对某个问题设计最合适的网络结构是需要大量实践摸索的
开始计算loss
使用tf.add_n将整体losses的collection中全部loss求和,得到最终的loss,其中包括cross entropy loss,还有后面两个全连接层中weight的L2 loss
这里in_top_k表示label在不在top_k结果中,这里使用tf.nn.in_toop_k函数求输出结果中top k的准确率
def loss(logits,labels): labels = tf.cast(labels,tf.int64) cross_entropy = tf.nn.sparse_softmax_cross_entropy_with_logits( logits=logits,labels=labels,name=‘cross_entropy_per_example‘) cross_entropy_mean = tf.reduce_mean(cross_entropy,name=‘cross_entropy‘) tf.add_to_collection(‘losses‘,cross_entropy_mean) return tf.add_n(tf.get_collection(‘losses‘),name=‘total_loss‘) loss = loss(logits,label_holder) train_op = tf.train.AdamOptimizer(1e-3).minimize(loss) top_k_op = tf.nn.in_top_k(logits,label_holder,1) sess = tf.InteractiveSession() tf.global_variables_initializer().run()
启动图片数据增强的线程队列,这里一共使用了16个线程来进行加速,注意,如果这里不启动线程,那么后续的inference及训练操作都是无法开始的
tf.train.start_queue_runners()
开始正式训练,会输出一些时间的信息
for step in range(max_steps): start_time = time.time() image_batch,label_batch = sess.run([images_train,labels_train]) _,loss_value = sess.run([train_op,loss], feed_dict={image_holder:image_batch,label_holder:label_batch}) duration = time.time() - start_time if step % 10 ==0: examples_per_sec = batch_size / duration sec_per_batch = float(duration) format_str=(‘step %d,loss=%.2f (%.1f examples/sec; %3f sec/batch‘) print(format_str %(step,loss_value,examples_per_sec,sec_per_batch))
进行测试
执行top_k_op计算模型在这个batch的top1上预测正确的样本数,然后汇总所有预测正确的结果,求得全部测试样本中预测正确的数量
num_examples = 10000 import math num_iter = int(math.ceil(num_examples/batch_size)) true_count = 0 total_sample_count = num_iter * batch_size step = 0 while step < num_iter: image_batch,label_batch = sess.run([images_test,labels_test]) predictions = sess.run([top_k_op],feed_dict={image_holder:image_batch, label_holder:label_batch}) true_count += np.sum(predictions) step += 1 precision = true_count /total_sample_count print(‘precision @ 1 = %.3f‘ % precision)
实验结果
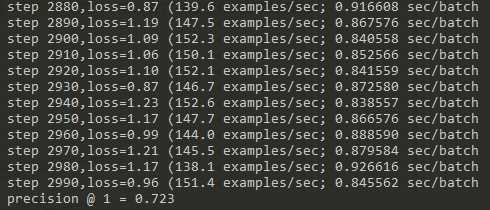
持续增加max_steps,可以期望准确率逐渐增加
如果max_steps比较大,推荐使用学习速率衰减的SGD进行训练,这样训练过程中能达到的准确率峰值会比较高
数据增强在训练中作用很大,它可以给单幅图增加多个副本,提高图片的利用率,防止对某一张图片结构的学习过拟合。这刚好是利用率图片数据本身的性质,图片的冗余信息量比较大,因此可以制造不同的噪声并让图片依然可以被识别出来。如果神经网络可以克服这些噪声并准确识别,那么它的泛化性能必然会很好。
数据增强大大增加了样本量,而数据量的大小恰恰是深度学习最看重的,深度学习可以再图像识别上领先其他算法的一大因素就是它对海量数据的利用效率非常高。用其他算法,可能在数据量达到一定程度时,准确率就不再上升了,而深度学习只要提供足够多的样本,准确率基本可以持续提升,所以说它是最适合大数据的算法
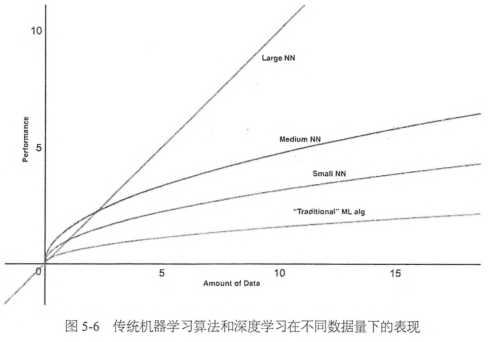
前面的卷积层主要是做特征提取的工作,知道最后的全连接层才开始对特征进行组合匹配,并进行分类。
卷积层的训练相对于全连接层更复杂,训练全连接层基本是进行一些矩阵乘法运算,而目前卷积层的训练基本依赖于cuDNN的实现
标签:池化 truncate 图像 nta drop 利用 完成 否则 方式
原文地址:http://www.cnblogs.com/lainey/p/7507213.html