标签:2-2 name cst cstring 技术 scan 题意 不同 双向
给定n个城市的货物买卖价格, 然后给定n-1条道路,每条路有不同的路费, 求出从某两个城市买卖一次的最大利润。
利润 = 卖价 - (买价 + 路费)
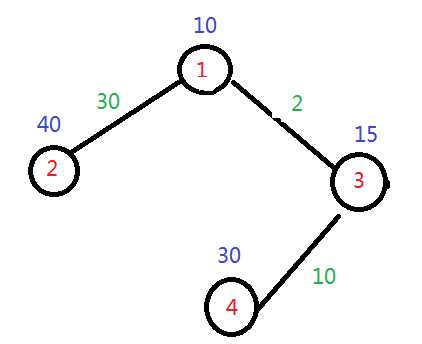
样例数据, 最近是从第一个点买入, 第4个点卖出, 利润为8
1.如果一条边连接(u,v),路费为cost ,城市买卖价格用P( )表示, 那么他的边权就表达为(P(v) - P(u) - cost).
2.我们可以假设有一个起点。他连接着所有的点,边权为0。
3.那么如果从这个点出发的话, 就等于是把所有的城市都尝试作为买入城市
4.然后只要做一次允许有副权的SPFA最短路算法就能算出正确答案了。
#include <cstdio> #include <vector> #include <queue> #include <cstring> using namespace std; const int maxn = 1e5 + 7; int T,n; int d[maxn], P[maxn], vis[maxn]; struct Node{ int num; int dis; Node(int a = 0, int b = 0):num(a), dis(b){} }; vector<Node> G[maxn]; int spfa(){ memset(d,-1,sizeof(d));//因为要做最长路, 所以把初始值设为-1。 memset(vis,0,sizeof(vis)); for(int i = 1; i <= n; i++) G[0].push_back(Node(i,0)); // 虚拟一个起点,练向所有的点。 queue<int> q; d[0] = 0; q.push(0); vis[0] = 1; while(!q.empty()){ int u = q.front(); for(int i = 0; i < G[u].size(); i++){ int v = G[u][i].num; if(d[v] < d[u] + G[u][i].dis){ d[v] = d[u] + G[u][i].dis; if(!vis[v]){ q.push(v); vis[v] = 1; } } } q.pop(); vis[u] = 0; } int ans = -1; for(int i = 1; i <= n; i++){ ans = max(ans,d[i]); } // puts(""); return ans; } void init(int n){ for(int i = 0; i <= n; i++ ) G[i].clear(); } int main(){ scanf("%d", &T); while(T--){ scanf("%d", &n); for(int i = 1; i <= n; i++){ scanf("%d", &P[i]); } for(int i = 0; i < n - 1; i++){ int u , v, cost; scanf("%d %d %d",&u, &v, &cost); G[u].push_back(Node(v,P[v] - P[u] - cost));//双向边 G[v].push_back(Node(u,P[u] - P[v] - cost)); } printf("%d\n",spfa()); init(n);//初始化临接表 } }
hdu 6201 transaction (最短路变形——带负权最长路)
标签:2-2 name cst cstring 技术 scan 题意 不同 双向
原文地址:http://www.cnblogs.com/Jadon97/p/7516643.html