标签：des style blog class code java
perspective projection
title: perspective projection tags: ["openGL", "Markdown", "mathjax"] notebook: notes
关于投影变换
我们先介绍一个概念,NDC(Normalized Device
Coordinates).我们在opengl右手坐标系里建立的模型都会映射到NDC.所以所有的点坐标的分量都会在[-1,1]间,超出的将被clip掉.尔后,NDC将坐标映射到viewport(视口),那为什么会有NDC这个中间产物?计算方便.不管是在后面映射视口,还是矩阵计算.特别要注意的是NDC是左手坐标系
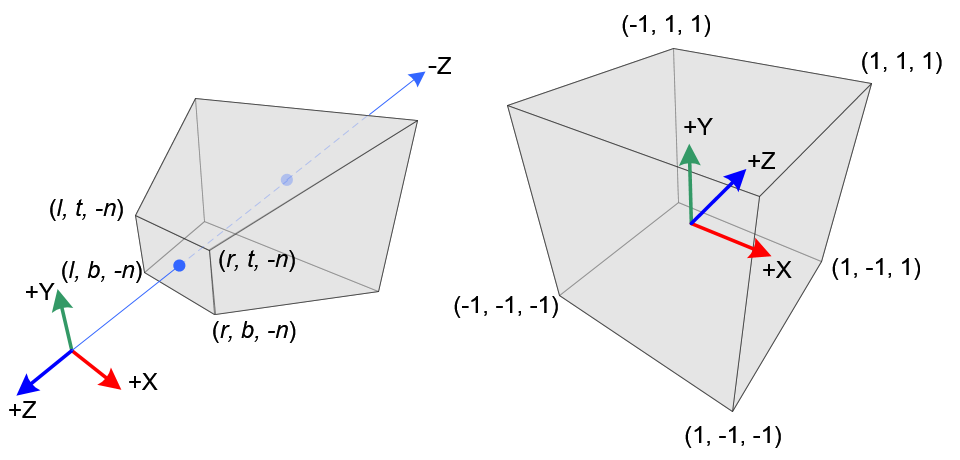
左为perspective projection,这跟我们看到的真实世界是一样的原理.有很强的3D视感.而右边.则是ortho
projection,如果你学过工程制图.想必也很熟悉.没有近大远小的概念 下面,我们试着计算投影公式.这里我们用一下缩写
\cases{l=left \\ r=right \\ f=far \\ n=near \\ b=bottom \\ t=top}
将下图的立方体空间映射到NDC空间.假设下面空间中一点(x,y,z,w) ,求(x_{ndc},y_{ndc},z_{ndc},w_{ndc})
\frac{r-l}{2}=\frac{x-l}{x_{ndc}+1} => x_{ndc}=\frac{2}{r-l}x+\frac{l+r}{l-r}\
y_{ndc},z_{ndc} 同理,很容易得到矩阵 \left[ \begin{array}{cccccccccccccc} \frac{2}{r-l}&0&0& \frac{l+r}{l-r} \\ 0&\frac{2}{t-b}&0& \frac{b+t}{b-t} \\ 0&0&\frac{2}{f-n}& \frac{n+f}{n-f} \\ 0&0&0&1 \\ \end{array} \right]
同样,根据等比公式,得到如下公式,我们假设还一组中间变量(x_{p},y_{p},z_{p},w_{p}) ,代表(x,y,z,w) 映射到near面上的点.(注意,这里还没有转换到NDC) \cases{\frac{z}{x}=\frac{-n}{x_p}\\ \frac{z}{y}=\frac{-n}{y_p}\\ z_p=n} => \cases{x_p=\frac{-nx}{z} \\ y_p=\frac{-ny}{z} \\ z_p=n}
投影影射90%的工作,接下来我们需要将投影点再映射到NDC
以x_p 为例 \cases{al+b=-1\\ ar+b=1} => \cases{a=\frac{2}{r-l}\\ b=\frac{l+r}{l-r}}
NDC里的映射是用这个线性函数
x_{ndc}=\frac{2}{r-l}x_p+\frac{l+r}{l-r}=\frac{2}{r-l}\frac{-nx}{z}+\frac{l+r}{l-r}
z_{x_{ndc}}=\frac{-2n}{r-l}_x + \frac{l+r}{l-r} z
是不是有点感觉了
\left[ \begin{array}{cccccccccccccc} \frac{-2n}{r-l}&0&\frac{l+r}{l-r}&0\\ 0&0&0&0\\ 0&0&0&0\\ 0&0&0&0\\ \end{array} \right]\left[ \begin{array}{cccccccccccccc} x\\ 0\\ 0\\ 1\\ \end{array} \right] =\left[ \begin{array}{cccccccccccccc} {x_{ndc}}*z\\ 0\\ 0\\ 0\\ \end{array} \right]\
同理,得到y_p
\left[ \begin{array}{cccccccccccccc} \frac{-2n}{r-l}&0&\frac{l+r}{l-r}&0\\ 0&\frac{-2b}{t-b}&\frac{b+t}{b-t}&0\\ 0&0&0&0\\ 0&0&0&0\\ \end{array} \right]\left[ \begin{array}{cccccccccccccc} x\\ y\\ 0\\ 1\\ \end{array} \right]=\left[ \begin{array}{cccccccccccccc} x_{ndc} * z\\ y_{ndc}*z\\ 0\\ 0\\ \end{array} \right]\
到这个地方我得停住说点别的. 上面公式中,我们求到的点都是放大了当前点的z倍. 所以必须除以z.而除z这个操作,学名叫 perspective
divide,这个操作不用你操心,opengl 管线中会自动处理.自动除z??不对啊.我们在投影变换完后z_{npc}
轴都在一个平面了.还原不出原始的z了啊! 人类的智慧是无穷的.我们可以将z复制到在w分量上,所以管线中的perspective
divide操作其实就是除以w.而w=z.这样我们就得到矩阵第4行的值.要还原投影点,perspective
divide将(x_p,y_p,z_p)
分别除以z(z=w).得到的点为(x_p/z,y_p/z,z_p/z,z)
, 请特别注意它们的下标!!要除的z是最原始点的z. 我们尝试构造第三行.
A,B,C,D
\left[ \begin{array}{cccccccccccccc} \frac{-2n}{r-l}&0&\frac{l+r}{l-r}&0\\ 0&\frac{-2b}{t-b}&\frac{b+t}{b-t}&0\\ A&B&C&D\\ 0&0&1&0\\ \end{array} \right]\left[ \begin{array}{cccccccccccccc} x\\ y\\ z\\ 1\\ \end{array} \right]=\left[ \begin{array}{cccccccccccccc} x_{ndc_z} \\ y_{ndc_z}\\ z\\ z\\ \end{array} \right]\
$$
Ax+By+Cz+D=z_{ndc}*z
\cases{ Ax+By+Cn+D=-1_n \\ Ax+By+Cf+D= 1_f }
\left[ \begin{array}{cccccccccccccc} \frac{-2n}{r-l}&0&\frac{l+r}{l-r}&0\\ 0&\frac{-2b}{t-b}&\frac{b+t}{b-t}&0\\ 0&0&\frac{f+n}{f-n}&\frac{2fn}{f-n}\\ 0&0&1&0\\ \end{array} \right]
frustum 1 介绍的方法,需要6参数.而且不太直观.下面介绍另一种常见的构造投影变换的方法. 不管用什么方法,只要参数能够确定唯一的一个frustum.就行. 我们先看一张网上淘来的图..
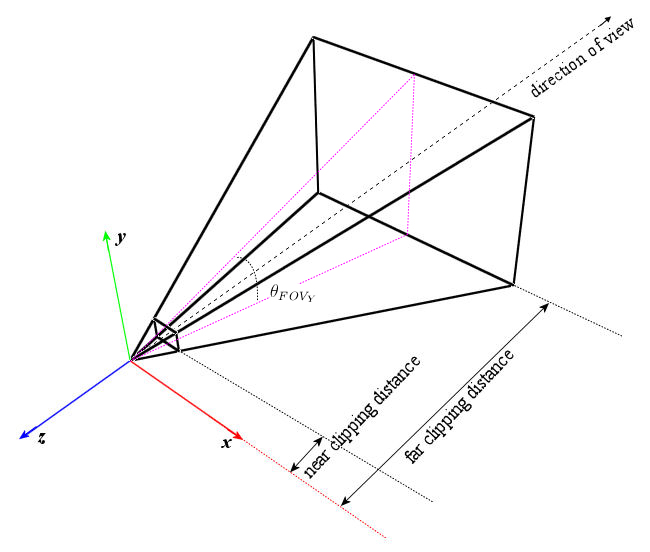
fov=field of view.视野,我们假定它为相机上平面与下平面的夹角\theta .
near,跟 far 就很显然了. 我们还需要一个参数.那就是近平面的宽高比值记作ar(aspect ratio).
好了.参数有了. \theta ,ar,n,f, 下面求矩阵 因为z_{ndc} 的投影变换只与n,f有关,上面frustum 1中已经有公式.不再赘述. 比如先求y_{ndc} ,我们垂直从+x看到-x.很容易得到如下公式 \frac{y_p}{n}=\frac{y}{z} => y_p=\frac{y}{z}\dot{}n
\left[ \begin{array}{cccccccccccccc} \frac{1}{ar\dot{}tan\frac{\theta}{2}}&0&0&0\\ 0&\frac{1}{tan\frac{\theta}{2}}&0&0\\ 0&0&\frac{f+n}{f-n}&\frac{2fn}{f-n}\\ 0&0&1&0\\ \end{array} \right]
10分钟入门opengl投影变换推导(内含mathjax公式),布布扣,bubuko.com
10分钟入门opengl投影变换推导(内含mathjax公式)
标签：des style blog class code java
原文地址：http://www.cnblogs.com/syncg/p/3719912.html
