标签:clu closed src str 深度 main http 同时存在 long

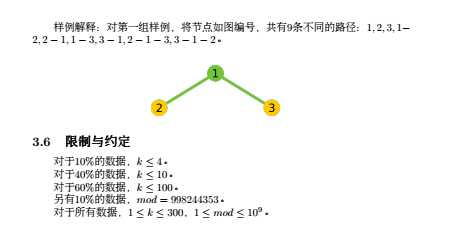
这道题当时dfs+打表过了3个点,还算可以。
当时推测的是递推/数学,然而正解是一个类似于DP的递推。
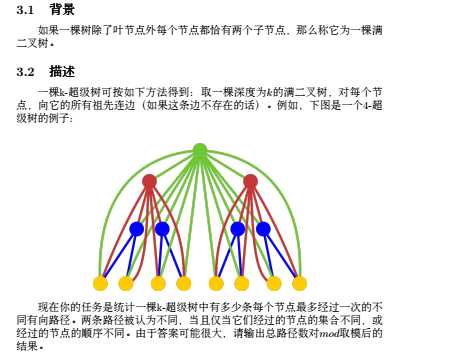
我们设定f[i][j]为深度为i的树中同时存在j条边,且所有边无任何两条有公共点,不必包含所有点的情况数。确实很绕也貌似没有太大的实际意义(至少我没有理解到),那么我们的转移方程便如下:
j,k为上一步的两个状态,num为f[i-1][j]*f[i-1][j],即代表新树的两棵子树
通过新节点连接某个子树的两个路径: f[i][j+k-1]+=num*(max(0ll,j*(j-1))+max(k*(k-1),0ll)); 通过新节点连接分别位于两个子树的两个路径: f[i][j+k-1]+=num*j*k*2; 无任何操作: f[i][j+k]+=num; 将新节点连接在每一个路径的起点(重点): f[i][j+k]+=num*(j+k)*2;
新节点自身也算一个路径: f[i][j+k+1]+=num;
1 #include<iostream> 2 #include<cstdlib> 3 #include<cstdio> 4 #include<cstring> 5 #include<queue> 6 #include<algorithm> 7 #include<cmath> 8 #define N 305 9 using namespace std; 10 long long n,mod; 11 long long f[N][N]; 12 int main() 13 { 14 scanf("%lld%lld",&n,&mod); 15 f[1][0]=f[1][1]=1; 16 bool yx=1; 17 for(long long i=2;i<=n;i++) 18 { 19 int to=n-(i-1)+1; 20 if(yx) 21 { 22 if(1<<(i-1)-1<0)yx=0; 23 else if(to>((1<<(i-1))-1))to=(1<<(i-1))-1; 24 } 25 for(long long j=0;j<=to;j++) 26 { 27 for(long long k=0;k<=to;k++) 28 { 29 long long num=f[i-1][j]*f[i-1][k]; num%=mod; 30 if(j+k-1>304)continue; 31 f[i][j+k-1]+=(num*(max(0ll,j*(j-1))+max(k*(k-1),0ll)))%mod; f[i][j+k-1]%=mod; 32 f[i][j+k-1]+=(num*j*k*2)%mod; f[i][j+k-1]%=mod; 33 if(j+k>304)continue; 34 f[i][j+k]+=num; f[i][j+k]%=mod; 35 f[i][j+k]+=(num*(j+k)*2)%mod; f[i][j+k]%=mod; 36 if(j+k+1>304)continue; 37 f[i][j+k+1]+=num; f[i][j+k+1]%=mod; 38 39 40 } 41 } 42 } 43 printf("%lld\n",f[n][1]%mod); 44 return 0; 45 }
不得不说这道题真心挺难,尤其是状态转移方程,简直不是人类能想出来的其实是我太弱,人家育才有7个人A了。
标签:clu closed src str 深度 main http 同时存在 long
原文地址:http://www.cnblogs.com/liutianrui/p/7528420.html