标签：小结 bit space center 可以转化 pow 求逆 original 16px
1.乘法逆元定义：在wiki中也叫倒数，当然是% p 后的，其实就是倒数。如果ax≡1(mod p),且gcd（a，p）=1（a与p互质），则称a关于模p的乘法逆元为x。
在求解除法取模问题(a/b)%m时，我们可以转化为(a%(b∗m))/b，
但是如果b很大，则会出现爆精度问题，所以我们避免使用除法直接计算。
可以使用逆元将除法转换为乘法：
假设b存在乘法逆元，即与m互质（充要条件）。设c是b的逆元，即b∗c≡1(modm)，那么有a/b=(a/b)∗1=(a/b)∗b∗c=a∗c(modm)
即，除以一个数取模等于乘以这个数的逆元取模。
2.费马小定理：假如a是一个整数，p是一个质数，那么
是a的倍数，可以表示为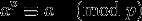
如果a不是p的倍数，也可以写成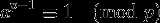
3.拓展欧几里得：已知整数a，b，拓展欧几里得算法可以在求得a，b的最大公约数的同时，能找到整数x，y（其中一个很可能是负数），使它们满足贝祖等式
4.分析乘法逆元：ax≡1 (mod p) 这个等式用中文描述就是 a乘一个数x并模p等于1，即 a%p * x%p = res, res % p=1;看上去就是同余定理的一个简单等式 - -。那么问题来了。
5.为什么可以用扩展欧几里得求得逆元？我们知道模就是余数，比如12%5=12-5*2=2，18%4=18-4*4=2 那么ax ≡ 1(mod p)即 ax - yp =1.把y写成+的形式就是ax+py=1，为方便理解下面，我们把p写成b就是ax + by=1。就表示x是a的模b乘法逆元，y是b的模a乘法逆元。然后就可以用欧几里得求。
6.乘法逆元有什么用？做题时如果结果过大一般都会让你模一个数，确保结果不是很大，而这个数一般是1e9+7，而且这个数又是个素数，加减乘与模运算的顺序交换不会影响结果，但是除法不行。有的题目要求结果mod一个大质数，如果原本的结果中有除法，比如除以a,那就可以乘以a的逆元替代。（除一个数等于乘它的倒数，虽然这里的逆元不完全是倒数，但可以这么理解，毕竟乘法逆元就是倒数的扩展）。
拓展欧几里得求逆元代码：【时间复杂度为O(logn)】
#include<bits/stdc++.h> using namespace std; typedef long long ll; void exgcd(ll a,ll b,ll& d,ll& x,ll& y) { if(!b) { d = a; x = 1; y = 0; } else{ exgcd(b, a%b, d, y, x); y -= x*(a/b); } } ll inv(ll a, ll p) { ll d, x, y; exgcd(a, p, d, x, y); return d == 1 ? (x+p)%p : -1; } int main() { ll a,p; while(1) { scanf("%lld %lld",&a,&p); printf("%lld\n",inv(a,p)); } }
费马小定理求逆元代码：【O（log2N），在几次测试中，常数似乎较上种方法大】
ll power_mod(ll a, ll b, ll mod) { ll ans = 1; while (b) { if (b & 1) ans = ans * a % mod; a = a * a % mod; b >>= 1; } return ans; } inv2 = power_mod(a, mod - 2, mod);
欧拉定理求逆元代码：【O(√n)，即求出单个欧拉函数的值】
int eurler_phi(int n) { int res = n; for(int i = 2; i * i <= n; i++){ if(n % i == 0){ res = res / i * (i - 1); while(n % i == 0) n /= i; } } if(n != 1) res = res / n * (n - 1); return res; }
参考：乘法逆元小结+ 逆元的几种求法（扩展欧几里得，费马小定理或欧拉定理，特例，打表等）+ ACM数论之旅6---数论倒数，又称逆元（我整个人都倒了(￣﹏￣)）
标签：小结 bit space center 可以转化 pow 求逆 original 16px
原文地址：http://www.cnblogs.com/Roni-i/p/7533665.html
