标签:模拟 ges main 条件 排序 整数 正整数 决定 return
餐厅(restaurant)
【问题描述】
小R最近在玩一款模拟餐厅打工的游戏,其中有一个叠盘子的小游戏小R很喜欢。这个小游戏是这样的:有一个放盘子的机器会在一条直线上运动,机器里装着n个盘子,其中第i个盘子半径为ri,并且如果要放下该盘子,盘子的中心必须放在直线上xi的位置上,小R可以决定放下哪些盘子和放下这些盘子的顺序,盘子可以放在空位上,或者叠在一个上面没有其他盘子的盘子上,但要求被叠的盘子必须包含要叠上去的盘子。小R想要让叠出的盘子尽量高,请你计算出最高的一叠最多能叠几个盘子。
【输入格式】
第一行一个正整数n,表示盘子数。
接下来n行,每行两个正整数ri和xi。
【输出格式】
输出一个整数,表示答案。
【样例输入】
3
3 5
2 4
2 6
【样例输出】
2
【数据范围】
对于20%的数据,n<=10;
对于50%的数据,n<=1,000;
对于100%的数据,n<=100,000,ri,xi<=109。
【题解】
题目开始不太好理解,样例解释如图(可以不按编号顺序)
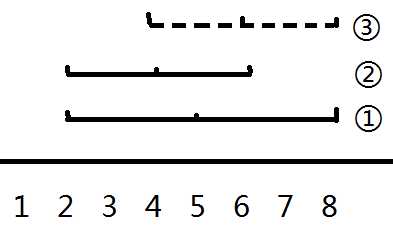
对于满足条件的堆叠方式,盘子的右端点一定是一个不下降序列,因此先按盘子的右端点排序。
对于左端点来说,同样是一个不下降序列,因此对按右端点排序后的盘子的左端点求最长不下降子序列即可。
【代码实现】
1 #include<algorithm> 2 #include<stdio.h> 3 int n,r,x; 4 struct data{ 5 int l,r; 6 }p[100000]; 7 bool cmp(data a,data b){return a.r==b.r?a.l<b.l:a.r>b.r;} 8 int ans=0,best[100000]; 9 int bin(int num){ 10 int l=0,r=ans; 11 while(l<=r){ 12 int mid=(l+r)/2; 13 if(best[mid]==num){while(best[mid]==num)mid++;return mid;} 14 if(best[mid]<num)l=mid+1; 15 if(best[mid]>num)r=mid-1; 16 } 17 return l; 18 } 19 int up(){ 20 best[0]=p[0].l; 21 for(int i=1;i<n;i++){ 22 if(p[i].l>=best[ans]){best[++ans]=p[i].l;continue;} 23 best[bin(p[i].l)]=p[i].l; 24 } 25 return ans+1; 26 } 27 int main(){ 28 freopen("restaurant.in","r",stdin); 29 freopen("restaurant.out","w",stdout); 30 scanf("%d",&n); 31 for(int i=0;i<n;i++){ 32 scanf("%d%d",&r,&x); 33 p[i].l=x-r,p[i].r=x+r; 34 } 35 std::sort(p,p+n,cmp); 36 printf("%d",up()); 37 return 0; 38 }
NOIP模拟赛(2017.9.15) -餐厅(restaurant)
标签:模拟 ges main 条件 排序 整数 正整数 决定 return
原文地址:http://www.cnblogs.com/OMG-link/p/7534961.html