标签:6.2 坐标 pen 圆心 height 观察 -- alt fine
背景:
站军姿是一件非常痛苦的事情,特别当教官在附近游荡时。
题目描述:
有两个教官,每个教官又一个位置坐标和一个视线范围,该教官能够观察到以该位置为圆心,给定半径的一个圆,你需要求出有多大面积的地方在两个教官的视线范围内。
由于教官四处游荡,因此你需要实现多组数据。
输入描述:
第一行一个数T表示数据组数。
接下来T行每行六个实数,分别为x1,y1,r1,x2,y2,r2,代表两个教官的各项参数。
输出描述:
每组数据输出一行表示答案,答案保留三位小数。
样例输入:
1
3 3 1 3 3 0.5
样例输出:
3.142
数据范围:
对于10%的数据,两圆相离
对于10%的数据,两圆为包含关系
对于另外40%的数据,满足T=1且0≤|x|,|y|,r≤5
对于100%的数据,T≤10,0≤|x|,|y|,r≤le5
思路:
分为 相离,相交,内含。三种情况,一一判定即可。
相交的话麻烦一点:
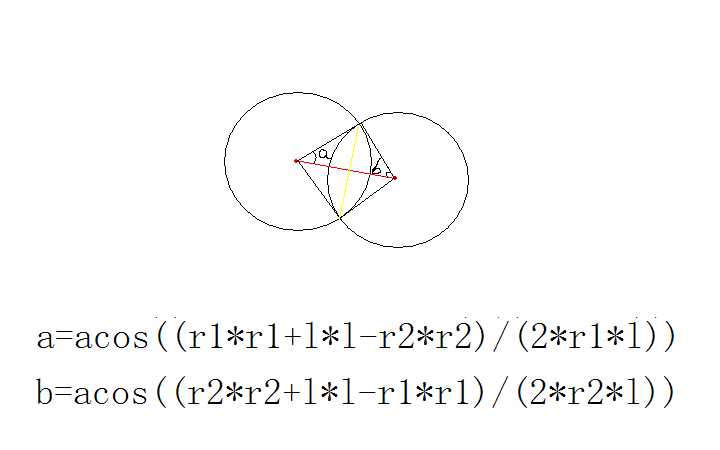 用扇形的面积减去三角形面积,就是弓形面积,减去弓形面积即可。
用扇形的面积减去三角形面积,就是弓形面积,减去弓形面积即可。
#include<iostream> #include<cstdio> #include<queue> #include<algorithm> #include<cstring> #include<cmath> using namespace std; #define N 1000009 double x11,y11,x2,y2,r1,r2; double L,ans,pi=3.1415926; int main() { freopen("standing.in","r",stdin); freopen("standing.ans","w",stdout); int T; scanf("%d",&T); while(T--) { cin>>x11>>y11>>r1>>x2>>y2>>r2; L=(x11-x2)*(x11-x2)+(y11-y2)*(y11-y2); if(L>=(r1+r2)*(r1+r2)) { ans=(double)(pi*r1*r1+pi*r2*r2); printf("%.3lf",ans); }else if(L<=(r1-r2)*(r1-r2)) { ans=(double)(pi*max(r1,r2)*max(r1,r2)); printf("%.3lf",ans); }else { double all=(pi*r1*r1+pi*r2*r2); double a=acos((L+r1*r1-r2*r2)/(2*sqrt(L)*r1)); double s=r1*r1*a- r1*r1*sin(a)*cos(a); all-=s; a=acos((L+r2*r2-r1*r1)/(2*sqrt(L)*r2)); s=r2*r2*a- r2*r2*sin(a)*cos(a); all-=s; printf("%.3lf",all); } } return 0; }
样例:
2
输入:
2
1 0 2
1 1 2
0 0 1
3 3 1
输出:
16.524
6.283
标签:6.2 坐标 pen 圆心 height 观察 -- alt fine
原文地址:http://www.cnblogs.com/CLGYPYJ/p/7536432.html