标签:9.png href 结果 利用 ges alt col def turn
0)引论
左堆的合并,插入,删除最小的时间复杂度为O(logN)。二项队列就是为了对这些结果进一步提高的一种数据结构。利用二项队列,这三种操作的最坏时间复杂度为O(logN),但是插入的平均时间复杂度为O(1)。
1)二项队列
二项队列不是一棵树,它是一个森林,由一组堆序的树组成的深林,叫做二项队列。
二项队列有几个性质比较重要
(a) 每一颗树都是一个有约束的堆序树,叫做二项树
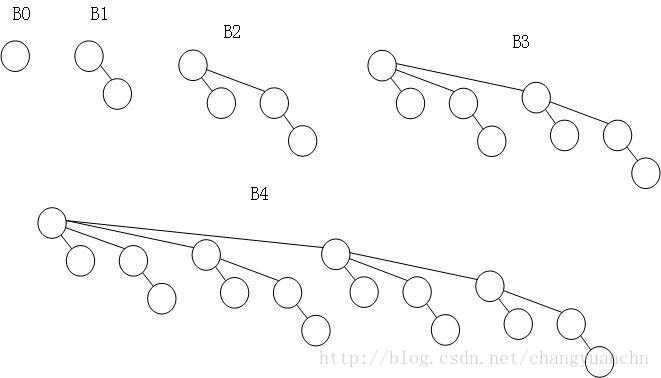
(b) 高度为k的第k个二项树Bk由一个根节点和B0, B1, .......B(k-1)构成
(c) 高度为k的二项树的结点个数为2^k
我们可以用二项树的结合表示任意大小的优先队列。例如,大小为13的优先队列就可以用B3,B2,B0来表示,二进制的表示为1101。对此,我深表怀疑二项队列是不是受二进制的启发而产生的。
2)二项队列的操作
查找最小项:只需要查找每个二项树的根节点就可以了,因此时间复杂度为O(logN)。
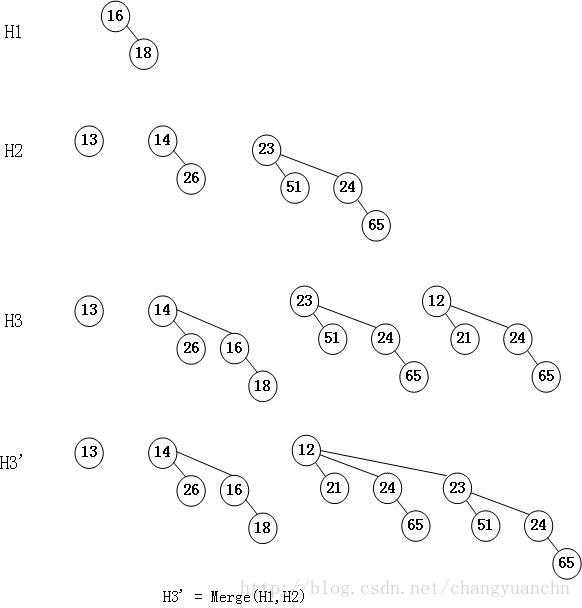
合并:通过把两个队列相加在一起完成。因为有O(logN)棵树,所以合并的时间复杂度也是O(logN)。
插入:插入也是一种合并,只不过是把插入的结点当做B0。虽然感觉插入的时间复杂度是O(logN),但是实际是O(1),因为有一定的概率是被插入的二项队列没有B0。
删除最小:在根结点找到最小值,然后把最小值所在的树单独拿出分列为二项队列,然后把这个新的二项队列与原二项队列进行合并。每一个过程的时间复杂度为O(logN)。故加起来的时间复杂度仍为O(logN)。
这些操作归根结底是合并Merge。
3)二项队列的代码实现
二项队列声明:
typedef struct BinNode *Position; typedef struct BinNode *BinTree; typedef struct Collection *BinQueue; struct BinNode { ElementType Element; Position LeftChild; Position Sibling; }; struct Collection { int CurrentSize; BinTree TheTrees[MaxTree]; }
首先定义了树BinNode,然后定义了森林Collection。
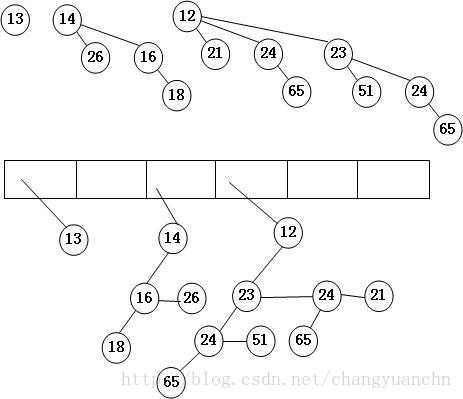
注意:
指针数组的大小一般至少是二项队列中二项树数目×2+1;
数组第 i 号索引处,存储的是高度为 i 的二项树。如,第0号索引,存储高度为0的二项树,该二项树只有一个结点,结点权值为13;
每棵二项树由左孩子右兄弟的链表保存;
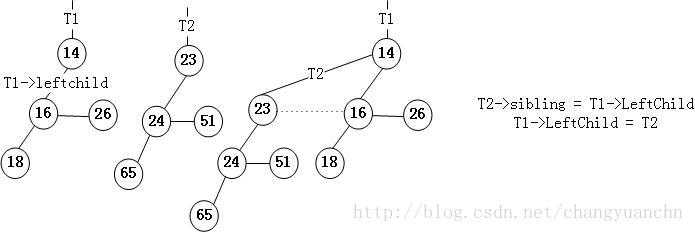
合并树本质是指针的变动。当然要对两个二项树做好变换。
标签:9.png href 结果 利用 ges alt col def turn
原文地址:http://www.cnblogs.com/anzhi/p/7536443.html