标签:注意 ora comm 生命力 如图所示 png 网络 mon 混合图欧拉回路
对于图 $G = (V, E)$ , 若存在一条回路 $P$ , 经过所有边有且仅有一次, 则成 $P$ 为 $G$ 的一条欧拉回路, $G$ 称为欧拉图.
对于图 $G = (V, E)$ , 若存在一条路径 $P$ , 经过所有边有且仅有一次, 则称 $P$ 为 $G$ 的一条欧拉路径, $G$ 称为半欧拉图.
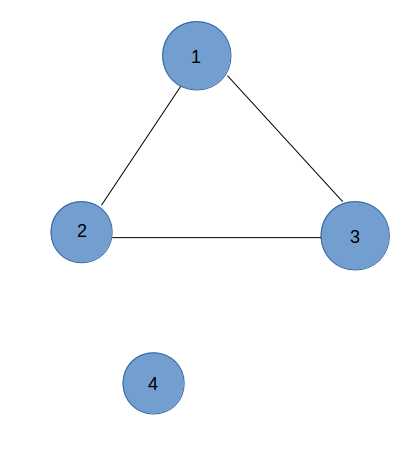
如图所示, 路径 $1 \rightarrow 2 \rightarrow 3 \rightarrow 1$ 就是一条欧拉回路.
上述的定义有几个值得注意的地方:
① 欧拉图 $G$ 不一定要连通, 因为可能有孤立点的存在, 例如上图的 4 号点. 我们通常排除掉孤立点来考察这张图.
② 注意 $G$ 可能是无向图, 可能是有向图, 也可以是混合图.
在上述的概念中, 最为核心的概念是欧拉回路, 这在之后会有所体现.
给出了欧拉回路的相关定义之后, 我们应该要有所追求地给自己几个小小的探究目标.
对于一般的探究思路, 我们要依次研究存在性, 个数, 求任意解层次的问题.
在欧拉图中, 存在性层次就包括了欧拉图的判定, 与构造欧拉回路的方法; 个数层次就是求解欧拉回路的个数, 在本文中忽略.
我们考虑先探究 $G$ 为无向图时的情况.
当无向图 $G$ 为欧拉图时, $G$ 明显是连通图. 而且注意到每个点的一条入边与一条出边相对应, 所以所有点的度数都为偶数.
于是我们得到了这样一个结论: 无向图 $G$ 为欧拉图 $\Rightarrow$ $G$ 连通, 且任意一个点的度数为偶数.
我们猜测 "$G$ 连通, 且任意一个点的度数为偶数" 不仅是必要条件, 而且也是充分条件.
经过大量地实验, 我们发现似乎真的是如此.
定理1 (无向欧拉图判定定理)
无向图 $G$ 为欧拉图 $\Leftrightarrow$ $G$ 为连通图, 且所有点的度数为偶数.
证明
由上述的推导过程, 我们知道必要性显然. 下面证明充分性, 即 " 无向图 $G$ 为欧拉图 $\Leftarrow$ $G$ 连通, 且任意一个点的度数为偶数. "
假设 $G$ 中不存在回路, 又因为 $G$ 连通且不存在孤立点, 所以 $G$ 是一棵树, 所以 $|E| = |V| - 1$ . 由于 $G$ 为连通图, 且所有点的度数为偶数, 所以 $\forall i \in V, d_i \ge 2$ . 根据边数与度数的关系, $|E| = \frac{1}{2} \sum_{k \in V} d_k \ge |V|$ , 这与 $|E| = |V| - 1$ 矛盾. 所以 $G$ 中一定存在回路.
不妨设 $G$ 中最长的回路为 $C$ , 下面尝试证明 $C$ 为欧拉回路, 也即无向图 $G$ 为欧拉图. 假设 $C$ 不是欧拉回路, 设删去欧拉回路中的边后, 得到的新图为 $G‘ = (V, E‘)$ , 那么 $E‘$ 并非空集. 由于 $G$ 是连通图, 所以新图中至少存在一条边 $e \in E‘$ , 满足欧拉回路 $C$ 中的一个节点 $u$ 是 $e$ 的一端. 我们过边 $e$ 一定可以找到一条回路, 因为每个点的度数为偶数, 只有到度数为 0 , 即回到点 $u$ 才会停止. 我们发现, 可以把 $C$ 和新的回路进行合并, 进而说明 $C$ 不是最长的回路, 所以矛盾.
综上所述, 无向图 $G$ 中一定存在最长的回路 $C$ , 且 $C$ 就是欧拉回路.
与欧拉图类似的概念是半欧拉图, 我们根据定理1, 可以轻松地推广到无向半欧拉图判定定理.
定理2 (无向半欧拉图判定定理)
无向图 $G$ 为半欧拉图 $\Leftrightarrow$ $G$ 为连通图, 存在有且仅有两个点 $u, v$ 的度数为奇数, 其余点的度数为偶数.
证明
必要性显然, 下面证明充分性.
我们在 $u, v$ 间连接一条虚拟边, 构建新图 $G‘$ , 那么 $G‘$ 为连通图, 且所有点的度数为偶数. 根据定理1, 图 $G‘$ 一定存在欧拉回路 $C$ . 我们再将 $C$ 中的边 $(u, v)$ 去掉, 即可得到无向图 $G$ 的一条欧拉路径, 所以无向图 $G$ 为半欧拉图.
我们研究完了无向欧拉图的相关判定, 现在考虑研究有向图的相关判定.
照葫芦画瓢, 我们可以得到有向图的两个判定定理.
定理3 (有向欧拉图判定定理)
有向图 $G$ 为欧拉图 $\Leftrightarrow$ $G$ 的基图连通, 且所有点的入度与出度相等.
定理4 (有向半欧拉图判定定理)
有向图 $G$ 为半欧拉图 $\Leftrightarrow$ $G$ 的基图连通, 存在点 $u, v$ , $u$ 的入度比出度大 $1$ , $v$ 的入度比出度小 $1$ , 其余点的入度与出度相等.
最后考虑判定混合图是否是欧拉图.
大家可以参考这一篇博文: http://blog.csdn.net/commonc/article/details/52442882 .
混合图欧拉回路:
1. 如果基图不连通, 或者基图的某个点的度数不是偶数, 那么不可能是欧拉图.
2. 我们尝试将所有的无向边进行定向, 问是否存在某种方案, 使得每个点的入度与出度相同.
先将所有的无向边任意定向, 记每个点的入度与出度之差为 $d[1], d[2], ..., d[n]$ .
3. 建立源点 $S$ , 汇点 $T$ .
对于点 $i$ , 若 $d[i] > 0$ , 那么连边 $(i, T, \frac{d[i]}{2})$ .
对于点 $i$ , 若 $d[i] < 0$ , 那么连边 $(S, i, -\frac{d[i]}{2})$ .
对于定向的无向边 $(u, v)$ , 连边 $(u, v, 1)$ .
4. 跑网络流, 若没有满流, 则无解.
5. 把流满的边进行反向, 得到新图 $G‘$ , 对 $G‘$ 求欧拉回路.
$S$ 到 $T$ 的一条增广路的意义, 就是将路径上的所有边进行反向, 这样的影响是起点的出度-1, 入度+1, 终点的入度-1, 出度+1. 如果满流, 那么相当于完成了调整, 每个点的入度等于出度, 进而就有欧拉回路了.
最终, 混合图欧拉回路问题被转化为了有向图欧拉回路问题.
接下来, 考虑如何求出一条欧拉回路.
我们尝试 DFS 来找出欧拉回路, 并先观测一些小的情况.
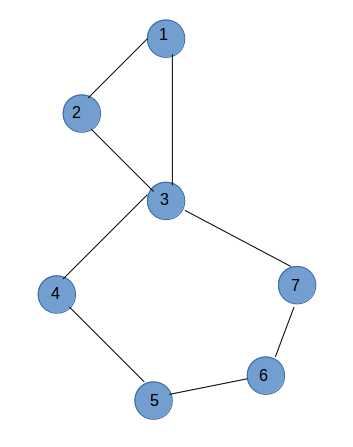
我们猜测可以从某个点开始 DFS , 贪心地选择每条边加入欧拉回路中?
不幸的是, 我们假如访问的顺序是 1 - 2 - 3 - 1 , 那么下面的环 3 - 4 - 5 - 6 - 7 - 3 就会被忽略掉.
这不要紧, 我们尝试列出完整的搜索序列: 1 - 2 - 3 - 1 - 4 - 5 - 6 - 7 - 3 . 我们发现, 虽然正着选取是不行的, 但是倒序得到的就是一个从点 3 开始出发的欧拉回路.
经过大量地实验, 我们可以猜测证明这是一个有生命力的一般性方法.
总之, 对于无向图, 我们的做法是: 从某个点开始 DFS , 访问没有访问的边, 将所有访问的边逆序加入 C 中, C 即为原图的欧拉回路.
那么, 对于有向图来说, 我们只需要对有向图的逆图执行上述算法即可.
标签:注意 ora comm 生命力 如图所示 png 网络 mon 混合图欧拉回路
原文地址:http://www.cnblogs.com/Sdchr/p/7533244.html