标签：算法   c++   数据结构   二叉树   

【注：相关概念来自经典教材、百度百科及维基百科】

树

树状图是一种数据结构，它是由n（n>=1）个有限节点组成一个具有层次关系的集合。它具有以下的特点：

• 每个节点（node）有零个或多个子节点；
• 没有父节点的节点称为根节点；
• 每一个非根节点有且只有一个父节点；
• 除了根节点外，每个子节点可以分为多个不相交的子树；

如图所示：

相关概念：

1. 节点的度：一个节点含有的子树的个数称为该节点的度；
2. 树的度：一棵树中，最大的节点的度称为树的度；
3. 叶节点或终端节点：度为零的节点；
4. 非终端节点或分支节点：度不为零的节点；
5. 父亲节点或父节点：若一个节点含有子节点，则这个节点称为其子节点的父节点；
6. 孩子节点或子节点：一个节点含有的子树的根节点称为该节点的子节点；
7. 兄弟节点：具有相同父节点的节点互称为兄弟节点；
8. 节点的层次：从根开始定义起，根为第1层，根的子节点为第2层，以此类推；
9. 树的高度或深度：树中节点的最大层次；
10. 堂兄弟节点：父节点在同一层的节点互为堂兄弟；
11. 节点的祖先：从根到该节点所经分支上的所有节点；
12. 子孙：以某节点为根的子树中任一节点都称为该节点的子孙。
13. 森林：由m（m>=0）棵互不相交的树的集合称为森林；

树的种类

• 无序树：树中任意节点的子节点之间没有顺序关系，这种树称为无序树，也称为自由树；【信息传播图】
• 有序树：树中任意节点的子节点之间有顺序关系，这种树称为有序树；【家族族谱图】
  • 二叉树：每个节点最多含有两个子树的树称为二叉树；
    • 完全二叉树：对于一颗二叉树，假设其深度为d（d>1）。除了第d层外，其它各层的节点数目均已达最大值，且第d层所有节点从左向右连续地紧密排列，这样的二叉树被称为完全二叉树；【倒数第一层不是倒数第二层的二倍，尚缺N个节点】
    • 满二叉树：对于上述的完全二叉树，如果去掉其第d层的所有节点，那么剩下的部分就构成一个满二叉树（此时该满二叉树的深度为d-1）；【倒数第一层是倒数第二层的二倍】
  • 霍夫曼树：带权路径最短的二叉树称为哈夫曼树或最优二叉树；【学过信息论的都知道霍夫曼编码，老NB了】
    
    
  • B树 【每一层数据大小有序】

二叉树

二叉树的每个结点至多只有二棵子树(不存在度大于2的结点)，二叉树的子树有左右之分，次序不能颠倒。二叉树的第i层至多有个结点；深度为k的二叉树至多有【用等比数列求和公式算算】个结点；对任何一棵二叉树T，如果其终端结点数为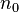，度为2的结点数为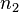，则。

树和二叉树的三个主要差别：

1. 树的结点个数至少为1，而二叉树的结点个数可以为0；
2. 树中结点的最大度数没有限制，而二叉树结点的最大度数为2；【度数即某节点的子节点个数】
3. 树的结点无左、右之分，而二叉树的结点有左、右之分。

访问二叉树

L、D、R分别表示遍历左子树、访问根结点和遍历右子树。那么根据排列组合，有6种可能。根据根的位置，常见以下三种遍历方法。先中后是相对根节点说的。注：一定程度上维基百科授人与鱼而不授人以渔，不能解惑。

前(先)序遍历

先(根)序遍历二叉树的顺序是DLR。【注意都是先L后R。】-----以下三张图片来源于课件

解释：每个节点都用DLR的顺序遍历。下同。

中序遍历

中(根)序遍历二叉树的顺序是LDR。【注意都是先L后R。】

后序遍历

后(根)序遍历二叉树的顺序是LRD。【注意都是先L后R。】

例子

例子来源于互联网及课件，分析为博主所写，如有错误，恳请指正。

例1：

先序遍历（根左右DLR）：ABDEC

中序遍历（左根右LDR）：DBEAC

后序遍历（左右根LRD）：DEBCA

例2：

先序遍历（根左右DLR）：ABCDEFGHK 【最简单的。先把根写下来，再写左子树的根，如果左子树还有子树，继续往下找，直到叶子节点！因为根左右，先写根，即遇到的就写下来！只需要注意同层的先写左，左如果有子树，继续遍历其子树。】

中序遍历（左根右LDR）：BDCAEHGKF 【不好写，容易犯错。从左子树开始寻找，子树里面还有子树，继续寻找其左子树，直到遇到叶子节点（D）或者没有左子树（B）写下来。例子里B没有左子树，所以先写，然后遍历右子树，右子树也从其左子树开始遍历，所以是BCD；相对根节点，左子树遍历完成，所以是BDCA；接下来遍历根节点的右子树，按上述步骤，既是：E（其没有左子树）H（叶子节点，其没有左子树，且是G的L）G（自身为根D）K（相对于节点G，其为R）G（G为F的L）F】

后序遍历（左右根LRD）：DCBHKGFEA 【先左子树，再右子树，最后根节点；没有左子树，则寻找此节点的右子树，在右子树里再按照LRD的顺序找，直到找到叶子节点（概念在上面），开始回溯写下来，相当于堆栈！】

例3：

怎么根据前序中序求后序：

已知前序遍历为GDAFEMHZ，中序遍历为ADEFGHMZ，请画出这棵二叉树。

①根据前序遍历特征，我们知道根结点必在首位置，所以为G；

②根据中序遍历特征。其中根节点G左侧的ADEF必然是根节点的左子树，G右侧的HMZ必然是根节点的右子树；

③根据前序中序特征，重复以上步骤。递归找到子树根节点；

那么，我们可以画出这个二叉树：

由图可知，后序遍历顺序为：AEFDHZMG

怎么根据后序中序求前序：

已知一棵二叉树的中序序列和后序序列分别是BDCEAFHG 和 DECBHGFA，请画出这棵二叉树。
分析：
①由后序遍历特征，根结点必在后序序列尾部（即A）；
②由中序遍历特征，根结点必在其中间，而且其左部必全部是左子树的子孙（即BDCE），其右部必全部是右子树的子孙（即FHG）；
③递归找出子树根节点。
那么，我们可以画出这个二叉树：

注意事项：

    左子树中序为BDCE，后序为DECB，说明B为A的左子树根节点，C为B的右子树（从BDCE看出）根节点（从DCE及DEC看出）；

    右子树中序为FHG，后序为HGF，说明F为A的右子树的根节点，H为G的左子树根节点。

C++实现

反爬虫，先不写了。

本文由@The_Third_Wave（Blog地址：http://blog.csdn.net/zhanh1218）原创。还有未涉及的，会不定期更新，有错误请指正。

如果你看到这篇博文时发现不完整，那是我为防止爬虫先发布一半的原因，请看原作者Blog。

如果这篇博文对您有帮助，为了好的网络环境，不建议转载，建议收藏！如果您一定要转载，请带上后缀和本文地址。

树和二叉树总结及算法实现

标签：算法   c++   数据结构   二叉树   

原文地址：http://blog.csdn.net/zhanh1218/article/details/39123975