标签:解决 std def str add 答案 ima tor space
屯一个虚树的板子,顺便总结一下这样的题型。
给定一棵n个节点的有根树,在输入数据通过给出每个节点的父亲来表示这棵树。若某个节点的父亲为0,那么该节点即为根。现在对于每个点,询问它的每个祖先的所有深度不超过该节点的儿子的数量的总和。
第一行一个整数n。第二行n个整数,表示每个节点的父亲pi。
输出一行n个整数,表示每个节点的答案。
5
2 3 4 5 0
10 6 3 1 0
1<= n <=5*10^5,0<= pi <= n,保证有且仅有一个pi = 0。
这道题的思路是显而易见的。
对于每个节点,它的贡献是它到根的一条链(给它的所有祖先的子树大小+1)。
每个节点的询问也是它到根的那一条链。
至于深度不超过询问节点,我们发现,对于每个节点,只有深度小等于它的节点才对它有贡献,而且是一定有贡献。
所以我们把所有点按深度排序,一层一层地做。插入一层,询问一层。
用上树链剖分你就会在O(nlog2n)的时间内T掉该题。(如果你用树剖过了当我没说)
然后我们考虑怎么将它优化。
对于修改链的问题,我们通常可以通过逆向思考,将其变为子树修改,复杂度可以从O(nlog2n)降为O(nlogn)。
询问很显然是很容易转化的,每个点都询问它的所有祖先,相当于每个点都对它的所有子节点加上答案贡献。
而对于修改我们则要分析一下:
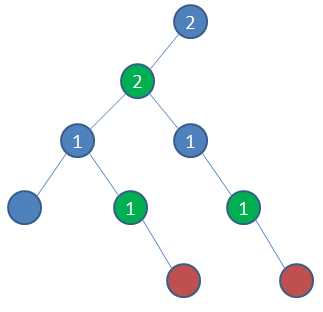
如图,我们做到了第5层,计算红色节点对祖先子树大小的贡献。
我们发现两个节点的贡献会在他们的lca处合并,那么这样一来正好构成一棵以该深度的点为叶节点的虚树!(即绿色节点)
虚树上每个节点x到它父亲的这条链上被红色节点的贡献val[x]都是相等的,
因此虚树上每个节点x对该节点的子节点们的贡献就是val[x]*(dep[x]-dep[fa[x]])!
虚树的点数和叶节点数同级,所以总复杂度为O(nlogn)。
然而通过观察,我们还可以发现每一层的节点答案对下一层是具有递推关系的。
一个结点的答案可以由它父亲的答案加上该节点所在层的所有节点对它的贡献,这个我们同样可以用虚树解决。
搞出虚树上每个节点被红色节点的贡献,然后从虚树根出发,往下dfs,到底层节点就计算一下答案即可。
如果你用上tarjan求lca和一些骚排序(如果你愿意的话)可以把时间复杂度优化到O(n)。(你大可把这句话当成是小C在口胡)
代码是第二种做法:
#include <cstdio> #include <cstring> #include <algorithm> #include <vector> #define ll long long #define MN 500005 #define MS 20 using namespace std; struct edge{int nex,to;}e[MN]; int dfbg[MN],dfed[MN],dep[MN],hr[MN],q[MN],siz[MN],fa[MS][MN],b[MN],u[MN]; ll t[MN],ans[MN]; vector <int> d[MN]; int dfn,pin,bin,tp,n,rt; inline int read() { int n=0,f=1; char c=getchar(); while (c<‘0‘ || c>‘9‘) {if(c==‘-‘)f=-1; c=getchar();} while (c>=‘0‘ && c<=‘9‘) {n=n*10+c-‘0‘; c=getchar();} return n*f; } inline void ins(int x,int y) {e[++pin]=(edge){hr[x],y}; hr[x]=pin;} void dfs(int x,int depth) { dfbg[x]=++dfn; dep[x]=depth; d[depth].push_back(x); for (register int i=hr[x];i;i=e[i].nex) dfs(e[i].to,depth+1); dfed[x]=dfn; } int lca(int x,int y) { register int i,k; if (dep[x]<dep[y]) swap(x,y); for (k=dep[x]-dep[y],i=0;k;k>>=1,++i) if (k&1) x=fa[i][x]; if (x==y) return x; for (i=MS-1;i>=0;--i) if (fa[i][x]!=fa[i][y]) x=fa[i][x],y=fa[i][y]; return fa[0][x]; } inline void pushs(int x) {while (tp&&dfbg[x]>dfed[q[tp]]) --tp; if (tp) ins(q[tp],x); q[++tp]=x;} inline int lowbit(int x) {return x&-x;} inline void getadd(int x,int z) {for (;x<=n;x+=lowbit(x)) t[x]+=z;} inline ll getsum(int x) {ll lt=0; for (;x;x-=lowbit(x)) lt+=t[x]; return lt;} void dp(int x,int fat) { siz[x]=u[x]; for (register int i=hr[x];i;i=e[i].nex) dp(e[i].to,x),siz[x]+=siz[e[i].to]; getadd(dfbg[x]+1, 1LL*siz[x]*(dep[x]-dep[fat])); getadd(dfed[x]+1,-1LL*siz[x]*(dep[x]-dep[fat])); } bool cmp(int x,int y) {return dfbg[x]<dfbg[y];} int main() { register int i,j; n=read(); bin=0; for (i=1;i<=n;++i) ins(fa[0][i]=read(),i),b[++bin]=i; for (i=1;i<=n;++i) if (!fa[0][i]) rt=i; for (i=1;i<MS;++i) for (j=1;j<=n;++j) fa[i][j]=fa[i-1][fa[i-1][j]]; dfs(rt,1); for (i=2;d[i].size();++i) { for (j=1;j<=bin;++j) hr[b[j]]=u[b[j]]=0; tp=pin=bin=0; for (j=0;j<d[i].size();++j) ++u[b[++bin]=fa[0][d[i][j]]]; bin=unique(b+1,b+bin+1)-b-1; for (j=1;j<bin;++j) b[bin+j]=lca(b[j],b[j+1]); bin=bin*2-1; sort(b+1,b+bin+1,cmp); bin=unique(b+1,b+bin+1)-b-1; for (j=1;j<=bin;++j) pushs(b[j]); dp(q[1],0); for (j=0;j<d[i].size();++j) ans[d[i][j]]=getsum(dfbg[d[i][j]]); } for (i=1;i<=n;++i) printf("%I64d ",ans[i]); }
感觉全程打得最难受的是倍增求lca,小C一直觉得自己的lca写得奇丑无比。
[Codeforces]860E Arkady and a Nobody-men
标签:解决 std def str add 答案 ima tor space
原文地址:http://www.cnblogs.com/ACMLCZH/p/7551440.html