标签:style blog http os io ar for 2014 sp
题目大意:总共有n个节点,其中有发电站np个、用户nc个和调度器n-np-nc个三种节点,每个发电站有一个最大发电量,每个用户有个最大接受电量,现在有m条有向边,边有一个最大的流量代表,最多可以流出这么多电,现在从发电站发电到用户,问最多可以发多少电
解题思路:将发电站看成源点,用户看成汇点,这样求最大流就可以了,不过因为有多个源点和汇点,所以加一个超级源点指向所有的发电站,流量总量为发电站的流量总量,加一个超级汇点让所有的用户指向他,流量为用户的最大流量,这样,从超级源点到超级汇点求最大流即可。
关于dinic算法:EdmondsKarp在BFS之后从终点开始按照pre域进行递减,dinic在BFS之后从源点进行递归。
层次图是什么东西呢?层次,其实就是从源点走到那个点的最短路径长度。其实EdmondsKarp也是按照层次来获得最短路的,算法导论在证明按照最短路寻找增广路时,假设所有边权值为1.
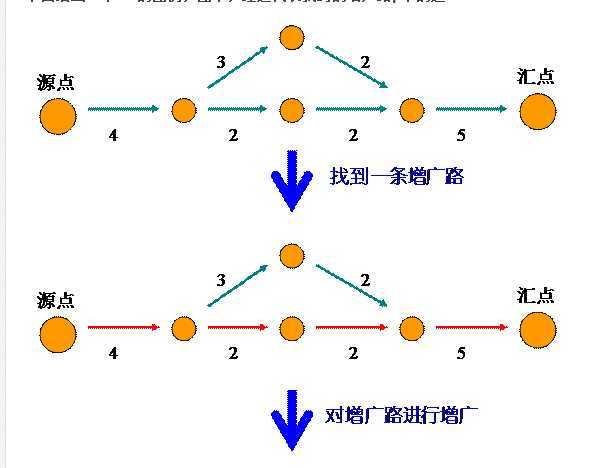
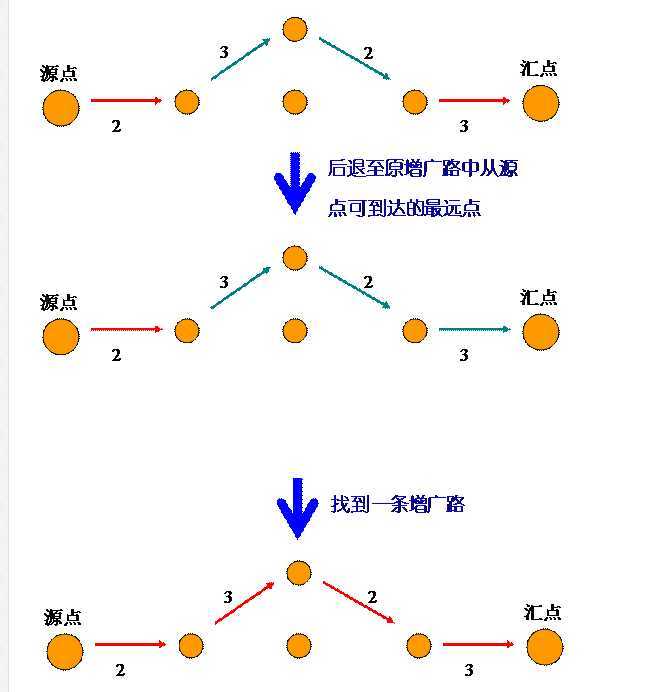
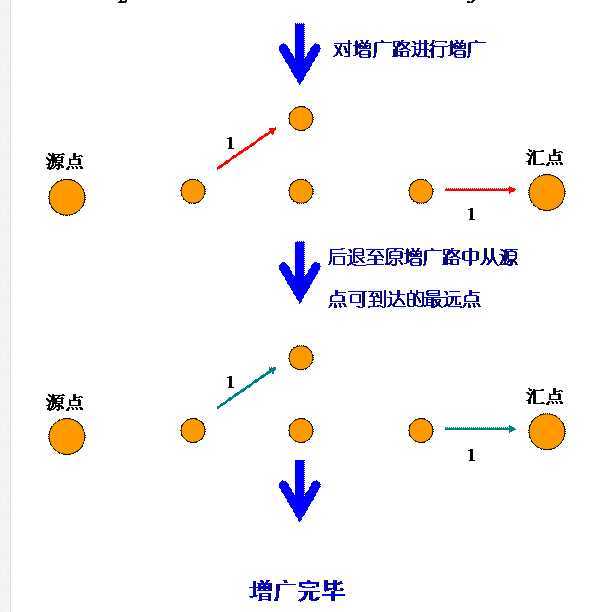
这样的话,在找到第一条增广路径后,只需要回溯到 b 点,就可以继续找下去了。
这样做的好处是,避免了找到一条路径就从头开始寻找另外一条的开销。
也就是再次从 S 寻找到 b 的开销。
这个过程看似复杂,但是代码实现起来很优雅,因为它的本质就是回溯!
下面给出一个dfs的图例,图中,红边代表找到的增广路p中的边。
/*
dinic
Memory 320K
Time 563MS
*/
#include <iostream>
#include <queue>
using namespace std;
#define min(a,b) (a<b?a:b)
#define MAXV 105
#define MAXINT INT_MAX
typedef struct{
int flow; //流量
int capacity; //最大容量值
}maps;
maps map[MAXV][MAXV];
int dis[MAXV]; //用于dinic分层
int vertime; //顶点总数
int nedges; //边的总数
int power_stations; //发电站总数
int consumers; //消费者总数
int maxflow; //最大流
int sp,fp; //标记源点与汇点
bool bfs(){
int v,i;
queue <int>q;
memset(dis,0,sizeof(dis));
q.push(sp);
dis[sp]=1;
while(!q.empty()){
v=q.front();q.pop();
for(i=1;i<=vertime;i++)
if(!dis[i] && map[v][i].capacity>map[v][i].flow){
q.push(i);
dis[i]=dis[v]+1;
}
if(v==fp) return 1;//仍然能找到增广路,返回1
}
return 0;//遍历完所有节点,仍然没有fp,说明找不到增广路了
}
int dfs(int cur,int cp){
if(cur==fp) return cp;//如果访问到汇点,则结束。必须要找到汇点,即找到一条完整的增广路后才进行增广路的权值减少。如果找不到,直接return cp-tmp;从而处理该层节点的上一层节点。
int tmp=cp,t;
for(int i=1;i<=vertime;i++)
if(dis[i]==dis[cur]+1 && tmp && map[cur][i].capacity>map[cur][i].flow){
t=dfs(i,min(map[cur][i].capacity-map[cur][i].flow,tmp));
//由于我们最终需要得到最短增广路上的最小残留量,因此我们在判断一个新访问边是否为最小的同时,必须考虑前面的边是否更小,这里的参数cp作用就是表示前面已经访问的边最小值。起始时,temp为无限大,被map[sp][i].capacity-map[sp][i].flow替换,以后DFS中,已经被访问边的最小值(即cp)要与当前边进行比较。
当所有的DFS结束后,才能获得最终的t值,从栈顶逐渐把各个边加上这个增广路的最小权值
注意if之后的括号一直到temp-=t,必须满足边的要求才可以减边
map[cur][i].flow+=t;
map[i][cur].flow-=t;
tmp-=t;}
//之所以比匈牙利速度快,就在于这里不是找到一条增广路就直接退出了,而是在当前边减去t之后,继续for循环,在当前边减去之后,继续下一个可能的增广路。为了防止前面路径可能不够减的情况,特意将temp-t表示前面所有路径最短的在减去t的情况下,同时保证temp>0(for循环的条件),寻找下一个完整的增广路。
//n个点,m个边,总复杂度为O(m*n^2),一次dfs的复杂度为O(m*n),dfs次数为n次
对于dinic是不会出现匈牙利算法中出现的:边(i,j)被消除以后,又被反向地出现在增广路上,即边(i,j)变成(j,i),因为i,j是有层数关系的,必须由i到j,而不是反过来。因此在dfs中,找到一个增广路并且减去最小权值边后,该边就不再出现(一次BFS里,节点的dis值是确定的、不会被再次修改的,因此不可能返回)。因此共有m个增广路,找一条增广路的时间为n,至于为什么,需要看平摊分析(我的理解是:第一次找增广路需要遍历所有可能性,以后的增广路只需要在第一个基础上搜索即可),看下面:
我们现在来证每次搜索一条增广路的复杂度平摊是O(n)。
搜索有三种类别:1.前进,2.后退,3.无效枚举。
前进必然会搜到一个“新”的点,“后退”会删掉一个“肯定无用”的点,那么前进和后退的总时间复杂度为O(n),无效枚举是指枚举到了一个已经被标记“无用”的点,而我们发现,对一条边(i,j)来说,j最多只会被i无效枚举1次,为什么呢?因为如果j被i枚举了两次,说明i已经被“后退”了一次,说明i已经被删掉了,所以不可能在回来!因此每条边最多只会无效枚举1次。因为在m次搜索中,无效枚举的总次数是m,可以忽略。
因为最多进行n次dfs,(因为对于从源点到与其直接相连的点(假设为j),在更新i到j到终点的增广路后,j点已经不再与终点有通路,必须换一个点,最多n-1个点都与源点相连,并且可以连接到终点)
所以在Dinic算法中找增广路的总复杂度为O(m*n^2) ,这也是Dinic算法的总复杂度。
return cp-tmp;//表示增广路上前面节点都必须减去的权值量。这里不能简单return t,因为temp不止要减一次t。
}
void dinic(){
maxflow=0;
while(bfs()) maxflow+=dfs(sp,MAXINT);//maxint为无限大。
}
int main(){
int i;
int x,y,z;
char ch;
while(scanf("%d%d%d%d", &vertime, &power_stations,&consumers,&nedges)!= EOF){
//Init
memset(map,0,sizeof(map));
//Read Gragh
for(i=1;i<=nedges;i++){ //设置读图从1开始
cin>>ch>>x>>ch>>y>>ch>>z;
map[x+1][y+1].capacity=z;
}
//Build Gragh
//建立超级源点指向所有的发电站,流量为有限值
sp=vertime+1;fp=vertime+2;vertime+=2;
for (i=1; i<=power_stations; i++){
cin>>ch>>x>>ch>>y;
map[sp][x+1].capacity=y;
}
//建立超级汇点,使所有消费者指向它
for (i=1; i<=consumers; i++){
cin>>ch>>x>>ch>>y;
map[x+1][fp].capacity=y;
}
dinic();
printf("%d\n",maxflow);
}
return 0;
}
标签:style blog http os io ar for 2014 sp
原文地址:http://www.cnblogs.com/notlate/p/3962208.html