标签:加速度 size 变换 选择 解释 整理 文学 数学 重点
近期,六岁的女儿在学钢琴,作为监工和陪练,这对我却是个不大不小的困难。因为陪练并不是站在一旁嚷嚷着“好好练琴”就行,共同学习、一起交流才能够让小孩有持续的热情。为了把这件事变得有趣和高效,我打算从零学一点音乐,首先至少能看懂少儿钢琴的书吧。想想我们这一代的农村学校,连个音乐老师都没有,更不谈什么音乐知识,能接受到的音乐“熏陶”恐怕也只有大街小巷的那些流行歌曲了。这种粗粝的音乐审美也许已经无法提高,但“学习基础乐理”这样的硬任务应该还是可以完成的。
很久之前就听说音乐和数学有着千丝万缕的联系,我早就想一睹音乐中的数学之美,但拿起各种正规乐理教材后,心里的落差还是很大的。不仅没有数学教材的那种干净利落,甚至也没有计算机教材的循序渐进,整个就是杂乱概念的堆砌。概念没有清晰的定义、没有引入的原因,概念间复杂的关系更是说不清楚道不明,名词总是硬生生地放在那里,你记就是了。也许是因为多年的理工科工作习惯,这样的书我真是一页也看不下去,不是看不懂,而是看得不得劲。但静下心来想想,我需要的只是对概念来源的一个解释,哪怕是一个错误的解释,只要我觉得合理就行。
当然我也知道,音乐本身还是感性的东西,它变换莫测、风格多变,甚至连好坏都没有统一的标准,想用一套理论就把它完全解释肯定是不现实的。但万事万物都都会有一些基本规律存在,人类文明也正是在归纳总结中积累起来的,即使是艺术、文学类的创作,也都要满足基本的美学规律。音乐作为一个普世的文化活动,经过上千年的流传和演进,在不同地域的文明中都建立起了理论体系。但令人惊奇是,在音律的基本要素上,各种体系都殊路同归,具有非常类似的构成。如今,音律的语言已经趋于一致,人们已经有了统一的描述方式,并且在此之上继续探索、总结……
音律中跟数学关系最直接、最久远的当属音阶系统了,早在古希腊时期,毕达哥拉斯学派就发现,频率呈简单整数比的两个音听起来非常协和,并且几乎全世界的音阶系统,都是基于这样一个简单的事实建立起来的。下面开始,我就试图用自己浅薄的数学知识来解释一下这套体系,当然其中以数学的阐述为主,而有意淡化乐理的琐碎概念和乐谱的基本知识,那些在任何一本乐理书上都有详尽的介绍。最后我还想说,对于乐器演奏技法、甚至音乐理论学习,整理这些东西并无大用,用这种思维去学习音乐也必将学无所成。但对于一个理科生,只是想要一个解释而已,这不算过分吧,先让我痛快了再说!

首先严格说,声音就是一段声波,它是物体震动从而带动的空气震动。当然,杂乱无章的震动并不能对听觉提供可识别的特征信息,具有明显特征的声音在一段时间内应当(或近似)呈现一定的周期性,所谓周期性就是震动以一定频率重复出现。有三个特征可以完整刻画一段周期声波,首先是声波的震动周期,它一般用频率来表示,在音乐里还叫音高,人耳能听到的声音频率大概是\(20\sim 20000Hz\)。第二个是声波的形状,它构成了每段声音的独特感觉,音乐上也叫音色,不同乐器发出的声音都很容易辨认,就是因为它们的音色不同。第三个就是声音震动幅度的大小,它直接关系到声音的大小,也就是我们平常说的音量。
教材上还告诉我们,每个周期声波都是有一系列频率为\(f,2f,3f,\cdots\)的正弦波(振幅不同)叠加而成的。但我觉得这个说法并不严谨,虽然傅里叶级数告诉我们:“满足一定条件的周期函数可以有唯一的傅里叶分解”,但这并不能说明:周期声波天然地就是由那些正弦波叠加而成的。傅里叶级数只是数学工具,它是个人工概念,用来帮助人们分解声音以便更好的分析。就好比物理上经常把运动按正交轴进行分解一样,这是用数学工具来分析运动,但并不是说:运动天然地就是由两个方向的运动组成。
正弦波也叫简谐波,它是由简谐振动产生的声波,而简谐振动现实中非常普遍的一种运动。所谓简谐振动可以这样描述:它在中心两侧运动,加速度(或所受合力)始终指向中心,并与位移\(y\)成正比。弹簧的震动就是典型的简谐振动,其实现实中大部分物体的自身震动都是由若干简谐振动组成的,这也说明了为什么周期声波都可以很好地进行傅里叶分解。在音乐里,简谐波也叫纯音,纯音叠加而成的复合音,如果仍然有明显的周期,则叫单音,否则叫拍音。单音的傅里叶分解中,周期最大的纯音叫做这个单音的基音,其它纯音则叫泛音。
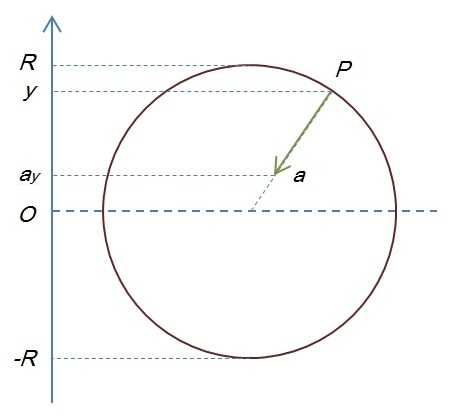
到这里还有最后一个问题:为什么简谐波就是正(余)弦波,仅仅因为它好看吗?我只得承认,书本里学的知识已经全部忘记了,现在只好自己再推算一遍。一种直接的方法就是根据简谐振动的特点,可以得到式(1)的常微分方程,从而解得\(y(t)\)是正弦函数。还有一种间接的证明方法,就是观察如图的匀速圆周运动。考察运动点\(P\)以及其加速度\(a\)在\(y\)轴的投影,显然它们成正比关系,具体说就是\(a_y(t)=\dfrac{a}{R}y(t)\)。也就是说简谐振动正是匀速圆周运动在一维空间的投影,设它的角速度是\(\omega\)(逆时针方向),它的波形自然就是\(R\sin\,\omega t\)。
\[y‘‘(t)=ky(t)\tag{1}\]
单丝不成线,单音不成乐,一首动听的音乐当然要有不同音高的单音,才能表达出情绪的波动。我们也看到,任何一种乐器都能发出多种音高,它们交叉、重叠、依次推进,形成了非常有节奏的韵律。为了能用不同的乐器、在不同的时间和场所弹奏同样一首曲子,需要对每个音作明确定义,这就要事先选定一组单音做为标准,这个组合也被称为音阶。每种乐器使用的音阶不尽相同,但挑选时都遵循着类似的准则,这里我们先跳过漫长的历史过程,来看看如何合理地构建一个通用的音阶。
首先我们知道一个常识:人耳对音高的感知满足对数函数,也就是说音高分别为\(F_a,F_b\)的声音,我们感觉到的“声高”比(我捏造的词)则是\(\dfrac{L_a}{L_b}=\dfrac{\ln F_a}{\ln F_b}\)。设音阶中单音的声高和音高分别是\(L_i,F_i\),则容易有关系式(2)成立(\(C\)为某常数)。另外,我们希望音阶里的“声高”是逐渐递增的,也就是说\(L_1,L_2,\cdots,L_n\)成等差数列。由式(2)易知\(L_a-L_b=C\ln F_a/F_b\),从而\(F_1,F_2,\cdots,F_n\)成等比数列。
\[\dfrac{L_1}{\ln F_1}=\dfrac{L_2}{\ln F_2}=\cdots=\dfrac{L_n}{\ln F_n}\;\Rightarrow\;L_i=C\ln F_i\tag{2}\]
把音阶设计成等比数列有很多好处,首先是得到了一套完整、递进的声高系统,它能满足各种场合的需求。还有就是等比音高可以很方便地“转调”,所谓转调就是把乐曲中的每个音都同时升高或降低相同的声高,下面的调式中会碰到这样的情况。总之这是一个不错的开始,只要再添加少许限制,就可以确定这套音阶了。音乐中的不同单音扮演着不同的角色,它们需要配合使用才能体现出流畅或变化,所谓流畅就是两个单音出现重合或叠加时,并不显得突兀,而是显得十分“协和”。
早在古希腊时期人们就发现,频率成简单整数比的两个音在一起更加协和,尤其是成倍数关系的两个音叠加时,音高并没有变化。这个其实不难解释,两个周期比为\(m:n\)的两个音重合时,周期变为最小公倍数\([m,n]\),当\(m,n\)都不大时,重合音的音高也没有突然降低,并且都是原来音高的倍数。既然倍数关系的音高是最协和的,我们就必须把最简单的倍数\(2:1\)添加到音阶中,任意选定一个“基础音”后,它的\(2^k,2^{-k}\)倍音也必须出现在音阶中,这就得到了音阶序列\(\cdots,\,2^{-2}F,\,2^{-1}F,\,F,\,2F,\,2^2F,\,\cdots\)。
但是成倍数的单音又太过协和了,完全体现不出变化,乐曲会显得很空洞。所以需要在\([F,2F]\)间再添加一些音(其它区间类似),当然添加不能忘了等比关系,添加后的音应当是式(3)的序列。这时只要确定整数\(n\)即可,而这只需再添加一个音。所有非倍数的整数比中最简单的就是\(2:3\),从而把\(\dfrac{3}{2}F\)添加进序列(3)是毫无争议的,也就是寻找\(m\)使得\(2^{\frac{m}{n}}=\dfrac{3}{2}\)。
\[2^0F=F,\:2^{\frac{1}{n}}F,\:2^{\frac{2}{n}}F,\:\cdots,\:2^{\frac{n-1}{n}}F,\:2^{\frac{n}{n}}F=2F\tag{3}\]
但显然\(\log_2\dfrac{3}{2}=0.5849625\cdots\)是无理数,不能表示成\(\dfrac{m}{n}\)的形式,这时我们只能稍作妥协,取一个\(\log_2\dfrac{3}{2}\)的近似分数。到了这一步,自然地就想到了实数的连分数表示,首先算得\(\log_2\dfrac{3}{2}\)的简单连分数是\([1,1,2,2,3,1,5,2,23,\cdots]\),前几个近似分数分别是\(1,\dfrac{1}{2},\dfrac{3}{5},\dfrac{7}{12},\dfrac{24}{41},\dfrac{31}{53},\cdots\)。第一个达到\(0.1%%\)精度的(包括第一类近似逼近)是\(\dfrac{7}{12}\),\(12\)大小合适,并且在古代是个很有地位的数(因为约数多),不选它简直天理难容了。
\[\log_2\dfrac{3}{2}=\cfrac{1}{1+\cfrac{1}{1+\cfrac{1}{2+\cfrac{1}{2+\cdots}}}}\approx\dfrac{7}{12}\tag{4}\]
以此建立音阶的方法就叫做十二平均律,它诞生于相当久远的中国古代,16世纪由明朝的朱载堉发展成完整的理论,然后在16世纪末传播到欧洲并在17世纪得以普及。十二平均律是目前通用的音律体系,后面的音程、调式、调性、和声、和弦理论都是建立在此之上的,只不过这些理论几乎都是在欧洲发展起来的。
在音律中有时非常关心两个单音之间的“距离”,它显然可以用单音的频率比来度量,这个比率在音乐中也被叫做音程。由于十二平均律得到音阶形成完整的等比数列,从而可以用相邻单音的频率比作为单位来“数”出音程大小,这个单位叫做一个“半音”,两个半音则叫一个“全音”,这样的音程表示法也叫音数。至于为什么把半音作为一个单位,我想大概是因为许多音阶中,两个半音的距离是比较主要的音程,这个在下面的调式中将详细讨论。另外,一个半音还被分为100个音分,它可以用来度量更小精度的音程。
由于\(F\)与\(2F\)的单音极度相似,音阶中就好像只有12个音循环出现(只是音高加倍),因此我们把讨论的重点放在一个周期中。在正式给出这些音的名称之前,这里先用数字\(0\sim 12\)代表它们,下面要讨论的是这13个单音之间的协和程度。这属于乐理中的和声学部分,那里把音程的协和程度分成了五种:极完全协和、完全协和、不完全协和、不协和、极不协和。首先我们知道,音\(0\)与音\(12\)以及自身是非常协和的,它们也叫做极完全协和音程。
然后我们还知道,音\(0\)与音\(7\)的频率比近似为\(2:3\),它们的协和程度也很高,从而被叫做完全协和音程。接下来,音\(7\)的\(\dfrac{3}{2}\)倍音出现在了下一个循环中,熟知取模运算的你一定知道,它就是音\(2\)的2倍音。从而易知音\(2\)与音\(7\)的近似频率比为\(\dfrac{4}{3}\),它们也是完全协和的。换句话说,任何一个音都有上下两个与它完全协和的音,这个协和关系可以像下图那样形成一个环链(因为7与12互质)。
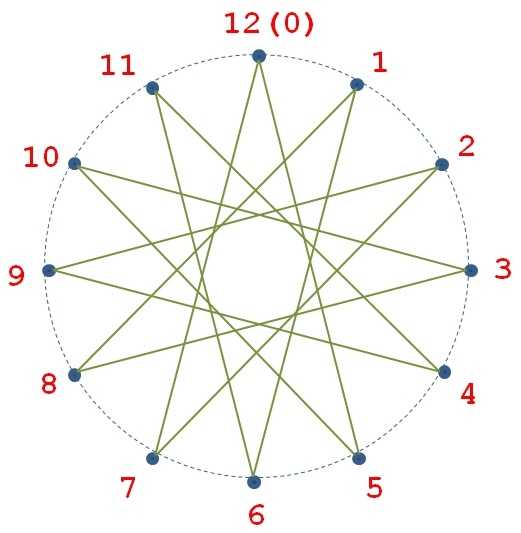
历史上,早期的音阶其实就是用上图的环链构建的,但只是使用了环中的\(5\)-\(0\)-\(7\)-\(2\)-\(9\)-\(4\)-\(11\)一段共七个音。由于音程\(\dfrac{3}{2}\)也叫纯五度(下面再介绍),故这个方法也叫五度相生律。但不难发现,五度相生律中会出现分母很大的分数,崇尚小整数比的古人利用小质数\(2,3,5\)构建出了它们的近似分数(见下表,不包括括号内的音),这个生成法也叫纯率。五度相生律更注重单音之间的协和性,而纯率更关注所有单音与\(F\)之间的协和性,在无法协调的情况下,十二平均律则是一个折中的方法。并且十二平均律的平滑性和完整性,也使得它成为了后来的标准。五度相生律和纯率被长期使用的期间,七个音的音名也被约定俗成地继承了下来(见下表,括号中是它们的唱名),后来添加进来的五个音只好用升降号来表示。
| 十二平均律 | 五度相生律 | 纯率 | 音名(唱名) | 音程 |
| \(1\) | \(1\) | \(1\) | C (Do) | 纯一度 |
| \(2^\frac{1}{12}\) | \((256/243)\) | \((17/16)\) | C# / Db | 小二度 |
| \(2^\frac{2}{12}\) | \(9/8\) | \(9/8\) | D (Re) | 大二度 |
| \(2^\frac{3}{12}\) | \((32/27)\) | \((6/5)\) | D# / Eb | 小三度 |
| \(2^\frac{4}{12}\) | \(81/64\) | \(5/4\) | E (Mi) | 大三度 |
| \(2^\frac{5}{12}\) | \(4/3\) | \(4/3\) | F (Fa) | 纯四度 |
| \(2^\frac{6}{12}\) | \((729/512)\) | \((7/5)\) | F# / Gb | 增四 / 减五 |
| \(2^\frac{7}{12}\) | \(3/2\) | \(3/2\) | G (So) | 纯五度 |
| \(2^\frac{8}{12}\) | \((128/81)\) | \((8/5)\) | G# / Ab | 小六度 |
| \(2^\frac{9}{12}\) | \(27/16\) | \(5/3\) | A (La) | 大六度 |
| \(2^\frac{10}{12}\) | \((16/9)\) | \((9/5)\) | A# / Bb | 小七度 |
| \(2^\frac{11}{12}\) | \(243/64\) | \(17/8\) | B (Si) | 大七度 |
| \(2\) | \(2\) | \(2\) | C (Do) | 纯八度 |
伴随着七个单音,音程也有对应的名字,单音到自身的音程叫一度,然后依次增一度,到2倍音程叫八度。可见度数并不是严格的定义,而是一个经验性的命名,从我有限的资料中并未找到它的来源,以下纯属瞎掰。由于一度、四度、五度、八度有很强的协和性和确定的频率,它们也被叫做纯音。二、三、六、七度前面都补充了一个降半音的音,为区别开来,把原来的四个叫大X度,新增的叫小X度。这十三个度数之间近似相差半个音,之所以说近似,是因为非平均律下,这个间距就不是半个音了。所以当一个音要增、减半个音(一个音)时,还特地取名为增、减音程(倍增、减音程),下表总结了音程名称的变化规律,左右相邻的两个音程相差半个音。
| 倍减音程 | 减音程 | 纯音程 | 增音程 | 倍增音程 | |
| 小音程 | 大音程 | ||||
关于其它音程的协和性,一般把三度、六度看成是不完全协和的,大二、小七看成是不协和的,小二、大七看成是极不协和的,增四/减五则表现极不稳定。其原因一般也归结为整数比的“复杂”程度,但如何定义这个复杂程度则莫衷一是,各种解释都不能让人信服。如果小整数比的理论成立,那这些协和性很可能只对纯律有效。在十二平均律下,每个频率都有许多近似分数,如何选择代表分数是个难题,以下只是我的推测。
对于音程为\(x>1\)的两个音,设周期分别为\(T,xT\),它们的和声不一定有固定周期,只有一些大大小小的近似周期。一个近似周期应当同时约等于\(T,xT\)的倍数,设它们是\(mT,nxT\),要想周期比较明显,\(|m-nx|T\)应当足够小。最小的近似周期应当满足:\(m,n\)尽量小而\(|m-nx|\)也能足够小,回顾连分数的知识可知,这等价于求实数\(x\)的第二类最佳逼近\(\dfrac{m}{n}\)。纯率选取的分数其实就是达到一定精度的第二类逼近,然后\(n\)越小的协和性越好,这与感觉基本吻合。另外我还有一个猜想,那种有理逼近比较慢的音程,由于近似精度低且两个近似周期之间相差小,和声会显得不协和或不稳定。比如典型的增四/减五音,它的连分数是\([1;2,2,2,2,2\cdots]\),由于连分数的逼近速度慢,它的和声就很不稳定。
以上是关于音阶的基础理论,在实际的曲调中往往只选取少量的音组成音阶,并且在不同时代、不同地区形成了各种风格的音阶。这里讲的“风格”其实就是音阶的“调”,它关系到音乐的情感色彩和情绪高低。一个调(音阶)包括选定的主音以及其它音的音程,它们分别称为调性和调式。
先来看调式,它是指围绕某个主音(Ⅰ)而生成的音阶,对于一种调式,其它音的个数以及相对主音的音程是确定的。在不同的历史时期和地区,产生了风格迥异的调式,这里只拿自然大(小)调为例,介绍调式的构成。自然大(小)调就是我们熟悉的七音音阶,除了主音外先加入上下五度的两个音:属音(V)和下属音(Ⅳ),然后是位于主音、属音中间的中音(Ⅲ)和位于主音(高八度)、下属音中间的下中音(Ⅵ),最后再加上与主音相邻的上主音(Ⅱ)和下主音(Ⅶ)(小调中叫导音)。一般来说,自然大调表现出阳光明朗的风格,而自然小调则阴暗忧伤一点。
在具体音程上,首先两个属音的位置没有疑问,以纯五度为准。但主音和属音之间相差\(3.5\)个半音,中音的位置有两种选择,自然大调选择\(2+1.5\)方式,而自然小调选择\(1.5+2\)的方式,这种不同继而还会影响上(下)主音的位置。最终,自然大调的音程从主音开始依次是“全全半全全全半”,而自然小调则是“全半全全半全全”。如果把音程放到一个八度闭环中,不难发现大、小调其实是“同构”的,只不过平展后有些音相差八度而已。

调性比较简单,主音是什么,一般就叫什么调,比如C调、G调。由于在平均律中有同音异名的现象,同一个调可能有两个名字,比如F#调和Gb调就是相同的。但在非平均律下,它们会有细微的差别,这个我们不多讨论。还有一个问题我们一直没有解决,就是这些音的频率究竟是多少?历史上,标准音的标准一直在变,直到1936年,美国标准委员会才将小字一组的A音(a1)定为440Hz,而与它同一组的C音称为中央C。
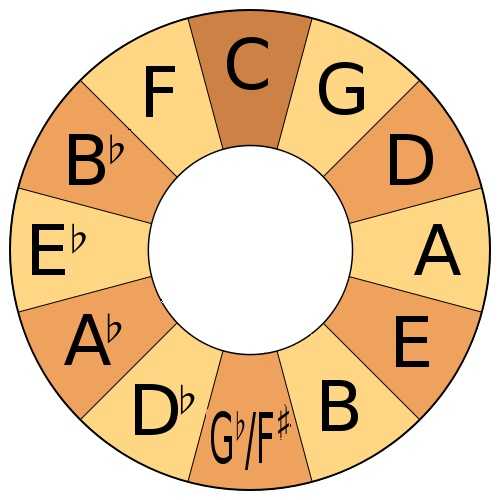
有了调式和调性后,音乐的调也就确定了,比如C大调、A小调等。下图将12个音按照五度音程串成一个圆环,由前面的讨论可知,圆环中任何7个相邻的音都正好构成一个自然大(小)调。7个相邻音中的(顺时针)第2个是大调的调性音,而第4个则是小调的调性音,利用这个图可以快速确定不同的音调。至此,我们就算整理完音阶中的数学解释了,但对于乐理知识,这些只能算开篇和序言,希望我这种另类的开篇可以帮助到你。
博客总目录在这里
【前序学科】 实数系统(连分数)
【参考资料】
[1] 《写给理工科看的乐理》,博客园Devymex
[2] 知乎: www.zhihu.com/question/20612595; www.zhihu.com/question/28518092
标签:加速度 size 变换 选择 解释 整理 文学 数学 重点
原文地址:http://www.cnblogs.com/edward-bian/p/7395968.html