标签：bsp   k-means   概率计算   2-2   穷举   col   防止   混合   不变性   

一、HMM建模

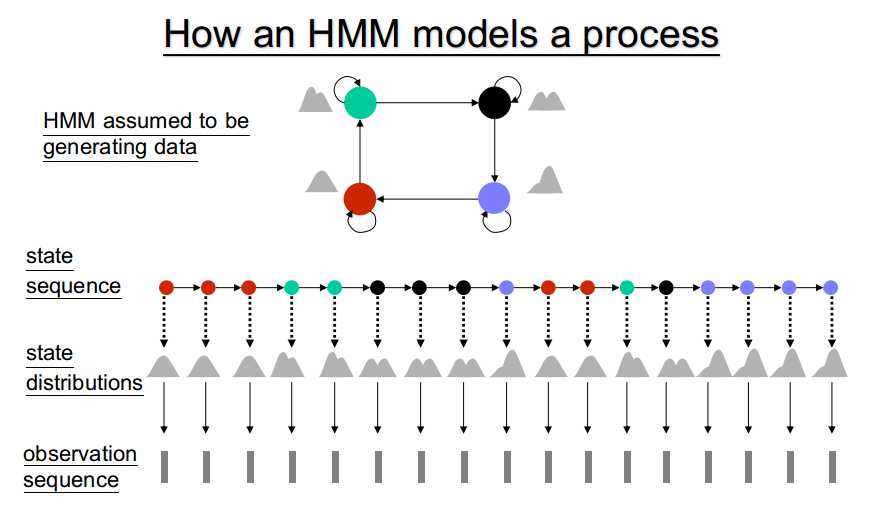
HMM参数：

二、HMM的３个假设

（一）马尔科夫假设

（二）观测独立性假设

（三）不变性假设

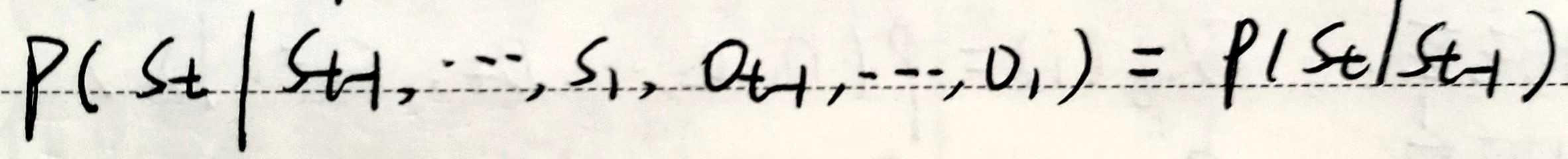
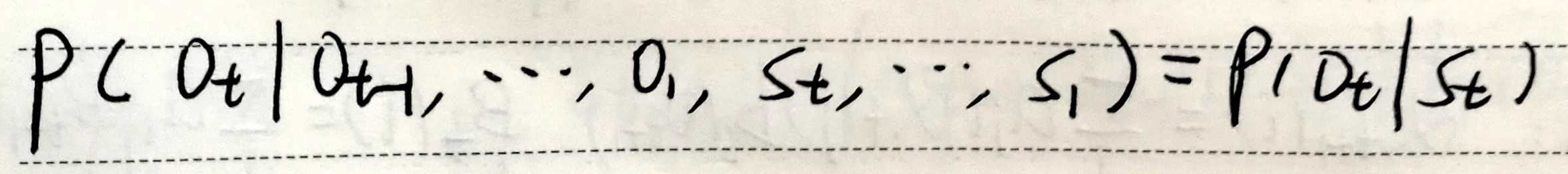
转移矩阵A不随时间变化

三、HMM的3个问题

（一）概率计算／评估－－－likelihood

给定模型参数以及观测序列，求当前模型参数下生成给定观测序列的概率。

1、穷举法

2、前向算法

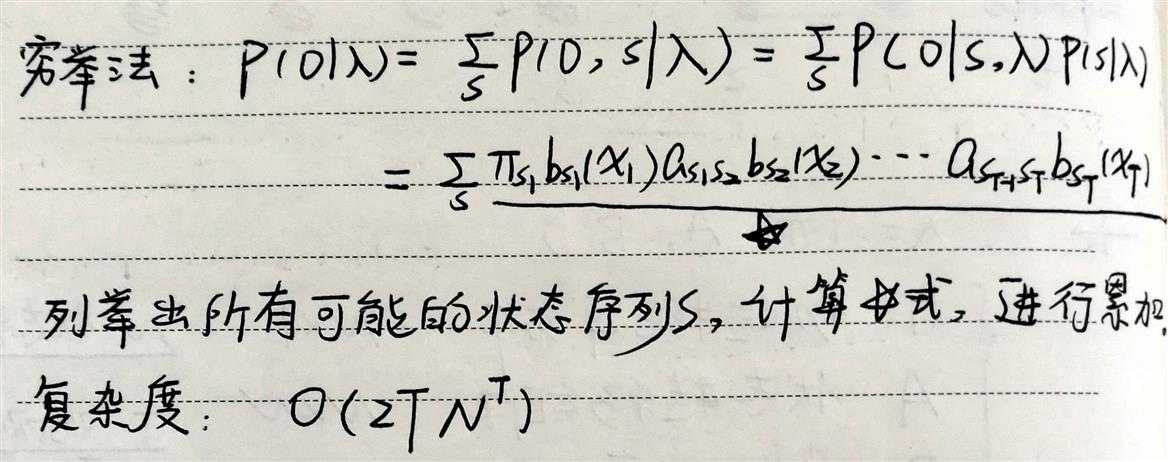
为了降低穷举法的计算复杂度。

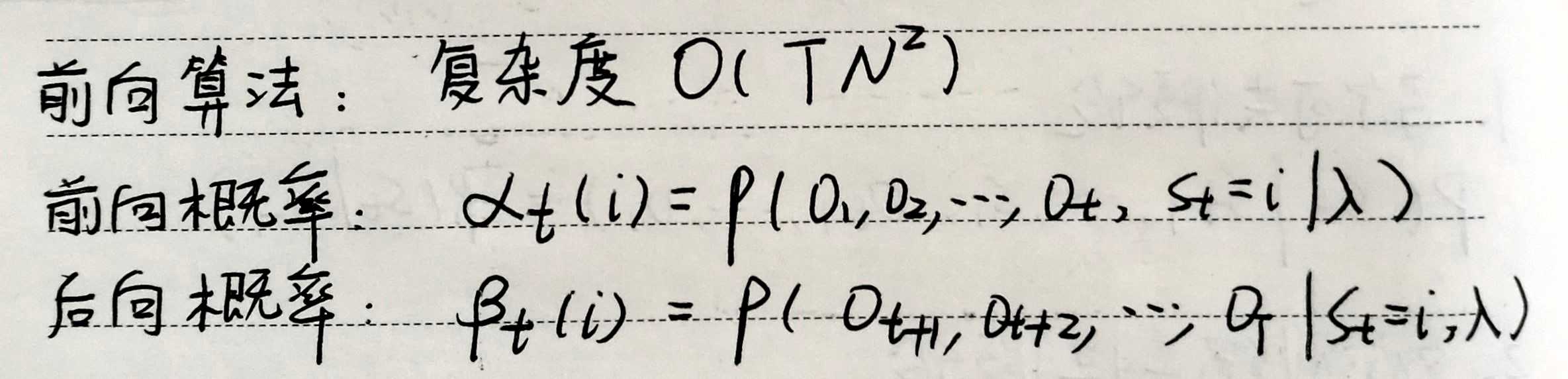
注：

在概率计算问题中，无需用到后向概率，

之所以计算后向概率，是为参数估计问题服务。

3、维特比近似

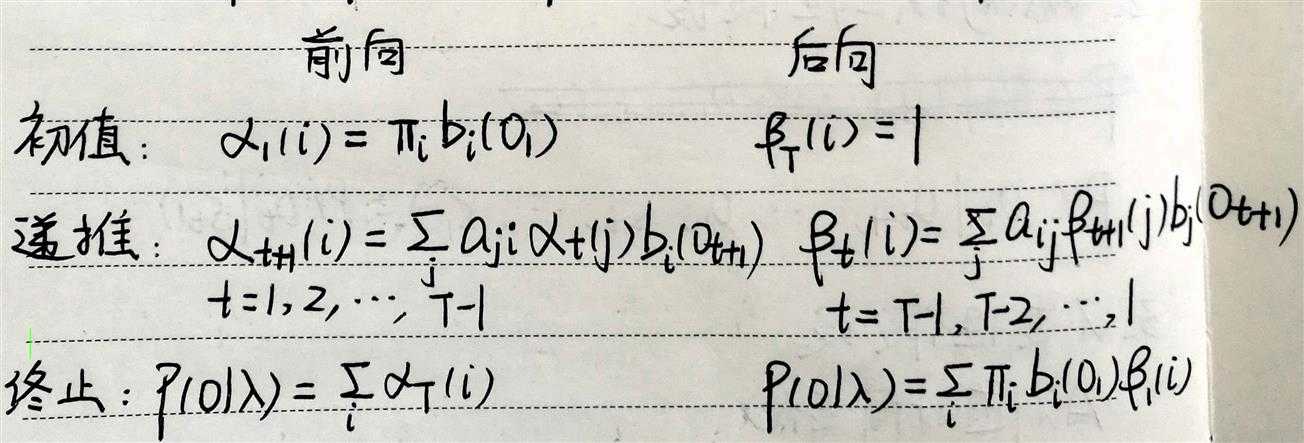
与穷举法，前向算法遍历所有可能的状态序列不同的是，

维特比近似使用最大概率状态序列代替所有可能的状态序列进行近似计算，

具体算法参见2)解码问题中的维特比算法。

（二）解码／状态分割－－－decoding

给定模型参数以及观测序列，求当前模型参数下，给定观测序列下，使得观测序列生成概率最大的状态序列。

1、近似算法

2、维特比算法

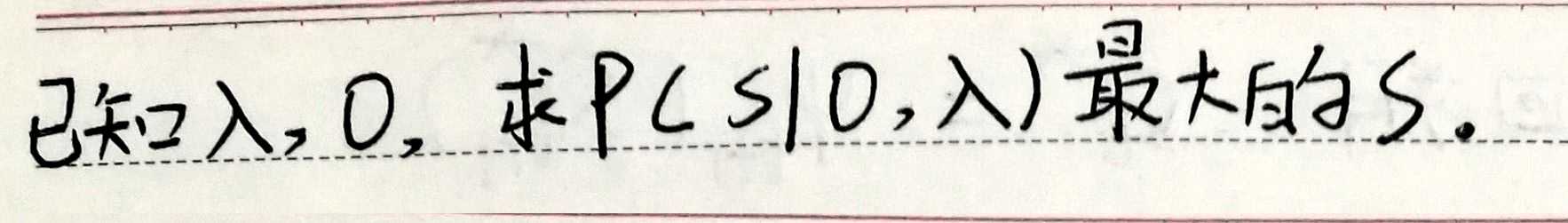
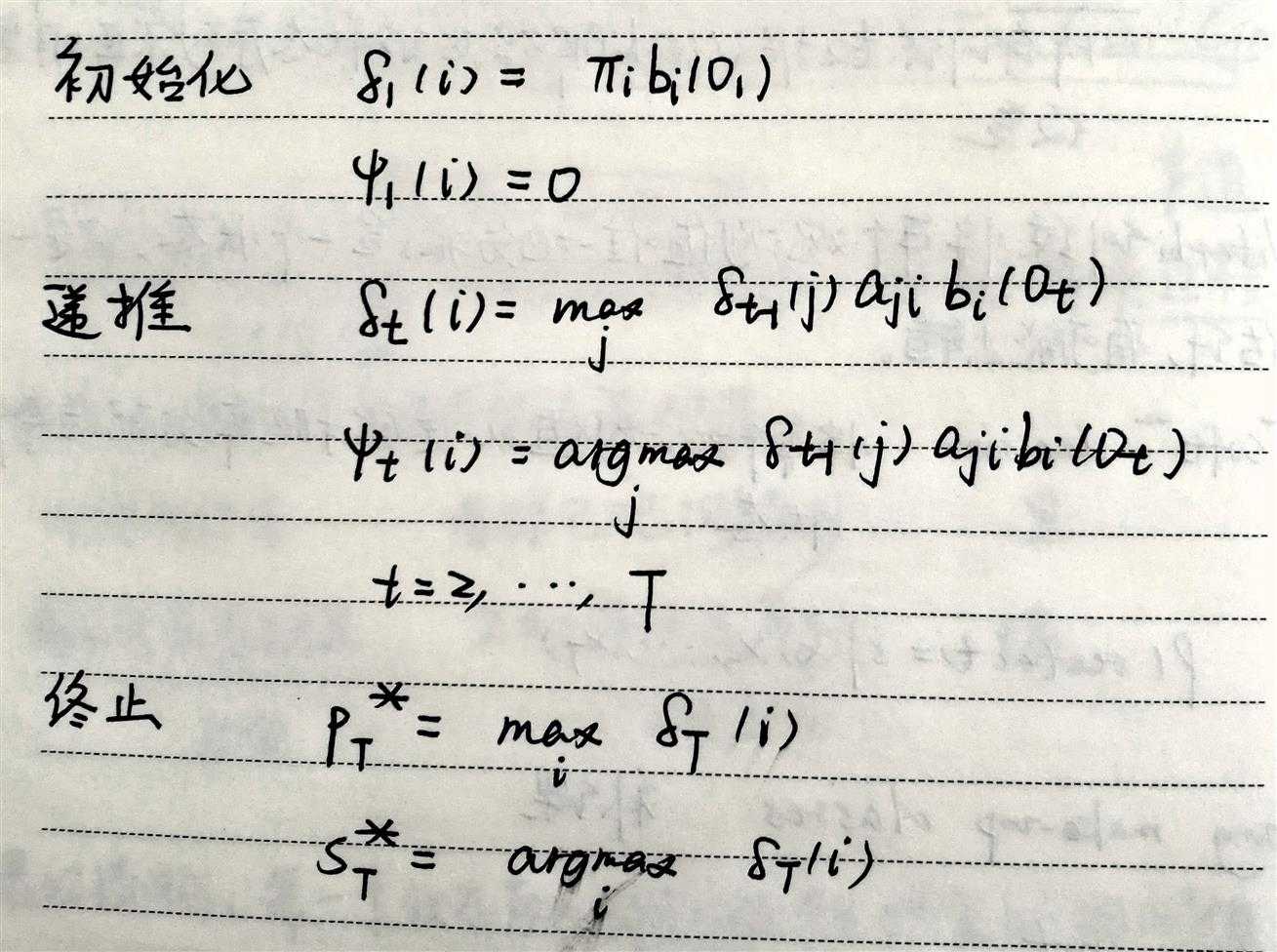
关于概率计算问题中的维特比近似：

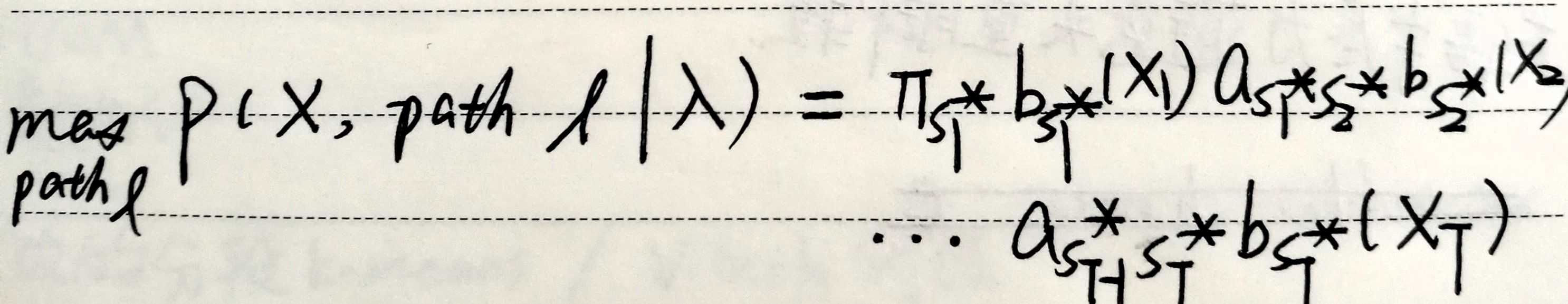
注意：

近似算法与维特比算法得到的状态路径常不同。

（三）参数估计－－－training

若观测序列和状态序列都已知，属于监督学习问题，应用MLE；

通常观测序列已知，状态序列未知，属于无监督学习问题，应用EM。

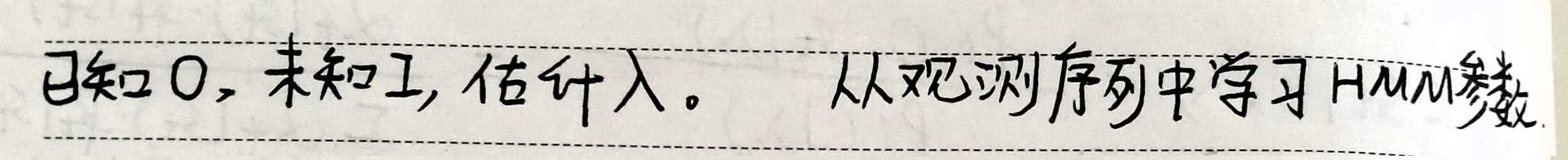
首先得确定HMM拓扑结构：

1、分段k-means／Viterbi训练

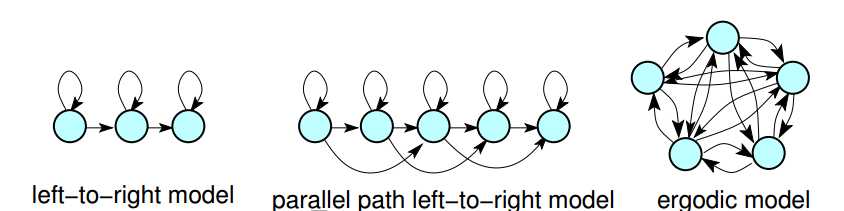
1）GSM-HMM

2）GMM-HMM

分裂高斯：

（1）通过加上或减去小数字调整均值；

（2）将原高斯分量权重一分为二，分给生成的高斯分量。

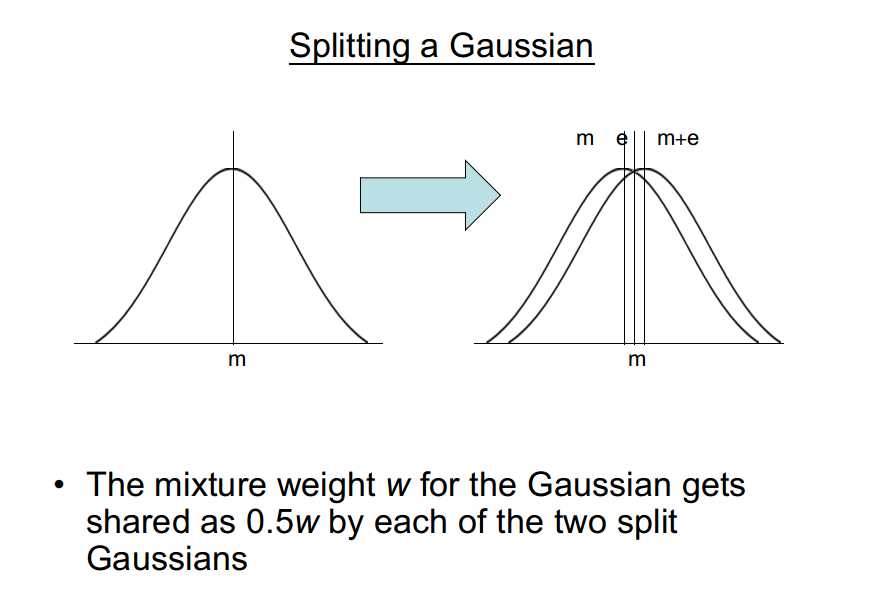
N个高斯分量变为N+1个高斯分量

维特比训练将每个观测值唯一地分配给一个状态：

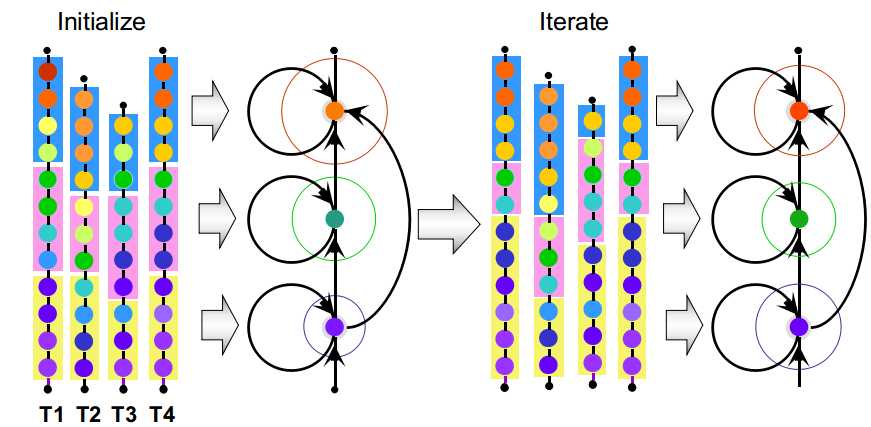
这只是一种估计，有可能会出错。

2、Baum Welch算法／前向后向算法

soft decision－－－将每个观测值以一定的概率分配给每个状态

1）GSM-HMM

E步：根据当前参数，计算下面２个统计量。

gamma：在t时刻占据状态j的概率。

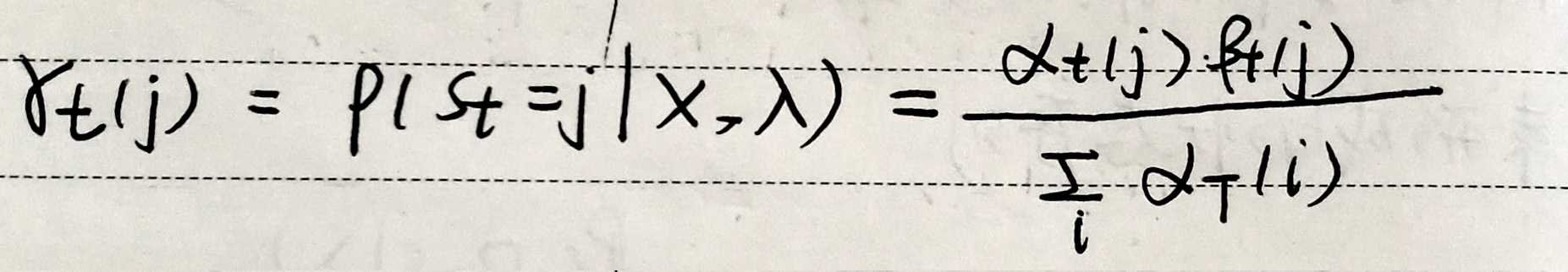
isu：在t时刻占据状态i，t+1时刻占据状态j的概率。

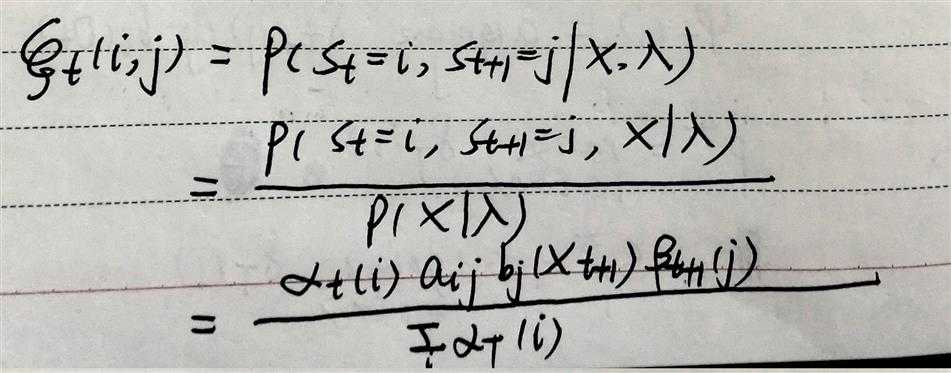
M步：

根据这２个状态占有概率，对模型参数进行更新，重新估计。

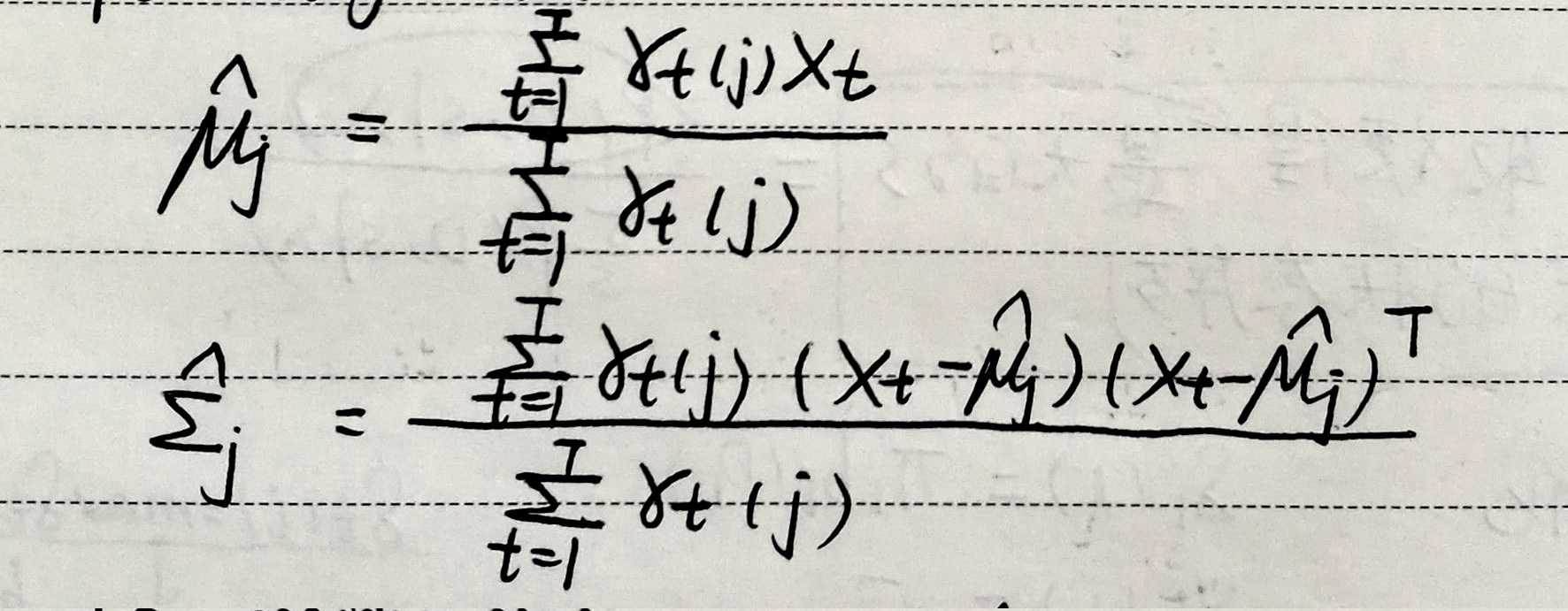
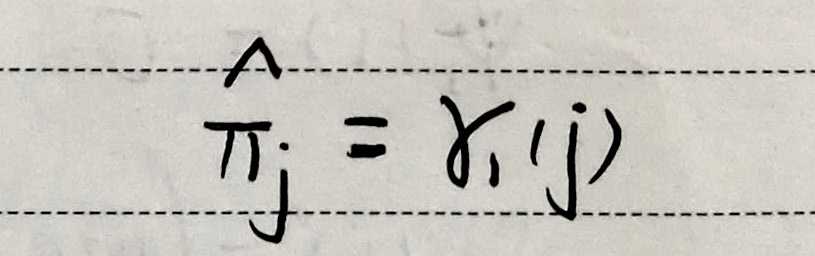
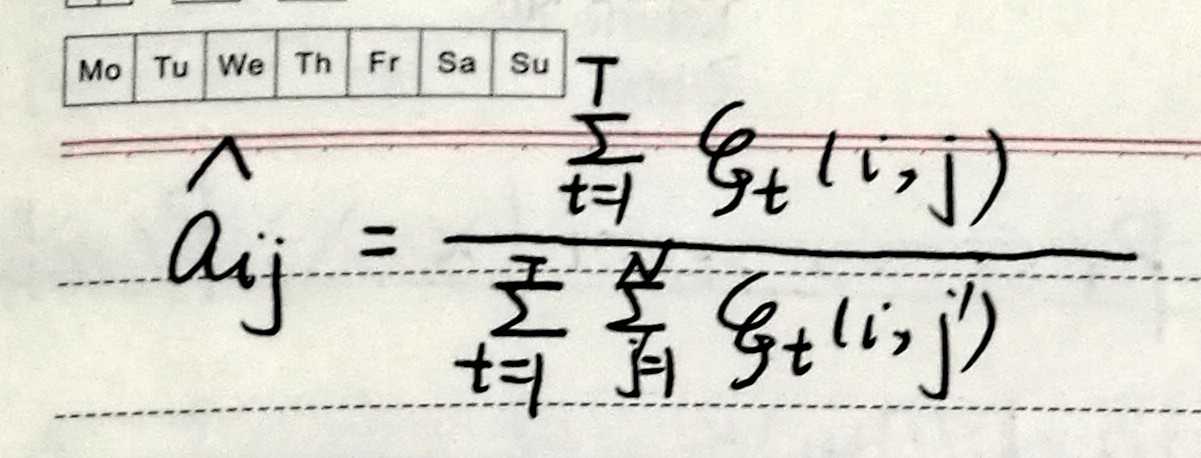
2）GMM-HMM

E步：根据当前参数，计算下面２个统计量。
gamma：在t时刻占据状态j的混合分量m的概率。

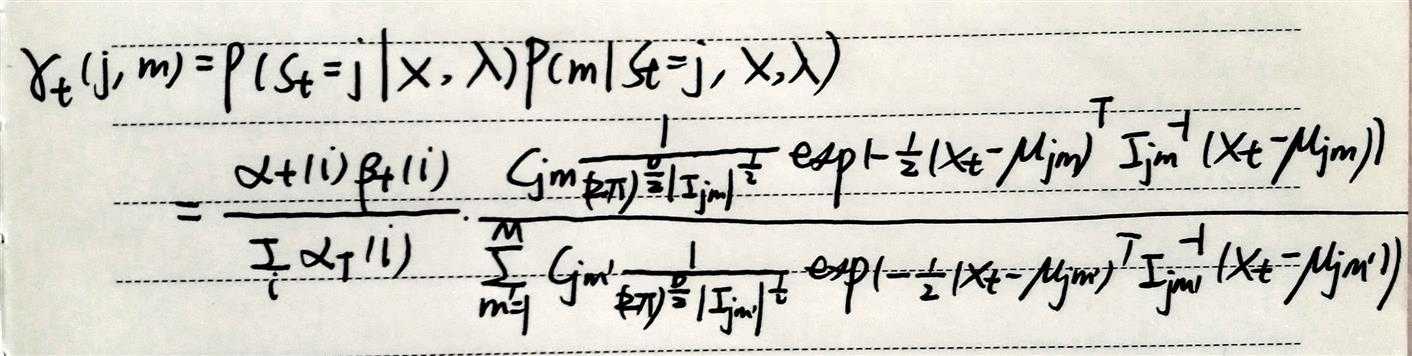
isu：在t时刻占据状态i，t+1时刻占据状态j的概率。

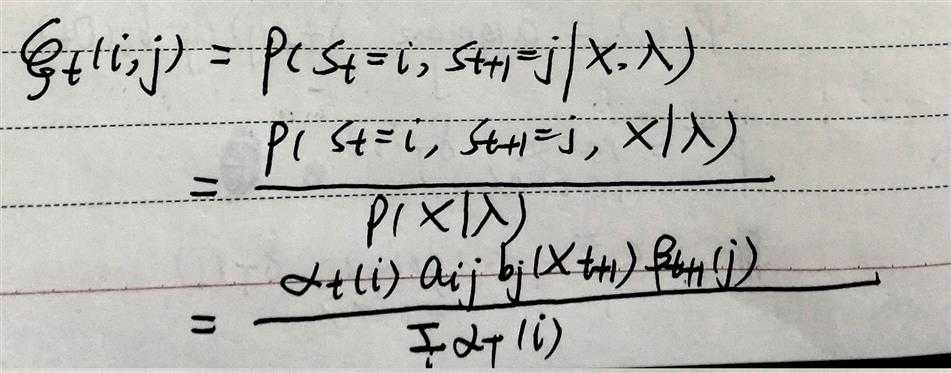
M步：

根据这２个状态占有概率，对模型参数进行更新，重新估计。

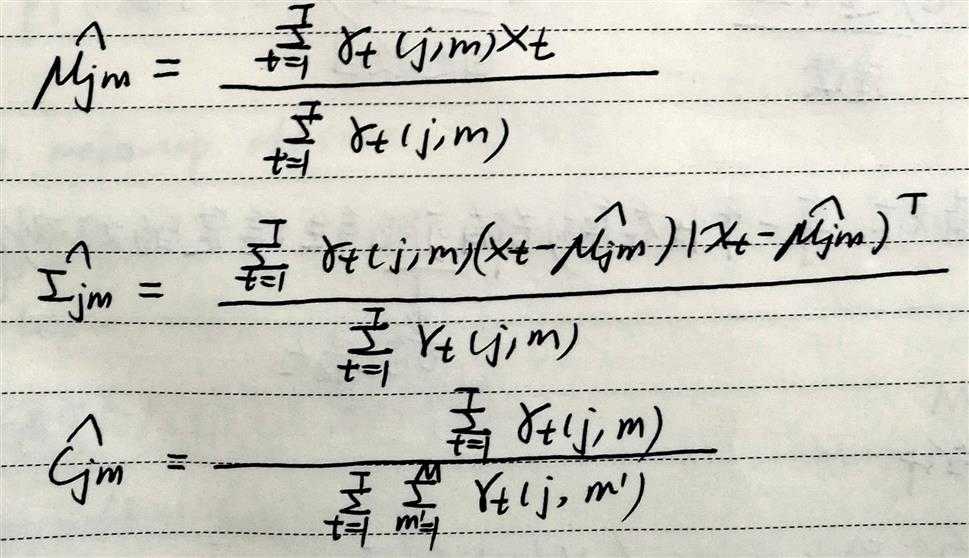
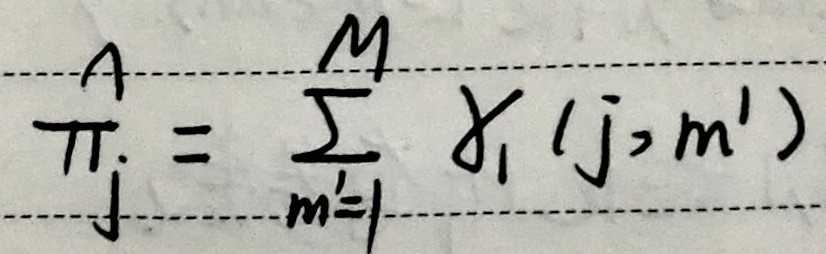
 注：

实现BW时为防止下溢（值趋近于0），

可对相应值进行适当的缩放，

可在对数域计算（乘法变为加法）。

HMM基础

标签：bsp   k-means   概率计算   2-2   穷举   col   防止   混合   不变性   

原文地址：http://www.cnblogs.com/cherrychenlee/p/6769370.html