标签:pre i++ blog bcd .com src dep color dfs



题意:
学过博弈论的同学都知道Nim游戏后手必胜的条件是异或和为0
给定一棵树 ,支持修改单点点权,询问链上异或和
预处理每个点到根的路径的异或和
由于异或的特殊性质,在求链x->y的异或和的时候,我们只需要知道x到根的异或和,y到根的异或和,将他们异或起来,最后异或上lca处的值即可。
如图,查询两个灰色节点的异或和
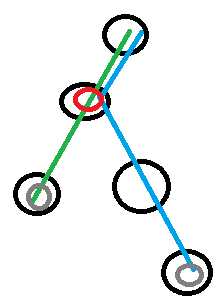
如果一个点的值被修改,那么它和它的子树到根的路径的异或和的值都会被修改
所以,我们维护一棵dfs序为下标的线段树,线段树的sum意义是它的区间的值的异或和
修改一个值,如果该值为x,要变成y,那么给线段树传进一个x^y的值,这样就能做到修改它和它的子树的值
因为一个数异或本身等于0,然后再异或y,就变成y了
修改的区间为dfs[x]~dfs[x]+size[x]-1
查询最近公共祖先我写的是树剖(常数小,又能顺便求dfs序)

#include<iostream> #include<cstdio> #include<cstring> using namespace std; int fa[500010],dep[500010],dfs[500010],top[500010],size[500010],son[500010],dfn=0; int to[1000100],next[1000100],h[500010],k=0;int a[500100],val[500010],n,m; int l[2000100],r[2000100],sum[2000100],lazy[2000100]; void ins(int u,int v){next[++k]=h[u];h[u]=k;to[k]=v;} void dfs1(int x,int d,int f) { dep[x]=d;fa[x]=f;size[x]=1; for(int i=h[x];i;i=next[i]) { if(to[i]==f)continue; dfs1(to[i],d+1,x);size[x]+=size[to[i]]; if(size[son[x]]<size[to[i]])son[x]=to[i]; } } void dfs2(int x,int tp) { top[x]=tp;dfs[x]=++dfn;a[dfs[x]]=a[dfs[fa[x]]]^val[x]; if(son[x])dfs2(son[x],tp); for(int i=h[x];i;i=next[i]) { if(to[i]==son[x]||to[i]==fa[x])continue; dfs2(to[i],to[i]); } } int lca(int u,int v) { while(top[u]!=top[v]) { if(dep[top[u]]<dep[top[v]])v=fa[top[v]]; else u=fa[top[u]]; } if(dep[u]<dep[v])return u; else return v; } void pushdown(int x) { if(!lazy[x])return; lazy[x<<1]^=lazy[x];lazy[x<<1|1]^=lazy[x]; sum[x<<1]^=lazy[x];sum[x<<1|1]^=lazy[x]; lazy[x]=0; } void pushup(int x) { sum[x]=sum[x<<1]^sum[x<<1|1]; } void build(int x,int L,int R) { l[x]=L;r[x]=R;lazy[x]=0;if(L==R){sum[x]=a[L];return;} build(x<<1,L,(L+R)/2);build(x<<1|1,(L+R)/2+1,R);pushup(x); } void add(int x,int L,int R,int k) { if(L==l[x]&&R==r[x]){lazy[x]^=k;sum[x]^=k;return;} pushdown(x);int mid=(l[x]+r[x])/2; if(R<=mid)add(x<<1,L,R,k); else if(L>mid)add(x<<1|1,L,R,k); else {add(x<<1,L,mid,k);add(x<<1|1,mid+1,R,k);} pushup(x); } int query(int x,int k) { if(l[x]==k&&r[x]==k){return sum[x];} pushdown(x);int mid=(l[x]+r[x])/2; if(k<=mid)return query(x<<1,k);else return query(x<<1|1,k); } int main() { freopen("game.in","r",stdin); freopen("game.out","w",stdout); scanf("%d",&n); for(int i=1;i<=n;i++)scanf("%d",&val[i]); for(int i=1;i<n;i++) { int x,y;scanf("%d%d",&x,&y);ins(x,y);ins(y,x); } dfs1(1,1,0);dfs2(1,1);build(1,1,n); scanf("%d",&m); for(int i=1;i<=m;i++) { char c[2];int x,y;scanf("%s%d%d",c,&x,&y); if(c[0]==‘C‘){add(1,dfs[x],dfs[x]+size[x]-1,val[x]^y);val[x]=y;} else { int ans=query(1,dfs[x])^query(1,dfs[y])^val[lca(x,y)]; puts(ans?"Yes":"No"); } } return 0; }



看到此题,首先想到的是文理分科的模型,但是这题比文理分科还简单
我们发现相邻的格子要选不同的东西才有额外收益,而文理分科是选相同的东西
我们可以把矩阵黑白染色,然后将一种颜色割到S和T表示的含义交换。
这样就满足了题目要求

#include<iostream> #include<cstdio> #include<queue> #include<cstring> using namespace std; const int INF=1999999999; int r,c,d; int n,m; struct data{ int next,to,cap; } g[2000000]; int iter[11000],h[11000],level[11000],k=1,head,tail,q[11000]; void add(int from,int to,int cap) { g[++k].next=h[from]; h[from]=k; g[k].to=to; g[k].cap=cap; g[++k].next=h[to]; h[to]=k; g[k].to=from; g[k].cap=0; } void bfs(int s) { memset(level,0,sizeof(level)); head=tail=0; q[tail++]=s; level[s]=1; while(head!=tail) { int u=q[head++]; for(int i=h[u]; i; i=g[i].next) { if(!level[g[i].to]&&g[i].cap) { level[g[i].to]=level[u]+1; q[tail++]=g[i].to; } } } } int dfs(int u,int t,int f) { if(u==t)return f; int used=0,w; for(int &i=iter[u]; i; i=g[i].next) { if(g[i].cap&&level[g[i].to]==level[u]+1) { w=f-used; w=dfs(g[i].to,t,min(w,g[i].cap)); if(w) { g[i].cap-=w; g[i^1].cap+=w; used+=w; if(used==f)return f; } } } return used; } int dinic(int s,int t) { int flow=0; for(;;) { for(int i=0; i<=n; i++)iter[i]=h[i]; bfs(s); if(!level[t])return flow; flow+=dfs(s,t,INF); } } int main() { freopen("city.in","r",stdin);freopen("city.out","w",stdout); int r,c;scanf("%d%d",&r,&c);n=r*c; int S=0,T=n+1,tot=0;n++; for(int i=1;i<=r;i++) for(int j=1;j<=c;j++) { int u;scanf("%d",&u);tot+=u; if(i%2==j%2)add(S,c*(i-1)+j,u); else add(c*(i-1)+j,T,u); } for(int i=1;i<=r;i++) for(int j=1;j<=c;j++) { int u;scanf("%d",&u);tot+=u; if(i%2==j%2)add(c*(i-1)+j,T,u); else add(S,c*(i-1)+j,u); } for(int i=1;i<=r-1;i++) for(int j=1;j<=c;j++) { int u;scanf("%d",&u);tot+=u; add(c*(i-1)+j,c*i+j,u); add(c*i+j,c*(i-1)+j,u); } for(int i=1;i<=r;i++) for(int j=1;j<=c-1;j++) { int u;scanf("%d",&u);tot+=u; add(c*(i-1)+j,c*(i-1)+j+1,u); add(c*(i-1)+j+1,c*(i-1)+j,u); } printf("%d",tot-dinic(S,T)); return 0; }



以下所有数组下标从0开始
我们先预处理出每个位置开始,下一个字母的位置。
即用next[i][j]表示从第i个位置开始,下一个字母j的位置(包括本身),不存在设为451,0对应a,1对应b……
注意next[452][0……25]=451,next[|S|][0……25]=451
考虑状压DP
用dp[S]表示S中字母组成的所有排列的最后位置的最大值
举个例子吧,S=13=1101,即acd三个字母组成的所有排列的最后位置的最大值
dp[S]=max(dp[S],next[dp[s^(1<<i)]+1][i]) (i∈S)dp[0]=-1;
用上面的那个例子,S=13=1101,则dp[S]=max(next[dp[12=1100]+1][0],next[dp[9=1001]+1][2],next[dp[5=0101]+1][3])
最后如果dp[1111……11]=451,则不是,否则是
时间复杂度O(2^n * n),发现无法通过n>21的数据
我们可以发现,最小长度至少为n*(n-1)+1 (当n=4时,即abcdabcdabcda)
而22*21+1>450,所以输出No

#include<iostream> #include<cstdio> #include<cstring> using namespace std; int dp[5000000],next[500][27],n; string a; int DP(int S) { if(S==0||dp[S]!=-1)return dp[S]; for(int i=0;i<n;i++) if((S>>i)&1)dp[S]=max(dp[S],next[DP(S^(1<<i))+1][i]); return dp[S]; } int main() { freopen("string.in","r",stdin);freopen("string.out","w",stdout); int T;scanf("%d",&T); while(T--) { memset(dp,-1,sizeof(dp));dp[0]=-1;memset(next,0,sizeof(next)); scanf("%d",&n);cin>>a;if(n>21){puts("NO");continue;} int m=a.size()-1; for(int i=0;i<n;i++)next[m+1][i]=451,next[452][i]=451; next[m][a[m]-‘a‘]=m; for(int i=m;i>=0;i--) { for(int j=0;j<n;j++)next[i][j]=next[i+1][j]; next[i][a[i]-‘a‘]=i; } if(DP((1<<n)-1)==451)puts("NO");else puts("YES"); } return 0; }
标签:pre i++ blog bcd .com src dep color dfs
原文地址:http://www.cnblogs.com/lher/p/7565248.html