Matlab 实现神经网络实例

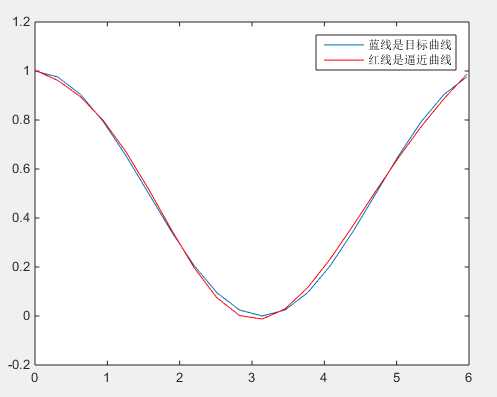
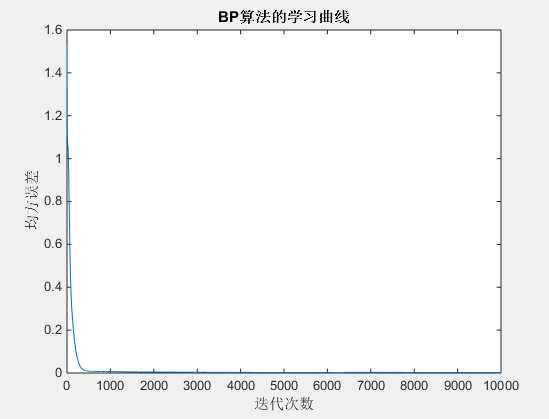
% Matlab实现简单BP神经网络 
% http://blog.csdn.net/zjccoder/article/details/40713147
    for i=1:20 %样本个数  
        xx(i)=2*pi*(i-1)/20;  
        d(i)=0.5*(1+cos(xx(i)));  
    end  
    n=length(xx);%样本个数  
    p=6; %隐层个数  
    w=rand(p,2);  
    wk=rand(1,p+1);  
    max_epoch=10000;%最大训练次数  
    error_goal=0.002;%均方误差  
    q=0.09;%学习速率  
    a(p+1)=-1;  
      
    %training  
    %此训练网络采取1-6-1的形式，即一个输入，6个隐层，1个输出  
    for epoch=1:max_epoch  
        e=0;  
        for i=1:n %样本个数  
            x=[xx(i);-1];   %按照行来连接，初始的输出都是-1，向着d(i)=0.5*(1+cos(xx(i))) 进行拟合
            neto=0;  
            for j=1:p   
                neti(j)=w(j,1)*x(1)+w(j,2)*x(2);  %w(j,1)输入层权值
                a(j)=1/(1+exp(-neti(j)));  
                %隐层的激活函数采取s函数，f(x)=1/(1+exp(-x))  
                neto=neto+wk(j)*a(j);  % 输出层wk(j)权值
            end            
            neto=neto+wk(p+1)*(-1);  %加上偏置
            y(i)=neto; %输出层的激活函数采取线性函数,f(x)=x  
            de=(1/2)*(d(i)-y(i))*(d(i)-y(i));  
            e=de+e;      
             %反向传播倒数第二层到输出层权值调整的量因为是线性激活函数，不需要求导
             %参考http://www.cnblogs.com/daniel-D/archive/2013/06/03/3116278.html
             %LMS算法
            dwk=q*(d(i)-y(i))*a;     
            for k=1:p  
                %(d(i)-y(i))*wk(k) 输出层的残差权值分配
                %a(k)*(1-a(k)为激活函数输出的倒数，
                %f(x) = 1/(1+exp(-x))    f‘(x) = f(x)(1-f(x)) = a(1-a)
                %x是当前层的输出，由于是第一层，输出和输入是相同的
                %参考blog.csdn.net/langb2014/article/details/46670901
                  dw(k,1:2)=q*(d(i)-y(i))*wk(k)*a(k)*(1-a(k))*x;  
            end     
            wk=wk+dwk; %从隐层到输出层权值的更新  
            w=w+dw; %从输入层到隐层的权值的更新      
        end   
        error(epoch)=e;  
        m(epoch)=epoch;      
        if(e<error_goal)              
           break;  
        elseif(epoch==max_epoch)  
            disp(‘在目前的迭代次数内不能逼近所给函数，请加大迭代次数‘)          
        end   
    end  
    %simulation  
    for i=1:n %样本个数  
        x=[xx(i);-1];    
        neto=0;  
        for j=1:p  
            neti(j)=w(j,1)*x(1)+w(j,2)*x(2);  
            a(j)=1/(1+exp(-neti(j)));  
            neto=neto+wk(j)*a(j);  
        end    
        neto=neto+wk(p+1)*(-1);  
        y(i)=neto; %线性函数  
    end   
      
    %plot  
    figure(1)  
    plot(m,error)  
    xlabel(‘迭代次数‘)  
    ylabel(‘均方误差‘)  
    title(‘BP算法的学习曲线‘)  
    figure(2)  
    plot(xx,d)  
    hold on  
    plot(xx,y,‘r‘)  
    legend(‘蓝线是目标曲线‘,‘红线是逼近曲线‘)