标签:set main 技术分享 ges pen logs long new [1]
学长终于良心出题了!
给学长打call!
————————————————我是分割线——————————————————
T1:超重(overweight)
【题目描述】
一天小D正在开飞机,当他吃完午饭,机舱里突然响起了警报声,原来是飞机超重了。小D当机立断,开始将机舱里的一些物品扔出窗外。小D的飞机里有n个物品,XY值分别为1~n,他希望扔掉尽量多的东西。但小D持有的两种强迫症让他迟迟无法下手:第一种是他希望所有扔掉的东西中,任意两个东西的XY值之和不是3的倍数;第二种是他有m个数字a1~am,任意一个扔掉的东西的XY值都不能被这m个数字中的任意一个整除。所以他把这个任务交给了担任僚机的你。
【输入数据】
第一行两个正整数n,m。
第二行m个数,表示小D拥有的数字。
【输出数据】
输出一个整数,表示小D最多能扔掉多少物品。
【样例输入】
4 1
1
【样例输出】
0
【数据范围】
对于10%的数据,n<=15;
对于30%的数据,n<=5*10^6;
另外10%的数据,m=0;
另外10%的数据,ai<m;
对于100%的数据,1<=n , ai<=5*10^8,0<=m<=15。
【样例解释】
因为1整除任何正整数,所以小D不能扔掉任何东西。
————————————————我是分割线——————————————————
显然我们只能取全部都是%3=1的数或者全部都是%3=2的数,如果有%3=0的数我们还能对答案+1
难度在与m的倍数不能取。
由于我们看到m非常的小,我们考虑容斥原理。
首先预处理出f[0],f[1],f[2]一开始有多少个,
然后我们直接暴力容斥就好啦!
下面贴代码
#include<cstdio> #define max(a,b) ((a)>(b)?(a):(b)) #define MN 16 #define ul unsigned long long using namespace std; int a[MN],qaq,f[3],n,m; ul res=0; long long chu(long long aa,int bb){return aa==0?aa:aa/bb;} long long gcd(long long aa,int bb){return bb==0?aa:gcd(bb,aa%bb);} long long lcm(long long aa,int bb){return aa*bb/gcd(aa,bb);} void dfs(ul res,int now,int sum,int goal,int cz){ if(sum==goal){ int qaq=res%3,tmp=chu(n/res,3); if(qaq==2){ f[0]+=cz*tmp; f[1]+=cz*(tmp+(n/res-tmp*3==2)); f[2]+=cz*(tmp+(n/res-tmp*3>=1)); }else if(qaq==1){ f[0]+=cz*tmp; f[1]+=cz*(tmp+(n/res-tmp*3>=1)); f[2]+=cz*(tmp+(n/res-tmp*3==2)); }else f[0]+=cz*(n/res); return; }else if(now==m+1)return; for(int i=now;i<=m;i++){ long long qqq=lcm(res,a[i]); if(qqq<=n)dfs(qqq,i+1,sum+1,goal,cz); } } int main(){ freopen("overweight.in","r",stdin); freopen("overweight.out","w",stdout); scanf("%d%d",&n,&m);f[0]=n/3,f[1]=n/3+(n-n/3*3>=1),f[2]=n/3+(n-n/3*3==2); for(int i=1;i<=m;i++)scanf("%d",&a[i]); for(int i=1;i<=m;i++) dfs(1,1,0,i,i%2?-1:1); printf("%d\n",max(f[1],f[2])+((f[0]>0)?1:0)); fclose(stdin); fclose(stdout); }
————————————————我是分割线——————————————————
T2:献祭(sacrifice)
【题目描述】
小C喜欢在他的n*m的棋盘上摆弄他的骑士们,每个格子上都有一个骑士,每个骑士有一个XY值vij。现在有人想掀翻他的棋盘用以献祭,小C当然不能苟同,他决定通过摆阵来吓傻对方。他希望留下若干个骑士,使得它们的XY值总和最大。但是处于阵法内的骑士会被施加一些没用的BUFF,每个骑士会攻击它们的控制区域。所以小C希望处于阵法中所有骑士互不攻击。
(一个骑士的控制区域为国际象棋中的“马”从该位置出发走一步能到的位置,如图所示:)
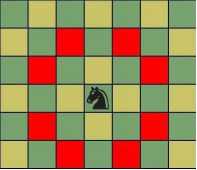
【输入数据】
第一行两个正整数n,m。
接下来n行,每行m个整数,表示每个格子上的骑士的XY值。
【输出数据】
输出一个整数,表示最终阵法最大的XY值总和。
【样例输入】
3 3
1 0 1
2 1 1
0 1 1
【样例输出】
5
【数据范围】
对于10%的数据,n*m<=15;
对于30%的数据,n*m<=300;
另外20%的数据,vij>0;
对于100%的数据,1<=n , m<=20000,n*m<=20000,|vij|<=20000。
【样例解释】
选取(2,1)、(2,2)、(2,3)、(3,2)四个格子上的骑士,2+1+1+1=5。
————————————————我是分割线——————————————————
黑白染色网络流,不解释。
#include<cstdio> #include<cstring> #define inf 0x3f3f3f3f #define min(a,b) ((a)<(b)?(a):(b)) #define MN 20005 using namespace std; int a[MN],level[MN],iter[MN],head[MN],num=1,n,m,que[MN],S,T,sum,tot,nx,ny; const int fx[8][2]={{-2,-1},{-2,1},{-1,-2},{-1,2},{1,-2},{1,2},{2,-1},{2,1}}; struct edge{ int to,next,w; }g[MN<<6]; bool spfa(){ memset(level,0,sizeof(level)); memcpy(iter,head,sizeof(head)); int h=1,t=1;que[1]=S;level[S]=1; while(h<=t){ int tmp=que[h++]; for(int i=head[tmp];i;i=g[i].next) if(level[g[i].to]==0&&g[i].w)level[g[i].to]=level[tmp]+1,que[++t]=g[i].to; }return level[T]!=0; } int dfs(int u,int flow){ if(u==T)return flow; int used=0; for(int &i=iter[u];i;i=g[i].next) if(level[g[i].to]==level[u]+1&&g[i].w){ int qaq=dfs(g[i].to,min(g[i].w,flow-used)); if(qaq){ g[i].w-=qaq,g[i^1].w+=qaq,used+=qaq; if(used==flow)return flow; } }return used; } int dinic(){ int tot=0,now; while(spfa())do now=dfs(S,inf),tot+=now;while(now); return tot; } void ins(int u,int v,int w){g[++num].next=head[u];head[u]=num;g[num].to=v;g[num].w=w;} void insw(int u,int v,int w){ins(u,v,w);ins(v,u,0);} void insw2(int u,int v){ins(u,v,inf);ins(v,u,inf);} inline bool check(int x,int y) {return x>=1&&x<=n&&y>=1&&y<=m;} int main(){ freopen("sacrifice.in","r",stdin); freopen("sacrifice.out","w",stdout); scanf("%d%d",&n,&m);S=0,T=n*m+1; for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)scanf("%d",&a[(i-1)*m+j]),sum+=a[(i-1)*m+j]>0?a[(i-1)*m+j]:0; for(int i=1;i<=n;i++){ for(int j=1;j<=m;j++){ if(a[(i-1)*m+j]>0) if(tot%2)insw(S,(i-1)*m+j,a[(i-1)*m+j]); else insw((i-1)*m+j,T,a[(i-1)*m+j]); tot++; } if(m%2==0)tot++; } for(int i=1;i<=n;i++) for(int j=1;j<=m;j++)if(i+j&1){ for(int k=1;k<=8;k++)if(check(nx=i+fx[k][0],ny=j+fx[k][1]))insw2((i-1)*m+j,(nx-1)*m+ny); } printf("%d\n",sum-dinic()); fclose(stdin); fclose(stdout); }
————————————————我是分割线——————————————————
T3:欲望(urge)
【题目描述】
小H养了n棵竹笋,每棵竹笋有一个XY值ai。n棵竹笋整齐地排在他家门口的盐地里。冬去春来,又到了万物发春的季节。这一天,小H被一群人逼着去传火,但小H不同意,就开始了逃亡的旅途。他跑到家门口,突然想采集一下门口的竹笋,于是他开始朝盐地走去。由于竹笋们很傲娇,第i棵竹笋会在ti时刻钻出地面,此前它都会一直藏于地下。小H于0时刻站在第1棵竹笋的左边,即0号位置。在每一时刻开始时他都会检测自己脚下是否有钻出地面的竹笋,如果有,则决定是否采摘该竹笋,检测、采摘不需要花费时间;接下来他要对自己下一秒的行动作出决定,他可以决定自己用这一秒的时间移动到下一棵竹笋的位置,或是原地不动,但小H不能往回走。小H有T秒时间在盐地进行如上操作,他希望最后采摘的竹笋的XY值总和最大。
【输入数据】
第一行两个正整数n,T。
第二行n个正整数ai,表示每棵竹笋的XY值。
第三行n个正整数ti,表示每棵竹笋何时会钻出地面。
【输出数据】
输出一个整数,表示最大的XY值总和。
【样例输入】
2 3
1 1
2 2
【样例输出】
1
【数据范围】
对于5%的数据,ti=0;
对于15%的数据,n , T<=100;
对于30%的数据,n , T<=10000;
另外20%的数据,ai=1;
对于100%的数据,1<=n<=5*10^5,0<=T , ti , |ai|<=10^9。
【样例解释】
小H只能采到第1个或第2个竹笋。
标签:set main 技术分享 ges pen logs long new [1]
原文地址:http://www.cnblogs.com/ghostfly233/p/7598035.html