机器学习--决策树

标签：替换   block   带来   目标   ges   性能提升   连续   src   算法   

基本流程:

　　决策树:

　　　　根结点:属性测试，包含样本全集

　　　　内部结点:属性测试，根据属性测试的结果被划分到子结点中

　　　　叶结点：决策结果

　　划分选择:如何选择最优划分属性。目标是结点的"纯度"越来越高

　　1.信息增益：

　　　　使用“信息熵”:

　　信息增益越大，意味使用属性a划分所获得的“纯度提升”越大。因此可以使用信息增益进行决策树的划分属性选择。即在决策树算法的图中的第八行选择属性a*=argmaxGain(D,a)

　　2.增益率

　　Gain_ratio(D,a)=Gain(D,a)/IV(a)

　　IV(a)=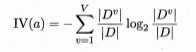

　　3.基尼指数

　　数据集的纯度可用基尼值来度量

　　剪枝:

　　如果能为决策树带来泛化性能提升，则将该子树替换为叶结点。

　　预剪枝，后剪枝

　　连续与缺失值

　　二分法、

机器学习--决策树

标签：替换   block   带来   目标   ges   性能提升   连续   src   算法   

原文地址：http://www.cnblogs.com/Ccmr/p/7598021.html