标签:back 通过 vector ... 下标 ges put div get
一、题目链接
http://codeforces.com/problemset/problem/591/C
二、题意
给定一个只含数字0和1的数组,通过如下方式,变成不再变化的01组合,最少需要操作几次。并输出最后得到的“稳定”01串。
操作方式:数组开头和结尾两个数不变,对于不是开头和结尾的数字a[i],a[i] = (a[i - 1], a[i], a[i + 1])三个数的中位数。
比如:1 0 1 0 1 0 1
一次:1 1 0 1 0 1 1
两次:1 1 1 1 1 1 1
输出:2
1 1 1 1 1 1 1
三、思路
1、这题纯属找规律题,对于连续一排(两个及以上)的0或1,无论怎么变,都和原来一样。
2、对于101010......这种组合:
(1)如果长度为奇数,则通过若干次操作后可使这一段变为和开头元素一样。即开头和结尾是0,则通过若干次操作后这段序列变成000……000,如果开头和结尾是1,则通过若干次操作后这段序列变成111……111。
(2)如果长度为偶数,如果头是0、尾是1,则通过若干次操作后这段变成前一半是0,后一半是1;如果头是1、尾是0,则通过若干次操作后这段变成前一半是1,后一半是0。
3、对于操作次数的问题,可以打表找到规律如下。
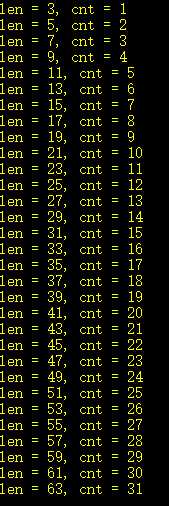
4、可以发现,当长度为2n + 1时(头尾是0和头尾是1是一样的),需要操作的次数为n。同理,当长度为2n时(头尾为0……1和头尾为1……0是一样的),需要操作的次数为n - 1。
5、找到规律后,遍历一次数字串,记录满足01交叉的子串的起始和末尾下标。然后遍历所有满足01交叉的子串,使用上述规律,记录操作次数的最大值即为结果的第一部分。同时,对该子串使用上述规律做替换,然后输出整个序列即可。
四、正确性证明
如果某段a[i], a[i + 1], ……,a[j]子串满足01交叉,len = j - i + 1:
1、如果len为奇数,不妨假设为1010……101,则a[i - 1]和a[j + 1]必为1(不然还可以更长),因为串头和串尾是不变的,而且每操作一次,最靠近开头和结尾的0就会变成1,所以,这段子串必然要经过上述的规律次数才能变成“稳定”串(因为没人可以帮它,它也不能帮别人)。所以上述找规律的操作对于每一段满足01交叉的子串都是独立的,不会相互影响。同理,0101……010这样的子串道理也是一样的。
2、如果len为偶数,不妨假设为1010……10,则a[i - 1]必为1,a[j + 1]必为0(不然还可以更长),然后证明过程和上述一样了。
五、源代码
#include<bits/stdc++.h>
using namespace std;
int n;
int a[500010];
typedef pair<int, int> PII;
vector<PII> vec;
int main() {
#ifndef ONLINE_JUDGE
freopen("input.txt", "r", stdin);
#endif // ONLINE_JUDGE
int s, t;
while(~scanf("%d", &n)) {
vec.clear();
for(int i = 1; i <= n; ++i)scanf("%d", a + i);
for(int i = 2; i <= n; ++i) {
if(a[i] ^ a[i - 1]) {
for(s = i - 1; i <= n && a[i] ^ a[i - 1]; ++i);
t = i;
vec.push_back(make_pair(s, t));
}
}
int ans = 0;
for(int i = 0, sz = vec.size(); i < sz; ++i) {
PII& p = vec[i];
int len = p.second - p.first;
if(len % 2 == 1) {
ans = max(ans, (len - 1) / 2);//len为奇数,len / 2 == (len - 1) / 2。
for(int k = p.first; k < p.second; ++k)a[k] = a[p.first];
} else {
ans = max(ans, (len - 1) / 2);
for(int k = p.first; k < p.first + len / 2; ++k)a[k] = a[p.first];
for(int k = p.first + len / 2; k < p.second; ++k)a[k] = a[p.second - 1];
}
}
printf("%d\n", ans);
for(int i = 1;i <= n;++i)printf("%d%c", a[i], i < n ? ‘ ‘ : ‘\n‘);
}
return 0;
}
六、附:找规律程序源代码(注意体会二进制的思想)
#include<bits/stdc++.h>
using namespace std;
int bit(long long& a, int x) {
return (a >> x) & 1;
}
int main() {
for(int i = 3; i <= 63; i += 2) {
long long a = 0, b = 0;
for(int j = 1; j < i; j += 2)a |= 1LL << j;
int cnt = 0;
while(a != 0 && a != (1LL << i) - 1) {
b = a;
for(int j = 1; j < i - 1; ++j) {
if(bit(a, j - 1) == bit(a, j + 1) && bit(a, j - 1) == 1)b |= (1LL << j);
if(bit(a, j - 1) == bit(a, j + 1) && bit(a, j - 1) == 0)b &= ~(1LL << j);
}
a = b;
++cnt;
}
printf("len = %d, cnt = %d\n", i, cnt);
}
return 0;
}
标签:back 通过 vector ... 下标 ges put div get
原文地址:http://www.cnblogs.com/565261641-fzh/p/7599267.html